如何解决TOP-K问题

前言：最近在开发一个功能:动态展示的订单数量排名前10的城市,这是一个典型的Top-k问题，其中k=10,也就是说找到一个集合中的前10名。实际生活中Top-K的问题非常广泛，比如：微博热搜的前100名、抖音直播的小时榜前50名、百度热搜的前10条、博客园点赞最多的blog前10名，等等如何解决这类问题呢？初步的想法是将这个数据集合排序,然后直接取前K个返回。这样解法可以，但是会存在一个问题：排序了很多不需要去排序的数据,时间复杂度过高.假设有数据100万,对这个集合进行排序需要很长的时间,即便使用快速排序,时间复杂度也是O(nlogn)，那么这个问题如何解决呢？解决方法就是以空间换时间,使用优先级队列

目录

一:  认识PriorityQueue
二：利用PriorityQueue解决topk问题
三：总结

一：认识PriorityQueue

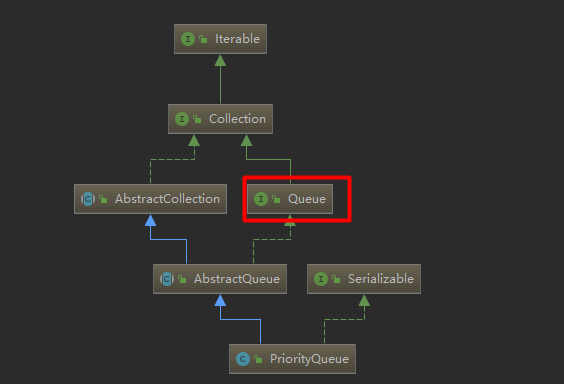
1.1：PriorityQueue位于java.util包下,继承自Collection,因此它具有集合的属性,并且继承自Queue队列,拥有add/offer/poll/peek等一系列操作元素的能力,它的默认大小是11,底层使用Object[] 来保存元素,数组的话肯定会有扩容,当添加元素的时候大小超过数组的容量,就会扩容，扩容的大小为原数组的大小加上,如果元素的数量小于64,则每次加2，如果大于64,则每次增加一半的容量。

 1.2：PriorityQueue的构造方法

    public PriorityQueue(Comparator<? super E> comparator) {
        this(DEFAULT_INITIAL_CAPACITY, comparator);
    }

 public PriorityQueue(int initialCapacity,
                         Comparator<? super E> comparator) {
        // Note: This restriction of at least one is not actually needed,
        // but continues for 1.5 compatibility
        if (initialCapacity < 1)
            throw new IllegalArgumentException();
        this.queue = new Object[initialCapacity];
        this.comparator = comparator;
    }

比较常用的就是这两个构造方法，其中第一个构造方法中需要构造一个比较器,第二个构造方法添加初始容量和比较器,比较器可以自定义任何元素的优先级,按照需要增加元素的优先级展示

 1.3：PriorityQueue的常用API

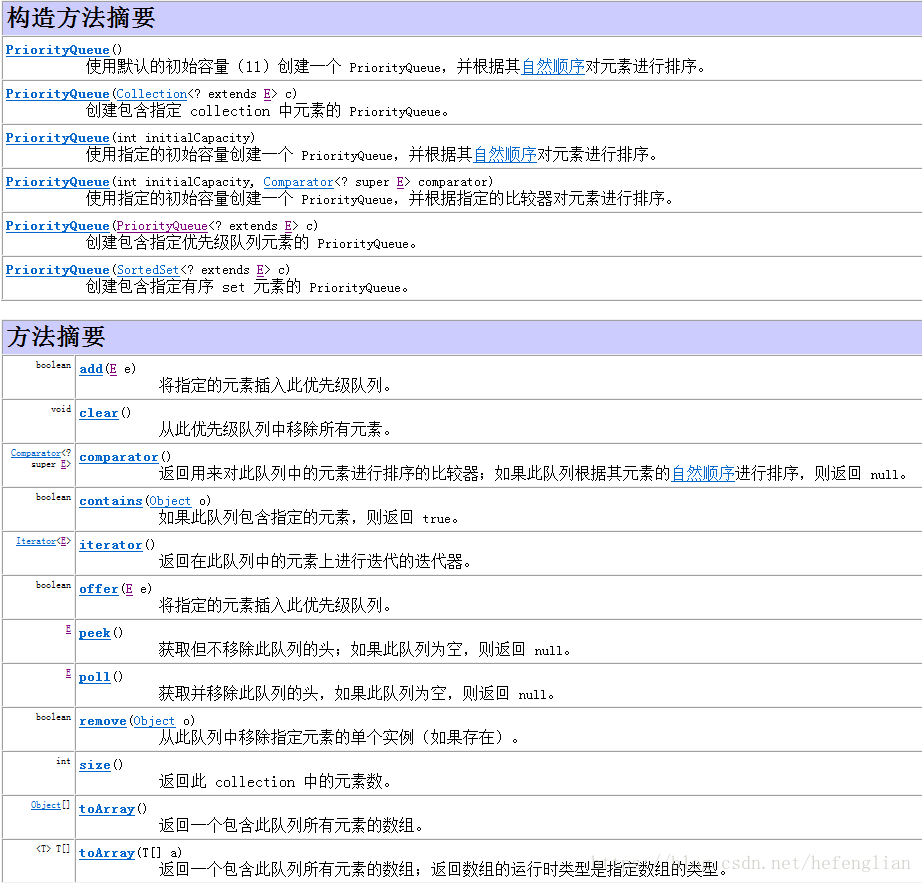
1.3.1：offer方法和add方法用于添加元素,本质上offer方法和add方法是相同的：

    public boolean add(E e) {
        return offer(e);
    }

 offer方法主要步骤就是判空、扩容、添加元素,添加元素的话,siftup方法里会根据构造方法,如果有比较器就进行比较,没有比较器的话就给元素赋予比较能力,并且根据构造的大小,也就是

 initialCapacity进行比较，如果比较器的compare方法不符合定义的规则,直接break;符合的话会给数组的元素进行赋值

public boolean offer(E e) {
        if (e == null)
            throw new NullPointerException();
        modCount++;
        int i = size;
        if (i >= queue.length)
            grow(i + 1);
        size = i + 1;
        if (i == 0)
            queue[0] = e;
        else
            siftUp(i, e);
        return true;
    }

1.3.2：poll方法和peek方法都是返回头元素,不同之处在于poll方法会返回头顶元素并且移除元素,peek方法不会移除头顶元素：

  public E poll() {
        if (size == 0)
            return null;
        int s = --size;
        modCount++;
        E result = (E) queue[0];
        E x = (E) queue[s];
        queue[s] = null;
        if (s != 0)
            siftDown(0, x);
        return result;
    }

    public E peek() {
        return (size == 0) ? null : (E) queue[0];
    }

 二：PriorityQueue解决问题

2.1：数组的前K大值

代码：

import java.util.PriorityQueue;

public class TopK {

    //找出前k个最大数，采用小顶堆实现
    public static int[] findKMax(int[] nums, int k) {

        PriorityQueue<Integer> pq = new PriorityQueue<>(k);//队列默认自然顺序排列，小顶堆，不必重写compare

        for (int num : nums) {
            if (pq.size() < k) {
                pq.offer(num);
                //如果堆顶元素 < 新数，则删除堆顶，加入新数入堆,保持堆中存储着大值
            } else if (pq.peek() < num) {
                pq.poll();
                pq.offer(num);
            }
        }

        int[] result = new int[k];
        for (int i = 0; i < k && !pq.isEmpty(); i++) {
            result[i] = pq.poll();
        }
        return result;
    }
}

 测试：

 public static void main(String[] args) {
        int[] arr = new int[]{1, 6, 2, 3, 5, 4, 8, 7, 9};
        System.out.println(Arrays.toString(findKMax(arr, 3)));
    }

//输出：

优先级队列是如何解决这个问题的呢？

PriorityQueue默认是小顶堆，那么什么是小顶堆？什么是大顶堆？假设有3、7、8三个数，需要存储在优先级队列里,画个图大家理解下：

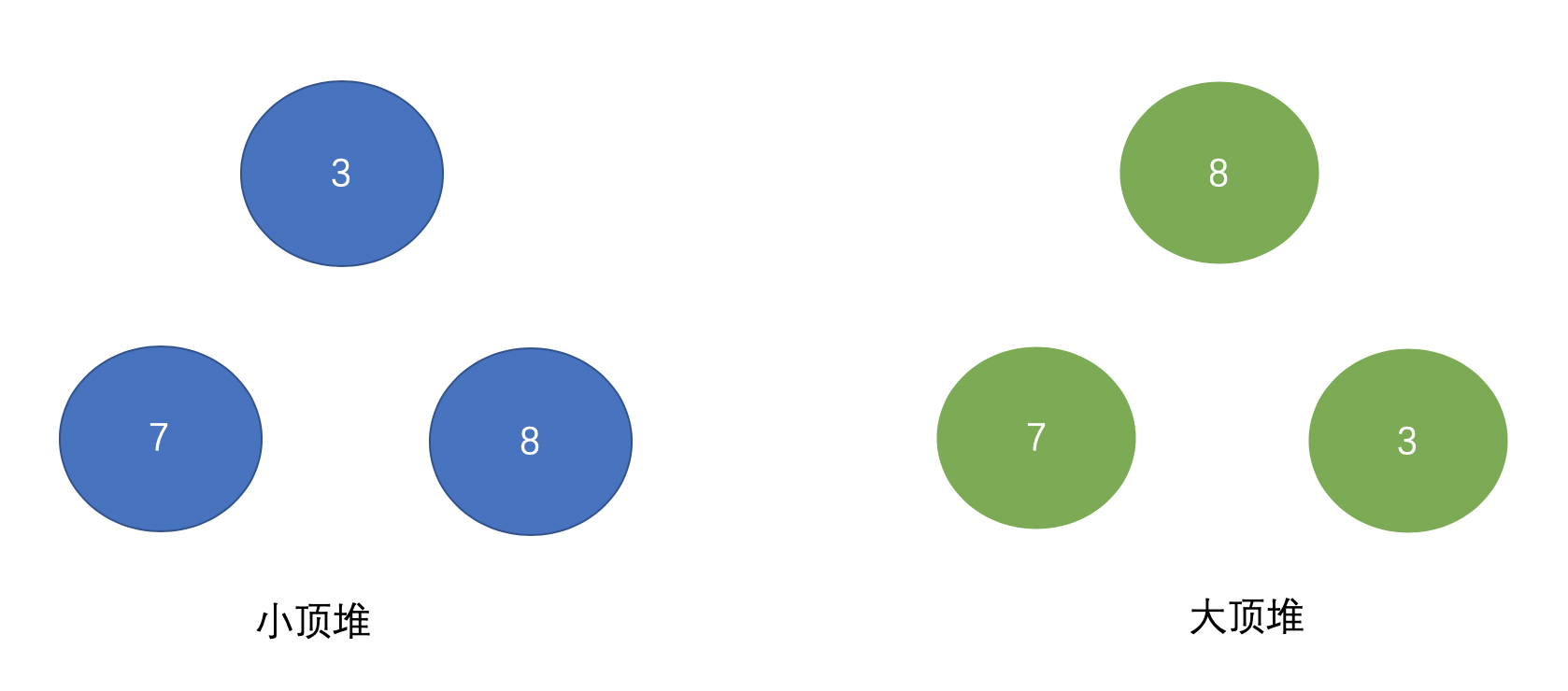
 可以看出小顶堆的头顶元素存储着整个数据集合中数字最小的元素，而大顶堆存储着整个数据集合中数字最大的元素,也就是一个按照升序排列，一个按照降序排列:

//小顶堆的构建方法：
PriorityQueue<Integer> queue = new PriorityQueue<>(k);
//这种写法等价于： 
PriorityQueue<Integer> queue = new PriorityQueue<>(k, new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o1-o2;
            }
        });
//同时等价于（lamda表达式的写法）
PriorityQueue<Integer> queue = new PriorityQueue<>(k, (o1, o2) -> o1-o2);

 //大顶堆的构建方法:
 PriorityQueue<Integer> queue = new PriorityQueue<>(k, new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o2-o1;
            }
        });

拿测试用例这个例子来说：

构建的是指定容量的小顶堆,因此每次queue.peek()返回的是最小的数字,在遍历数组的过程中，如果遇到比该数字大的元素就将最小的数字poll(移除掉),然后将较大的元素添加到堆中，在添加进去堆中的时候，堆同时会按照优先级比较，将最小的元素再次放到堆顶，这样的做法就是会一直保持堆中的元素是相对较大的,同时堆顶元素是堆中最小的。

按照测试用例给出的例子,{1, 6, 2, 3, 5, 4, 8, 7, 9} 优先级队列将会是这样转变的：(注意：本质上优先级队列的实现方式是数组,这里只是用二叉树的方式表现出来)

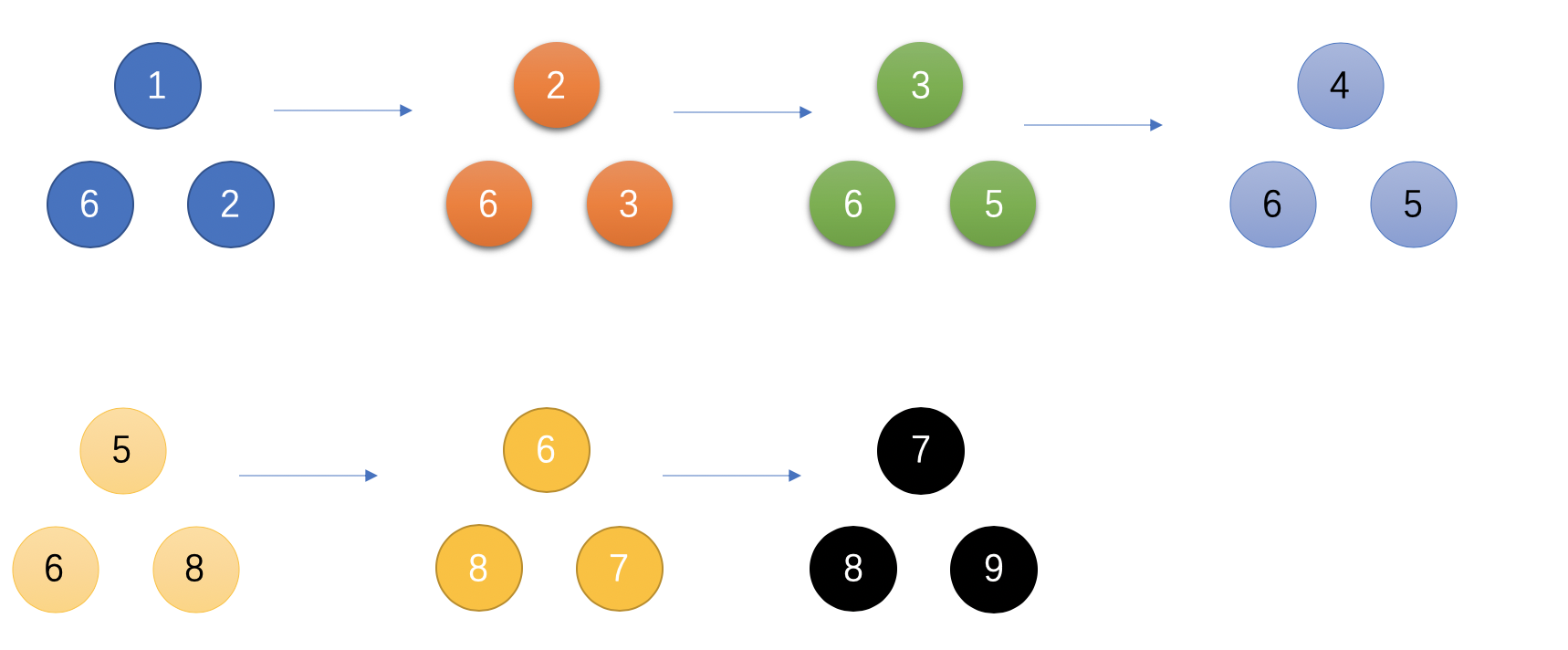
 假如该题换个角度,求出现频率最低的元素怎么做呢？

相信你根据上面的讲述应该也明白了：直接构建一个大顶堆，这样元素最大的值在堆顶,每次去和数组的元素的值去做比较，只要堆顶元素比数组的值小，就将堆顶元素poll出来，然后将数组的值添加进去，这样就可以一直保持集合数组中一直是最小的k个数字。

 2.2：前k个高频元素

当k = 1 时问题很简单，线性时间内就可以解决,只需要用哈希表维护元素出现频率，每一步更新最高频元素即可。当 k > 1 就需要一个能够根据出现频率快速获取元素的数据结构，这里就需要用到优先队列

首先建立一个元素值对应出现频率的哈希表，使用 HashMap来统计,然后构建优先级队列,这里依旧是构建小顶堆,不过因为该题是计算元素出现的频率,因此我们需要将每个元素的频率值做对比，

需要重写优先级队列的comparator,需要手工填值:这个步骤需要 O(N)O(N) 时间其中 NN 是列表中元素个数。

第二步建立堆，堆中添加一个元素的复杂度是 O(log(k))O(log(k))，要进行 NN 次复杂度是 O(N)O(N)。

最后一步是输出结果，复杂度为 O(klog(k))O(klog(k)):

public int[] topK(int[] nums, int k) {
        //统计字符出现的频率的map
        Map<Integer, Integer> count = new HashMap();
        for (int num : nums) {
            count.put(num, count.getOrDefault(num, 0) + 1);
        }

        //根据出现频率的map来构建k个元素的优先级队列
        PriorityQueue<Integer> heap =
                new PriorityQueue<>(k, (o1, o2) -> count.get(o1) - count.get(o2));

        for (int n : count.keySet()) {
            heap.add(n);
            if (heap.size() > k)
                heap.poll();
        }

        int[] result = new int[heap.size()];
        for (int i = 0; i < result.length; i++) {
            result[i] = heap.poll();
        }
        return result;

    }

 测试：

public static void main(String[] args) {
        int[] nums = {1, 1, 1, 3, 5, 6, 5, 6, 5, 4, 7, 8};
        int[] res = new TOPK().topK(nums, 3);
        System.out.println(Arrays.toString(res));
    }

//输出

  对于这样的问题需要先对原数组进行处理,比如在计算前3频率这个问题上,我们需要先计算数组中数字出现的频率，然后维护一个哈希表用来存储元素的频率。对于类似问题：微博热搜的前10名，那么肯定需要统计搜索频次，抖音小时榜前10名，那么肯定要统计要计算时段的观看人数，优先队列只不过是一个存储K元素的一个容器，它不负责统计，只负责维护一个K元素的最大或者最小堆顶，对于数据采用什么样的优先级顺序需要自定义。

如果用一句话来总结top-k问题：小顶堆用来求最大值,堆顶保存着最小值,判断如果堆顶的元素小于待遍历数组的元素，把当前元素poll出去，然后把待遍历数组元素添加进去;大顶堆用来求最小值,堆顶保存着最大元素,如果堆顶元素大于待遍历数组的值，就把当前元素poll出去，把待遍历数组的元素添加进去,这便是优先级队列的精髓。

三：总结

      本篇博客主要介绍了我们在实际中遇见的TOP-K问题有哪些，以及优先级队列PriorityQueue的基本原理介绍，接着由易到难的讲解了如何通过优先级队列PriorityQueue来解决TOP-k问题，这两个问题都比较经典。对于理解优先级队列的含义、以及为什么它能解决该问题，想明白这点很重要。希望大家能够做到举一反三，下次面对同等问题的时候，能顺序解决。起码棘手的topk问题对于我们来说，有个PriorityQueue这个神兵利器，就显得很简单easy咯。

最后: 如果对学习java有兴趣可以加入群:618626589,本群旨在打造无培训广告、无闲聊扯皮、无注水斗图的纯技术交流群，群里每天会分享有价值的问题和学习资料,欢迎各位随时加入～