14:27:28 写一首十几岁听的情歌,可惜我没在那个时候遇见你,否则我努力活到百岁以后,就刚好爱你一整个世纪 ——《零几年听的情歌》
今天是待在学校的最后一天了,撒花,庆祝!!!那也祝自己十六岁生日快乐
最近肺炎传染有点严重,大家能点外卖点外卖,能躺床躺床,少出门,你肆无忌惮赖在家的机会来了!!!
好了,今天要讲的呢,是要待在家好好学习一下的强连通分量。
-
概念
连通分量:在无向图中,即为连通子图。
有向图强连通分量:在有向图G中,如果两个顶点vi,vj间(vi>vj)有一条从vi到vj的有向路径,同时还有一条从vj到vi的有向路径,则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通,称G是一个强连通图。有向图的极大强连通子图,称为强连通分量(strongly connected components)
极大强连通子图:G是一个极大强连通子图,当且仅当G是一个强连通子图且不存在另一个强连通子图G’,是得G是G'的真子集
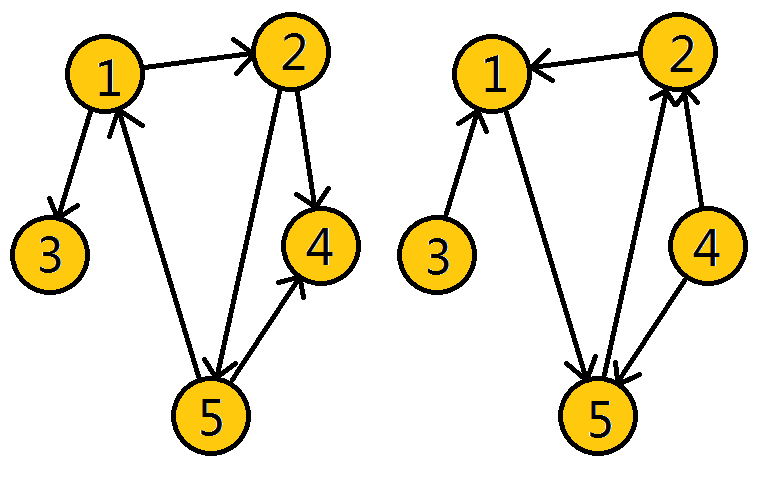
下图中,子图{1,2,3,4}为一个强连通分量,因为顶点1,2,3,4两两可达。{5},{6}也分别是两个强连通分量。

-
用双向遍历取交集的方法求强连通分量,时间复杂度为O(N^2+M)。
-
Kosaraju算法或Tarjan算法求强连通分量,两者的时间复杂度都是O(N+M)。
-
Tarjan算法
基于对图深度优先搜索,每个强连通分量为搜索树中的一棵子树。
算法流程
- 搜索时,把当前搜索树中未处理的节点加入一个堆栈
- 回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。
- 定义DFN(u)为节点u搜索的次序编号(时间戳),Low(u)为u或u的子树能够追溯到的最早的栈中节点的次序号。
- 当DFN(u)=Low(u)时,以u为根的搜索子树上所有节点是一个强连通分量。
以下为网上找的算法演示流程:
从节点1开始DFS,把遍历到的节点加入栈中。搜索到节点u=6时,DFN[6]=LOW[6],找到了一个强连通分量。退栈到u=v为止,{6}为一个强连通分量。
返回节点5,发现DFN[5]=LOW[5],退栈后{5}为一个强连通分量。
返回节点3,继续搜索到节点4,把4加入堆栈。发现节点4向节点1有后向边,节点1还在栈中,所以LOW[4]=1。节点6已经出栈,(4,6)是横叉边,返回3,(3,4)为树枝边,所以LOW[3]=LOW[4]=1。
继续回到节点1,最后访问节点2。访问边(2,4),4还在栈中,所以LOW[2]=DFN[4]=5。返回1后,发现DFN[1]=LOW[1],把栈中节点全部取出,组成一个连通分量{1,3,4,2}。
P1407 [国家集训队]稳定婚姻
此题需要用到一个map,就是类似于此。
map<string,int> a;、 for(int i=1;i<=n;i++) { string x,y; cin>>x>>y; a[x]=++tot;a[y]=++tot; }
因为需要存图,我在这里用的vector的邻接表,详细请看第三关。
这道题主要用到的就是targan算法,具体看代码,当然也有其他方法可以用
#include<bits/stdc++.h> using namespace std; int n,m,d[20009],tot,cnt,l[20009]; bool v[20009]; vector<int> f[8005]; map<string,int> a; stack<int> s; void tarjan(int x) { d[x]=l[x]=++cnt; v[x]=true; s.push(x); for(int i=0;i<f[x].size();++i) { int o=f[x][i]; if(!d[o]) { tarjan(o); l[x] =min(l[x], l[o]); } else if(v[o])l[x]=min(l[x],d[o]); } if(d[x]==l[x]) { v[x]=false; while(s.top()!=x) { v[s.top()]=false; s.pop(); } } } int main() { scanf("%d",&n); for(int i=1;i<=n;i++) { string x,y; cin>>x>>y; a[x]=++tot;a[y]=++tot; f[a[x]].push_back(a[y]); } scanf("%d",&m); for(int i=1;i<=m;i++) { string x,y; cin>>x>>y; f[a[y]].push_back(a[x]); } cnt = 0; for(int i=1;i<=n*2;i++) if(!d[i]) tarjan(i); cnt=0; for(int i=1;i<=n;i++) { if(l[++cnt]==l[++cnt]) printf("Unsafe "); else printf("Safe "); } return 0; }
-
Kosaraju算法
基于对有向图及其逆图两次DFS的方法Kosaraju算法可能会稍微更直观一些。但是Tarjan只用对原图进行一次DFS,不用建立逆图,更简洁。在实际的测试中,Tarjan算法的运行效率也比Kosaraju算法高30%左右。
算法流程:
- 先用对原图G进行深搜生成树
- 然后任选一棵树对其进行深搜(注意这次深搜节点A能往子节点B走的要求是EAB存在于反图GT)
- 能遍历到的顶点就是一个强连通分量
- 余下部分和原来的树一起组成一个新的树
- 直到没有顶点为止。
首先了解kosarajuo法,要想了解逆图
逆图(Tranpose Graph ):
我们对逆图定义如下:
GT=(V, ET),ET={(u, v):(v, u)∈E}}
以下为网上找的算法演示流程:

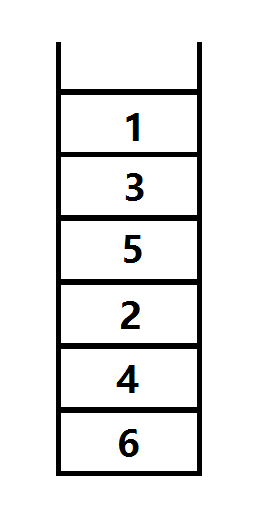
上图是对图G,进行一遍DFS的结果,每个节点有两个时间戳,即节点的发现时间u.d和完成时间u.f
我们将完成时间较大的,按大小加入堆栈
1)每次从栈顶取出元素
2)检查是否被访问过
3)若没被访问过,以该点为起点,对逆图进行深度优先遍历
4)否则返回第一步,直到栈空为止
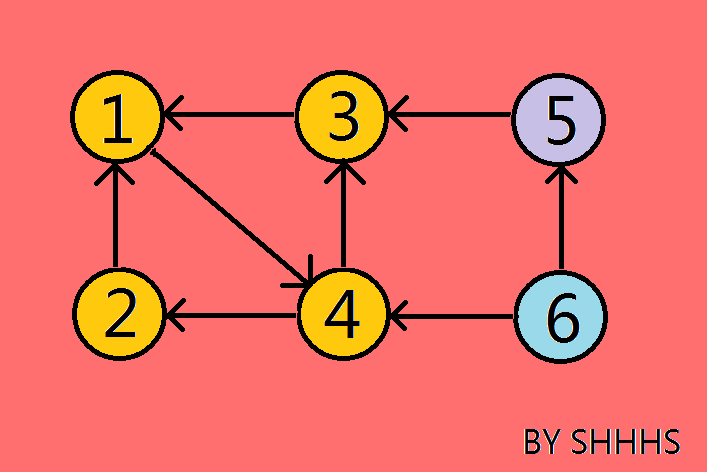
对逆图搜索时,从一个节点开始能搜索到的最大区块就是该点所在的强连通分量。
#include<bits/stdc++.h> using namespace std; const int maxn=1e6+5; struct edge{ int to,next; }edge1[maxn],edge2[maxn]; //edge1是原图,edge2是逆图 int head1[maxn],head2[maxn]; bool mark1[maxn],mark2[maxn]; int tot1,tot2; int cnt1,cnt2; int st[maxn];//对原图进行dfs,点的结束顺序从小到大排列。 int belong[maxn];//每个点属于哪个联通分量 int num;//每个联通分量的个数 int setnum[maxn];//每个联通分量中点的个数 void addedge(int u,int v){ edge1[tot1].to=v;edge1[tot1].next=head1[u];head1[u]=tot1++; edge2[tot2].to=u;edge2[tot2].next=head2[v];head2[v]=tot2++; } void dfs1(int u){ mark1[u]=true; for(int i=head1[u];i!=-1;i=edge1[i].next) if(!mark1[edge1[i].to]) dfs1(edge1[i].to); st[cnt1++]=u; } void dfs2(int u){ mark2[u]=true; num++; belong[u]=cnt2; for(int i=head2[u];i!=-1;i=edge2[i].next) if(!mark2[edge2[i].to]) dfs2(edge2[i].to); } void solve(int n){//点编号从1开始 memset(mark1,false,sizeof(mark1)); memset(mark2,false,sizeof(mark2)); cnt1=cnt2=0; for(int i=1;i<=n;i++) if(!mark1[i]) dfs1(i); for(int i=cnt1-1;i>=0;i--) if(!mark2[st[i]]){ num=0; dfs2(st[i]); setnum[cnt2++]=num; } } int main(){ int n,m; cin>>n>>m; for(int i=1;i<=m;i++){ int s,d; cin>>s>>d; addedge(s,d); } solve(1); return 0; }
P2002 消息扩散
其实kosaraju的复杂度和空间都要费的多一些
- 有自环
-
缩点,然后找入度为0的强连通分量个数就好了。对此,需要用mp1和mp2数组记录每条边连接的点最后遍历一遍所有的边
#include <bits/stdc++.h> using namespace std; const int maxn=1e5+5; const int maxx=5e5+5; vector<int>g[maxn],g2[maxn],st; bool vis[maxn]; int k,cmp[maxn],mp1[maxx],mp2[maxx],cnt,du[maxn]; int n,m; void dfs(int x){ vis[x]=1; for(int i=0;i<g[x].size();++i){ int s=g[x][i]; if(!vis[s]){ dfs(s); } } st.push_back(x); } void dfs2(int x,int k){ cmp[x]=k; vis[x]=1; for(int i=0;i<g2[x].size();++i){ int s=g2[x][i]; if(!vis[s]){ dfs2(s,k); } } } void init(){ for(int i=1;i<=n;i++){ if(!vis[i]) dfs(i); } for(int i=1;i<=n;i++){ vis[i]=0; } for(int i=st.size()-1;i>=0;i--){ if(!vis[st[i]]){ k++; dfs2(st[i],k); } } } int main(){ scanf("%d%d",&n,&m); for(int i=1;i<=m;++i){ int p1,p2; scanf("%d%d",&p1,&p2); cnt++; mp1[cnt]=p1;mp2[cnt]=p2; g[p1].push_back(p2); g2[p2].push_back(p1); } init(); for(int i=1;i<=cnt;i++){ int p1=mp1[i],p2=mp2[i]; if(cmp[p1]!=cmp[p2]){ // g[cmp[p1]].push_back(cmp[p2]); du[cmp[p2]]++; } } int ans=0; for(int i=1;i<=k;i++){ if(!du[i]) ans++; } printf("%d ",ans); return 0; }
-
缩点
定义:将有向图中的强连通分量缩成一个点。
在Targan算法与Kosaraju算法中有所体现
P2194 HXY烧情侣
这是一道Targan加缩点的题
vector数组记录每个联通块里的每一个点
最小汽油费即为每个联通块里最小点权
方案数即为每个联通块里最小点权的点数之积(乘法原理)%1e9+7
#include<bits/stdc++.h> #define N 501010 using namespace std; int n,head[N],tot,w[N],m,ans1,ans2=1; struct node { int to,next; } e[N]; void add(int u,int v) { e[++tot].to=v,e[tot].next=head[u],head[u]=tot; } const int mod=1e9+7; int dfn[N],low[N],item,b[N],a[N],cnt; bool vis[N]; stack<int>S; vector<int>g[N]; void tarjan(int u){ dfn[u]=low[u]=++item; S.push(u);vis[u]=1; for(int i=head[u];i;i=e[i].next){ int v=e[i].to; if(!dfn[v]){ tarjan(v); low[u]=min(low[u],low[v]); }else if(vis[v]) low[u]=min(low[u],dfn[v]); } if(low[u]==dfn[u]){ int v=u;++cnt; do{ v=S.top();S.pop(); vis[v]=0;b[v]=cnt;a[cnt]++; g[cnt].push_back(v); }while(v!=u); } } int main() { scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&w[i]); scanf("%d",&m); for(int a,b,i=1;i<=m;i++) { scanf("%d%d",&a,&b); add(a,b); } for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i); for(int i=1;i<=cnt;i++){ int tpt=g[i].size(),sby=0,mi=mod; for(int j=0;j<tpt;j++){ if(w[g[i][j]]<mi){ mi=w[g[i][j]]; sby=1; }else if(mi==w[g[i][j]]) ++sby; } ans1+=mi; ans2=(ans2%mod*sby%mod)%mod; } printf("%d %d",ans1,ans2); return 0; }
21:37:37 我们也学会慢慢地慢慢地推卸,我们也有过一次又一次的越界。——王巨星《越界》



