题目描述
一年一度的“幻影阁夏日品酒大会”隆重开幕了。大会包含品尝和趣味挑战 两个环节,分别向优胜者颁发“首席品酒家”和“首席猎手”两个奖项,吸引了众多品酒师参加。
在大会的晚餐上,调酒师 Rainbow 调制了 n 杯鸡尾酒。这 n 杯鸡尾酒排成一行,其中第 n 杯酒 (1 ≤ i ≤ n) 被贴上了一个标签si,每个标签都是 26 个小写 英文字母之一。设 str(l, r)表示第 l 杯酒到第 r 杯酒的 r − l + 1 个标签顺次连接构成的字符串。若 str(p, po) = str(q, qo),其中 1 ≤ p ≤ po ≤ n, 1 ≤ q ≤ qo ≤ n, p ≠ q, po − p + 1 = qo − q + 1 = r ,则称第 p 杯酒与第 q 杯酒是“ r 相似” 的。当然两杯“ r 相似”(r > 1)的酒同时也是“ 1 相似”、“ 2 相似”、……、“ (r − 1) 相似”的。特别地,对于任意的 1 ≤ p , q ≤ n , p ≠ q ,第 p 杯酒和第 q 杯酒都 是“ 0 相似”的。
在品尝环节上,品酒师 Freda 轻松地评定了每一杯酒的美味度,凭借其专业的水准和经验成功夺取了“首席品酒家”的称号,其中第 i 杯酒 (1 ≤ i ≤ n) 的 美味度为 ai 。现在 Rainbow 公布了挑战环节的问题:本次大会调制的鸡尾酒有一个特点,如果把第 p 杯酒与第 q 杯酒调兑在一起,将得到一杯美味度为 ap*aq 的 酒。现在请各位品酒师分别对于 r = 0,1,2, ⋯ , n − 1 ,统计出有多少种方法可以 选出 2 杯“ r 相似”的酒,并回答选择 2 杯“ r 相似”的酒调兑可以得到的美味度的最大值。
输入输出格式
输入格式:
第 1 行包含 1 个正整数 n ,表示鸡尾酒的杯数。
第 2 行包含一个长度为 n 的字符串 S,其中第 i 个字符表示第 i 杯酒的标签。
第 3 行包含 n 个整数,相邻整数之间用单个空格隔开,其中第 i 个整数表示第 i 杯酒的美味度 ai 。
输出格式:
包括 n 行。第 i 行输出 2 个整数,中间用单个空格隔开。第 1 个整 数表示选出两杯“ (i − 1) 相似”的酒的方案数,第 2 个整数表示选出两杯 “ (i − 1) 相似”的酒调兑可以得到的最大美味度。若不存在两杯“ (i − 1) 相似” 的酒,这两个数均为 0 。
输入输出样例
10 ponoiiipoi 2 1 4 7 4 8 3 6 4 7
45 56 10 56 3 32 0 0 0 0 0 0 0 0 0 0 0 0 0 0
12 abaabaabaaba 1 -2 3 -4 5 -6 7 -8 9 -10 11 -12
66 120 34 120 15 55 12 40 9 27 7 16 5 7 3 -4 2 -4 1 -4 0 0 0 0
说明
【样例说明 1】
用二元组 (p, q) 表示第 p 杯酒与第 q 杯酒。
0 相似:所有 45 对二元组都是 0 相似的,美味度最大的是 8 × 7 = 56 。
1 相似: (1,8) (2,4) (2,9) (4,9) (5,6) (5,7) (5,10) (6,7) (6,10) (7,10) ,最大的 8 × 7 = 56 。
2 相似: (1,8) (4,9) (5,6) ,最大的 4 × 8 = 32 。
没有 3,4,5, ⋯ ,9 相似的两杯酒,故均输出 0 。
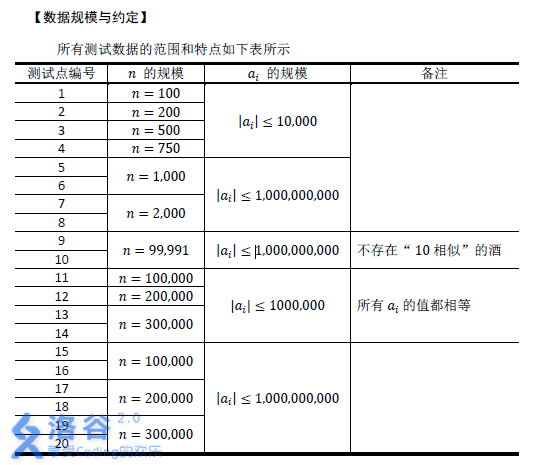
【时限1s,内存512M】
思路:
给定一个字符串,要求分别找出公共子串长度为0~n-1的串的数目。并且每个酒有一个值,求这些方案中哪两个值之积最大。
题意:
因为有负值,所以要同时维护最大值和最小值,负负得正。
一直70分,后来把best的初始化从-inf改成了LLONG_MIN就过了。
因为题目中r相似一定是r-1,r-2...相似的。所以处理一下严格r相似的,然后累加一下就好了。
题解好多都是用的并查集。单调栈其实也是一个道理。栈里存的就是这个区间。
碰到了height更小的时候就应该出栈了。每次就是把产生了贡献的区间并起来。
1 #include <iostream> 2 #include <set> 3 #include <cmath> 4 #include <stdio.h> 5 #include <cstring> 6 #include <algorithm> 7 #include <vector> 8 #include <queue> 9 #include <map> 10 #include <bits/stdc++.h> 11 using namespace std; 12 typedef long long LL; 13 #define inf 0x7f7f7f7f 14 15 const int maxn = 3e5 + 5; 16 17 char str[maxn]; 18 int n, s[maxn]; 19 LL val[maxn]; 20 int sa[maxn]; 21 int t1[maxn], t2[maxn], c[maxn]; 22 int rnk[maxn], height[maxn]; 23 LL cnt[maxn], best[maxn]; 24 int top, sta[maxn], mx[maxn], mi[maxn], sz[maxn]; 25 26 void build_sa(int s[], int n, int m) 27 { 28 int i, j, p, *x = t1, *y = t2; 29 for(i = 0; i < m; i++)c[i] = 0; 30 for(i = 0; i < n; i++)c[x[i] = s[i]]++; 31 for(i = 1; i < m; i++)c[i] += c[i - 1]; 32 for(i = n - 1; i >= 0; i--)sa[--c[x[i]]] = i; 33 for(j = 1; j <= n; j <<= 1){ 34 p = 0; 35 for(i = n - j; i < n; i++)y[p++] = i; 36 for(i = 0; i < n; i++)if(sa[i] >= j)y[p++] = sa[i] - j; 37 for(i = 0; i < m; i++)c[i] = 0; 38 for(i = 0; i < n; i++)c[x[y[i]]]++; 39 for(i = 1; i < m; i++)c[i] += c[i - 1]; 40 for(i = n - 1; i >= 0; i--)sa[--c[x[y[i]]]] = y[i]; 41 swap(x, y); 42 p = 1; 43 x[sa[0]] = 0; 44 for(i = 1; i < n; i++) 45 x[sa[i]] = y[sa[i - 1]] == y[sa[i]] && y[sa[i - 1] + j] == y[sa[i] + j] ? p - 1: p++; 46 if(p >= n)break; 47 m = p; 48 } 49 } 50 51 void get_height(int s[], int n) 52 { 53 int i, j, k = 0; 54 for(i = 0; i <= n; i++){ 55 rnk[sa[i]] = i; 56 } 57 for(i = 1; i <= n; i++){ 58 if(k)k--; 59 j = sa[rnk[i] - 1]; 60 while(s[i + k] == s[j + k])k++; 61 height[rnk[i]] = k; 62 } 63 } 64 65 void work() 66 { 67 int ksz, kmx, kmi; 68 for(int i = 2; i <= n; i++){ 69 ksz = 1; 70 kmx = kmi = val[sa[i - 1]]; 71 while(top && sta[top] >= height[i]){ 72 cnt[sta[top]] += 1LL * sz[top] * ksz; 73 best[sta[top]] = max(best[sta[top]], max(1LL * mx[top] * kmx, 1LL * mi[top] * kmi)); 74 ksz += sz[top]; 75 kmx = max(kmx, mx[top]); 76 kmi = min(kmi, mi[top]); 77 --top; 78 } 79 ++top; 80 sta[top] = height[i]; 81 sz[top] = ksz; 82 mi[top] = kmi; 83 mx[top] = kmx; 84 } 85 ksz = 1; 86 kmx = kmi = val[sa[n]]; 87 for(int i = top; i >= 1; i--){ 88 cnt[sta[i]] += 1LL * sz[i] * ksz; 89 best[sta[i]] = max(best[sta[i]], max(1LL * mx[i] * kmx, 1LL * mi[i] * kmi)); 90 ksz += sz[i]; 91 kmx = max(kmx, mx[i]); 92 kmi = min(kmi, mi[i]); 93 } 94 } 95 96 int main() 97 { 98 scanf("%d", &n); 99 scanf("%s", str + 1); 100 best[0] = LLONG_MIN; 101 //cout<<best[0]<<endl; 102 //cout<<-inf<<endl; 103 for(int i = 1; i <= n; i++){ 104 scanf("%lld", &val[i]); 105 s[i] = str[i]; 106 cnt[i] = 0; 107 best[i] = LLONG_MIN; 108 } 109 build_sa(s, n + 1, 300); 110 /*for(int i = 0; i <= n + 1; i++){ 111 cout<<sa[i]<<endl; 112 }*/ 113 get_height(s, n); 114 work(); 115 for(int i = n - 2; i >= 0; i--){ 116 cnt[i] += cnt[i + 1]; 117 best[i] = max(best[i], best[i + 1]); 118 } 119 for(int i = 0; i < n; i++){ 120 if(!cnt[i])best[i] = 0; 121 printf("%lld %lld ", cnt[i], best[i]); 122 } 123 124 125 return 0; 126 }