数论

1.gcd&exgcd

gcd 辗转相除法求最大公约数

辗转相除法：

设两数为a、b(a>b)，求a和b最大公约数(a，b)的步骤如下：用a除以b，得a÷b=q......r1(0≤r1)。若r1=0，则(a，b)=b；若r1≠0，则再用b除以r1，得b÷r1=q......r2 (0≤r2）.若r2=0，则(a，b)=r1，若r2≠0，则继续用r1除以r2，……如此下去，直到能整除为止。其最后一个余数为0的被除数的除数即为(a, b)的最大公约数。

例如：a=25,b=15，a/b=1......10,b/10=1......5,10/5=2.......0,最后一个余数为0的被除数的除数就是5, 5就是所求最大公约数。

性质：gcd(a,b)=gcd(b,a)=gcd(-a,b)=gcd(|a|,|b|)

int gcd(int a,int b)
{
	if(b==0)
	return a;
	else 
	return gcd(b,a%b);
}

exgcd

对于不完全为 0 的非负整数 a，b，gcd（a，b）表示 a，b 的最大公约数，必然

存在整数对 x，y ，使得 gcd（a，b）=ax+by

int gcd(int a,int b,int &x,int &y){
    if (b==0){
        x=1,y=0;
        return a;
    }
    int q=gcd(b,a%b,y,x);
    y-=a/b*x;
    return q;
}

2.素数

素数测试试除法

给定一个合数n（这里，n是待分解的整数），试除法看成是用小于等于n的每个素数去试除待分解的整数。如果找到一个数能够整除除尽，这个数就是待分解整数的因子。试除法一定能够找到n的因子。因为它检查n的所有可能的因子，所以如果这个算法“失败”，也就证明了n是个素数。

试除法可以从几条途径来完善。例如，n的末位数不是0或者5，那么算法中就可以跳过末位数是5的因子。如果末位数是2，检查偶数因子就可以了。

埃筛

首先，2是公认最小的质数，所以，先把所有2的倍数去掉；然后剩下的那些大于2的数里面，最小的是3，所以3也是质数；然后把所有3的倍数都去掉，剩下的那些大于3的数里面，最小的是5，所以5也是质数......
　　上述过程不断重复，就可以把某个范围内的合数全都除去（就像被筛子筛掉一样），剩下的就是质数了。

因为素数的分布，是有规律可循滴——这就是大名鼎鼎的素数定理。
　　稍微懂点数学的，应该知道素数的分布是越往后越稀疏。或者说，素数的密度是越来越低。而素数定理，说白了就是数学家找到了一些公式，用来估计某个范围内的素数，大概有几个。在这些公式中，最简洁的就是x/ln(x)，公式中的 ln 表示自然对数（估计很多同学已经忘了啥叫自然对数）。假设要估计1,000,000以内有多少质数，用该公式算出是72,382个，而实际有78,498个，误差约8个百分点。该公式的特点是：估算的范围越大，偏差率越小。
　　有了素数定理，就可以根据要打印的质数个数，反推出这些质数分布在多大的范围内。因为这个质数分布公式有一定的误差（通常小于15%）。为了保险起见，把反推出的素数分布范围再稍微扩大15%，应该就足够了。

存储方式：1.用int数组 但是比较浪费空间 2.用bool数组 全部初始化为true 3.按位存储

 

 

唯一因子分解定理

任何一个大于1的自然数

  

，都可以唯一分解成有限个质数的乘积

  

，这里

  

均为质数，其诸指数

  

是正整数。

 

 

3.模运算

定理：

模运算与基本四则运算有些相似，但是除法例外。其规则如下：

(a + b) % p = (a % p + b % p) % p （1）

(a - b) % p = (a % p - b % p) % p （2）

(a * b) % p = (a % p * b % p) % p （3）

(a^b) % p = ((a % p)^b) % p （4）

结合律：

((a+b) % p + c) % p = (a + (b+c) % p) % p （5）

((a*b) % p * c)% p = (a * b*c) % p （6）// (a%p*b)%p=(a*b)%p

交换律：

(a + b) % p = (b+a) % p （7）

(a * b) % p = (b * a) % p （8）

分配律：

((a +b)% p * c) % p = ((a * c) % p + (b * c) % p) % p （9）

重要定理：

若a≡b (% p)，则对于任意的c，都有(a + c) ≡ (b + c) (%p)；（10）

若a≡b (% p)，则对于任意的c，都有(a * c) ≡ (b * c) (%p)；（11）

若a≡b (% p)，c≡d (% p)，则 (a + c) ≡ (b + d) (%p)，(a - c) ≡ (b - d) (%p)，

(a * c) ≡ (b * d) (%p)； （12）

 

快速幂

以下以求a的b次方来介绍[1] 

把b转换成二进制数。

该二进制数第i位的权为

 

例如

11的二进制是1011

11 = 2³×1 + 2²×0 + 2¹×1 + 2º×1

因此，我们将a¹¹转化为算

 

用位运算实现：

b & 1//取b二进制的最低位，判断和1是否相同，相同返回1，否则返回0，可用于判断奇偶

b>>1//把b的二进制右移一位，即去掉其二进制位的最低位

递归版：
ll pow(ll a,ll i){
  if (i==0) return 1;
  int temp=pow(a,i>>1);
  temp=temp*temp%MOD;
  if (i&1) temp=(ll)temp*a%MOD;
  return temp%MOD;
}
非递归版：
ll f(ll a,ll b,ll n){
  int t,y;
  t=1; y=a;
  while (b!=0){
    if (b&1==1) t=t*y%n;
    y=y*y%n; b=b>>1;
  }
  return t;
}

矩阵快速幂 大白p199

 

 

4.miller_rabin素性测试 $O(lgn)

p为素数, 0<a<p  如果a^2 mod p = 1 则 a mod p =1或者 a mod p =-1即a mod p = p-1

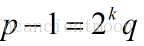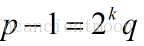任何一个素数p都能用表示

如果一个数不满足上诉条件，则这个数一定为合数；

如果一个数满足上诉条件，则它可能是素数，也可能是合数，但它是素数的概率（0.75）大于

它是合数的概率。为了降低误判（将合数判为合数），多次运行该算法，降低错误率

 

5.pollard_rho启发式分解 $O(v^{1/4}lgV)$

 

对于任意两个正整数x，y，有 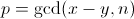 。如果结果p为1时，说明x-y与n是互素的，则需要继续寻找一个y；如果结果p不是1，则p为n的一个因子。

        每次可以调用 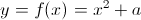 来确定一个新的y，其中a为任意数。

 

 

6.欧拉筛法$O(n)$