最近数据结构刚好看到了伸展树,在想这个东西有什么应用,于是顺便学习一下。
二叉查找树(BST),对于树上的任意一个节点,节点的左子树上的关键字都小于这个节点的关键字,节点的右子树上的关键字都大于这个节点的关键字。
对二叉查找树进行中序遍历,可以得到一个有序的序列。
下面这些操作的期望复杂度是$O(log N)$,但是如果BST中的数据是有序的序列BST就会变成一条链,复杂度会退化成$O(N)$
为了避免越界减少边界情况的特殊判断,一般在BST中额外插入一个关键码为正无穷和一个关键码为负无穷的节点。
1 struct BST { 2 int l, r; 3 int val; 4 }a[SIZE]; 5 int tot, root, INF = 1 << 30; 6 7 int NEW(int val) 8 { 9 a[++tot].val = val; 10 return tot; 11 } 12 13 void build() 14 { 15 NEW(-INF), NEW(INF); 16 root = 1; 17 a[1].r = 2; 18 }
检索时,如果当前节点p的关键字等于val,则已经找到。
如果p的关键字大于val,如果p的左子节点为空说明val不存在,否则在p的左子树中递归进行检索。
如果p的关键字小于val,如果p的右子节点为空说明val不存在,否则在p的右子树中递归进行检索。
1 int Get(int p, int val) 2 { 3 if(p == 0)return 0; 4 if(val == a[p].val)return p; 5 return val < a[p].val ? Get(a[p].l, val) : Get(a[p].r, val); 6 }
插入时,先执行检索操作,知道发现走向的p的子节点为空说明val不存在时,直接建立新节点。
1 void Insert(int &p, int val) 2 { 3 if(p == 0){ 4 p = New(val); 5 return; 6 } 7 if(val == a[p].val) return; 8 if(val < a[p].val) Insert(a[p].l, val); 9 else Insert(a[p].r, val); 10 }
val的后继指的是在BST中关键码大于val的前提下,关键码最小的节点。
求后继的过程:初始化ans为具有正无穷关键码的那个节点的编号,然后在BST中检索val。检索过程中,每经过一个点,看看能不能更新ans
当检索完成后,可能没有找到val,此时ans就是答案。
也有可能找到了关键字是val的节点p,但是p没有右子树,那么ans也就是答案。
也有可能是p有右子树,那么说明val的后继不是在刚刚已经经过的那些节点中,所以还要从p的右子节点出发,一直往左走。
1 nt GetNext(int val) 2 { 3 int ans = 2; 4 int p = root; 5 while(p){ 6 if(val == a[p].val){ 7 if(a[p].r > 0){ 8 p = a[p].r; 9 while(a[p].l > 0) p = a[p].l; 10 ans = p; 11 } 12 break; 13 } 14 if(a[p].val > val && a[p].val < a[ans].val)ans = p; 15 p = val < a[p].val ? a[p].l : a[p].r; 16 } 17 return ans; 18 }
删除节点时,也需要先检索val得到节点p。
如果p的孩子只有一个,那么可以直接删除,让p的子节点代替p。
如果p的孩子有两个,就需要在BST中找到val的后继节点nxt。
因为nxt没有左子树,所以可以直接让nxt的右子树代替nxt,然后让nxt代替p。
1 void remove(int val) 2 { 3 int &p = root; 4 while(p){ 5 if(val == a[p].val) break; 6 p = val < a[p].val ? a[p].l : a[p].r; 7 } 8 if(p == 0)return ; 9 if(a[p].l == 0){ 10 p = a[p].r; 11 } 12 else if(a[p].r == 0){ 13 p = a[p].l; 14 } 15 else{ 16 int nxt = a[p].r; 17 while(a[nxt].l > 0)nxt = a[nxt].l; 18 remove(a[nxt].val); 19 a[nxt].l = a[p].l, a[nxt].r = a[p].r; 20 p = nxt; 21 } 22 }
AVL树,是带有平衡条件的二叉查找树。
每个节点的左子树和右子树的高度最多差1。这样就可以使整棵树的深度维持在$O(log N)$
要维持平衡的条件,主要改变的是插入时的操作。
当我们插入了一个节之后,某一条路径上的节点有可能平衡条件被破坏,这时候我们就需要进行旋转操作使他们重新达到平衡条件。
插入时,沿着节点到根更新平衡信息,找到第一个平衡被破坏了的节点(最深的一个)a。
a的两棵子树的高度差2,如果是对a的左儿子的左子树或a的右儿子的右子树进行插入,那么只用进行一次单旋转。
比如这样: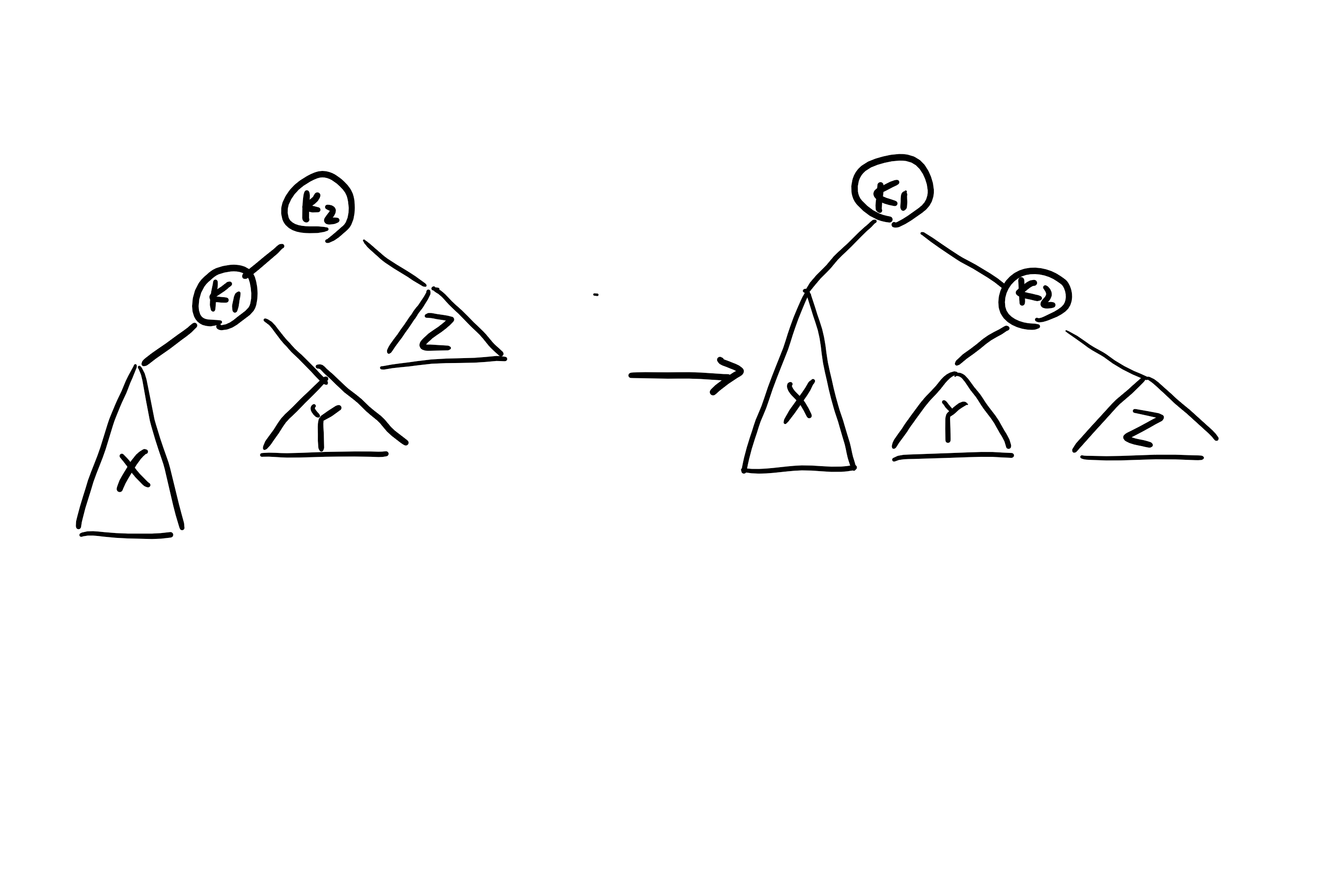

如果是对a的左儿子的右子树或是a的右儿子的左子树进行插入,需要进行一次双旋转。而实际上就是先将k1与k2进行一次旋转,再与k3旋转。
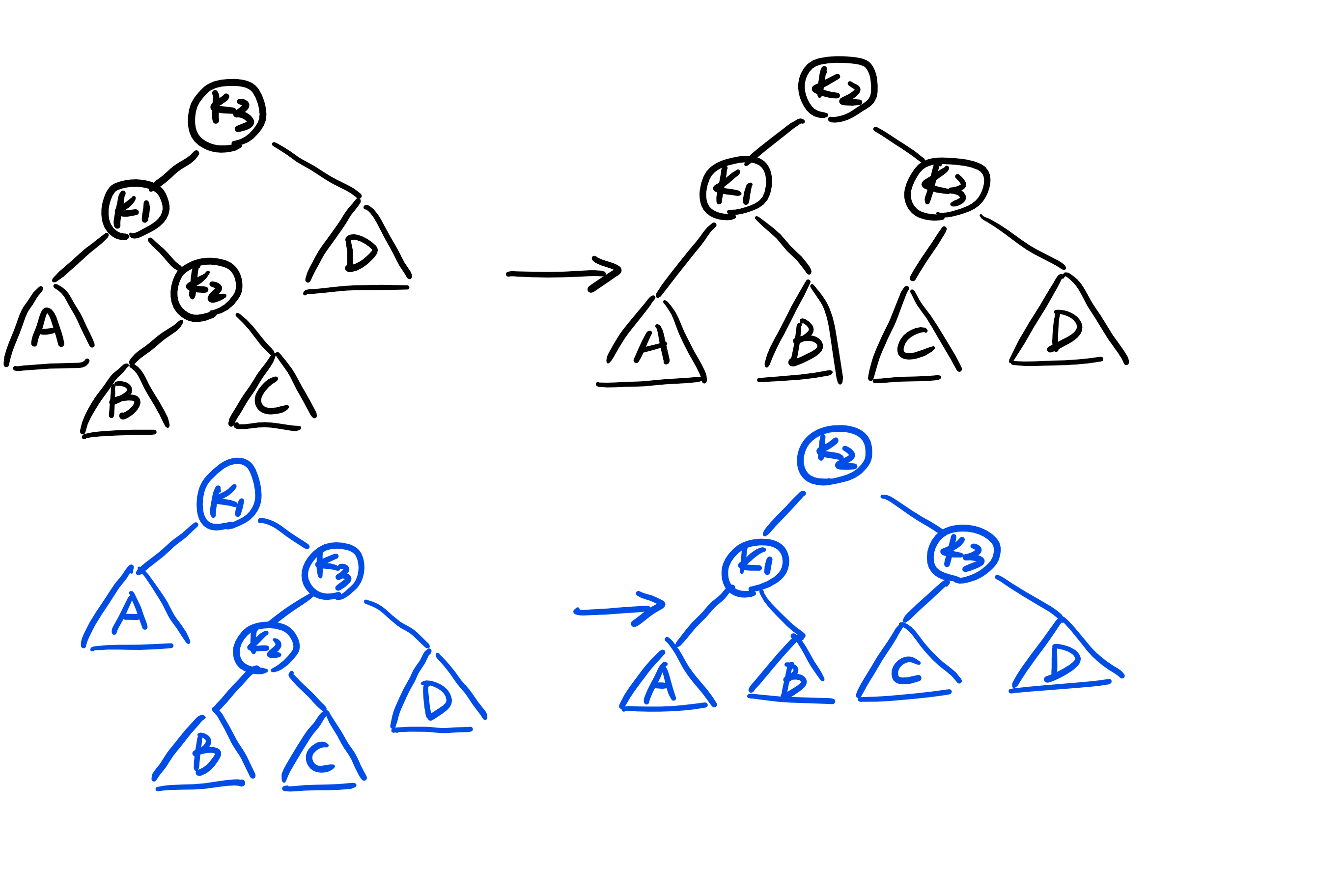
右旋就是把k1变成k2的父节点,k2作为k1的右子节点。zig(p)可以理解成把p的左子节点绕着p向右旋转。
1 void zig(int &p) 2 { 3 int q = a[p].l; 4 a[p].l = a[q].r, a[q].r = p; 5 p = q; 6 }
左旋zag(p)可以理解成把p的右子节点绕着p向左旋转。
1 void zag(int &p) 2 { 3 int q = a[p].r; 4 a[p].r = a[q].l, a[q].l = p; 5 p = q; 6 }
删除操作时,由于支持旋转,我们可以直接找到需要删除的节点,把他旋转成叶节点后直接删除。
伸展树(spaly tree),保证从空树开始任意连续M次对树的操作最多花费$O(M log N)$时间,但是并不排除任意一次操作花费$O(N)$时间的可能。
当一个节点被访问,就将他移动到根上。称为Splay操作。
Spaly操作:令X是在访问路径上的一个(非根)节点,如果X的父节点是树根,就只需要旋转X和树根。
否则分两种情况。

举个书上的习题作为例子。

在实际应用中,我们可以用伸展树维护一些区间的操作。
比如我们要提取区间[a,b],那么我们将a前面一个数对应的结点转到树根,将b 后面一个结点对应的结点转到树根的右边,那么根右边的左子树就对应了区间[a,b]。
与线段树相比,伸展树功能更强大,它能解决以下两个线段树不能解决的问题:
(1) 在a后面插入一些数。方法是:首先利用要插入的数构造一棵伸展树,接着,将a 转到根,并将a 后面一个数对应的结点转到根结点的右边,最后将这棵新的子树挂到根右子结点的左子结点上。
(2) 删除区间[a,b]内的数。首先提取[a,b]区间,直接删除即可。
关于伸展树的实现代码可以参考kuangbin博客中的转载
CH上有一道模板例题
http://contest-hunter.org:83/contest/0x40「数据结构进阶」例题/4601%20普通平衡树
要求实现一下六种操作:
1. 插入x数
2. 删除x数(若有多个相同的数,因只删除一个)
3. 查询x数的排名(若有多个相同的数,因输出最小的排名)
4. 查询排名为x的数
5. 求x的前驱(前驱定义为小于x,且最大的数)
6. 求x的后继(后继定义为大于x,且最小的数)
因为给的数可能会重复,而删除时只能删除一个,所以用cnt来记录这个值出现了的次数。
还要求查询排名,所以给节点增加一个size属性,记录以该节点为根的子树中所有节点的cnt之和。
在插入、删除和旋转时从下往上更新size信息。
1 //#include<bits/stdc++> 2 #include<stdio.h> 3 #include<iostream> 4 #include<algorithm> 5 #include<cstring> 6 #include<stdlib.h> 7 #include<queue> 8 #include<map> 9 #include<stack> 10 #include<set> 11 12 #define LL long long 13 #define ull unsigned long long 14 #define inf 0x3f3f3f3f 15 16 using namespace std; 17 18 const int SIZE = 1e5 + 10; 19 struct Treap{ 20 int l, r; 21 int val, dat; 22 int cnt, size; 23 }a[SIZE]; 24 int tot, root, n, INF = 0x7fffffff; 25 26 int New(int val) 27 { 28 a[++tot].val = val; 29 a[tot].dat = rand(); 30 a[tot].cnt = a[tot].size = 1; 31 return tot; 32 } 33 34 void Update(int p) 35 { 36 a[p].size = a[a[p].l].size + a[a[p].r].size + a[p].cnt; 37 } 38 39 void build() 40 { 41 New(-INF), New(INF); 42 root = 1, a[1].r = 2; 43 Update(root); 44 } 45 46 int GetRankByVal(int p, int val) 47 { 48 if(p == 0)return 0; 49 if(val == a[p].val) return a[a[p].l].size + 1; 50 if(val < a[p].val)return GetRankByVal(a[p].l, val); 51 return GetRankByVal(a[p].r, val) + a[a[p].l].size + a[p].cnt; 52 } 53 54 int GetValByRank(int p, int rank) 55 { 56 if(p == 0)return INF; 57 if(a[a[p].l].size >= rank)return GetValByRank(a[p].l, rank); 58 if(a[a[p].l].size + a[p].cnt >= rank)return a[p].val; 59 return GetValByRank(a[p].r, rank - a[a[p].l].size - a[p].cnt); 60 } 61 62 void zig(int &p) 63 { 64 int q = a[p].l; 65 a[p].l = a[q].r; 66 a[q].r = p; 67 p = q; 68 Update(a[p].r); 69 Update(p); 70 } 71 72 void zag(int &p) 73 { 74 int q = a[p].r; 75 a[p].r = a[q].l; 76 a[q].l = p; 77 p = q; 78 Update(a[p].l); 79 Update(p); 80 } 81 82 void Insert(int &p, int val) 83 { 84 if(p == 0){ 85 p = New(val); 86 return; 87 } 88 if(val == a[p].val){ 89 a[p].cnt++; 90 Update(p); 91 return; 92 } 93 if(val < a[p].val){ 94 Insert(a[p].l, val); 95 if(a[p].dat < a[a[p].l].dat)zig(p);//不满足堆性质,右旋 96 } 97 else{ 98 Insert(a[p].r, val); 99 if(a[p].dat < a[a[p].r].dat)zag(p);//不满足堆性质,左旋 100 } 101 Update(p); 102 } 103 104 int GetPre(int val) 105 { 106 int ans = 1; 107 int p = root; 108 while(p){ 109 if(val == a[p].val){ 110 if(a[p].l > 0){ 111 p = a[p].l; 112 while(a[p].r > 0)p = a[p].r; 113 ans = p; 114 } 115 break; 116 } 117 if(a[p].val < val && a[p].val > a[ans].val) ans = p; 118 p = val < a[p].val?a[p].l : a[p].r; 119 } 120 return a[ans].val; 121 } 122 123 int GetNext(int val) 124 { 125 int ans = 2; 126 int p = root; 127 while(p){ 128 if(val == a[p].val){ 129 if(a[p].r > 0){ 130 p = a[p].r; 131 while(a[p].l > 0)p = a[p].l; 132 ans = p; 133 } 134 break; 135 } 136 if(a[p].val > val && a[p].val < a[ans].val )ans = p; 137 p = val < a[p].val ? a[p].l : a[p].r; 138 } 139 return a[ans].val; 140 } 141 142 void Remove(int &p, int val) 143 { 144 if(p == 0)return; 145 if(val == a[p].val){ 146 if(a[p].cnt > 1){ 147 a[p].cnt--; 148 Update(p); 149 return; 150 } 151 if(a[p].l || a[p].r){ 152 if(a[p].r == 0 || a[a[p].l].dat > a[a[p].r].dat){ 153 zig(p); 154 Remove(a[p].r, val); 155 } 156 else { 157 zag(p); 158 Remove(a[p].l, val); 159 } 160 Update(p); 161 } 162 else p = 0; 163 return; 164 } 165 val < a[p].val ? Remove(a[p].l, val) : Remove(a[p].r, val); 166 Update(p); 167 } 168 169 int main() 170 { 171 build(); 172 cin>>n; 173 while(n--){ 174 int opt, x; 175 scanf("%d%d", &opt, &x); 176 switch(opt){ 177 case 1: 178 Insert(root, x); 179 break; 180 case 2: 181 Remove(root, x); 182 break; 183 case 3: 184 printf("%d ", GetRankByVal(root, x) - 1); 185 break; 186 case 4: 187 printf("%d ", GetValByRank(root, x + 1)); 188 break; 189 case 5: 190 printf("%d ", GetPre(x)); 191 break; 192 case 6: 193 printf("%d ", GetNext(x)); 194 break; 195 } 196 } 197 return 0; 198 }