• python拓展3 常用算法

    知识内容：

    1.递归复习

    2.算法基础概念

    3.查找与排序

    参考资料：

    http://python3-cookbook.readthedocs.io/zh_CN/latest/index.html

    http://www.cnblogs.com/alex3714/articles/5474411.html

    关于时间复杂度：http://www.cnblogs.com/alex3714/articles/5910253.html

    关于递归：http://www.cnblogs.com/alex3714/articles/8955091.html

    一、递归复习

    1.什么是递归：函数内部自己调用自己

    2.递归的特点

    • 必须有一个明确的结束条件
    • 每次进入更深一层递归时，问题规模相比上次递归都应有所减少
    • 递归效率不高，递归层次过多会导致栈溢出

    3.看函数说结果

     1 def func1(x):
 2     print(x)
 3     func1(x-1)
 4 func1(5)
 5 # 一直打印到限制次数(无出口)
 6 
 7 def func2(x):
 8     if x > 0:
 9         print(x)
10         func2(x+1)
11 func2(5)
12 # 一直打印到限制次数(无出口)
13 
14 def func3(x):
15     if x > 0:
16         print(x)
17         func3(x-1)
18 func3(5) 
19 # 从5打印到1
20 
21 def func4(x):
22     if x > 0:
23         func4(x-1)
24         print(x)
25 func4(5)
26 # 从1打印到5

    4.经典递归

    (1)汉诺塔问题

    解决思路：

    假设有n个盘子：

    • 1.把n-1个圆盘从A经过C移动到B
    • 2.把第n个圆盘从A移动到C
    • 3.把n-1个小圆盘从B经过A移动到C

    1：

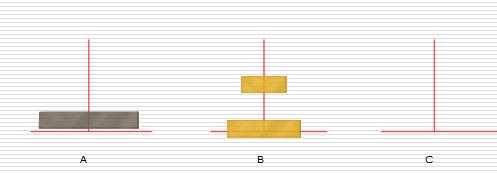
    2：

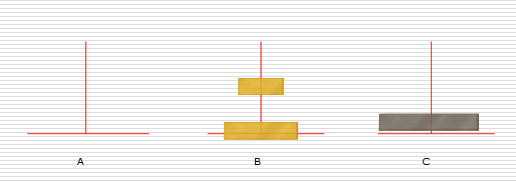
    3：

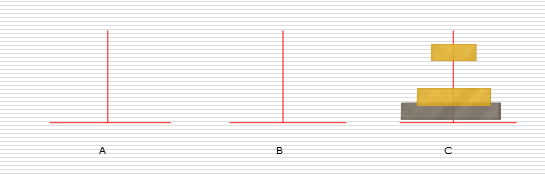
     代码：

     1 def hanoi(a, b, c, n):
 2     if n == 1:
 3         print(a, "->", c)       # 将n-1个盘子从a经过c移动到b
 4     else:
 5         hanoi(a, c, b, n-1)     # 将剩余的最后一个盘子从a移动到c
 6         print(a, "->", c)
 7         hanoi(b, a, c, n-1)     # 将n-1个盘子从b经过a移动到c
 8 
 9 
10 hanoi('柱子a', '柱子b', '柱子c', 4)

    总结：汉诺塔移动次数的递推式：h(x)=2h(x-1)+1

    (2)字符串逆序输出

    1 def rvs(s):
2     if s == "":
3         return s
4     else:
5         return rvs(s[1:]) + s[0]
6 
7 
8 s = rvs("Hello, Python")
9 print(s)

    5.尾递归

    定义：当递归调用是整个函数体中最后执行的语句且返回值不属于表达式的一部分时，这个递归调用就是尾递归。尾递归函数的特点是在回归过程中不用做任何操作，这个特性很重要，因为大多数现代的编译器会利用这种特点自动生成优化的代码。

    原理：当编译器检测到一个函数调用是尾递归的时候，它就覆盖当前的活动记录而不是在栈中去创建一个新的。编译器可以做到这点，因为递归调用是当前活跃期内最后一条待执行的语句，于是当这个调用返回时栈帧中并没有其他事情可做，因此也就没有保存栈帧的必要了。通过覆盖当前的栈帧而不是在其之上重新添加一个，这样所使用的栈空间就大大缩减了，这使得实际的运行效率会变得更高。

    尾递归实例：

    1 def calc(n):
2     print(n - 1)
3     if n > -50:
4         return calc(n-1)

    二、算法基础概念

    1.什么是算法

    算法就是一个计算过程，解决问题的方法

    算法（Algorithm）是指解题方案的准确而完整的描述，是一系列解决问题的清晰指令，算法代表着用系统的方法描述解决问题的策略机制。也就是说，能够对一定规范的输入，在有限时间内获得所要求的输出。如果一个算法有缺陷，或不适合于某个问题，执行这个算法将不会解决这个问题。不同的算法可能用不同的时间、空间或效率来完成同样的任务。一个算法的优劣可以用空间复杂度与时间复杂度来衡量

    一个算法应该具有以下七个重要的特征：

    • 有穷性（Finiteness）：算法的有穷性是指算法必须能在执行有限个步骤之后终止
    • 确切性(Definiteness)：算法的每一步骤必须有确切的定义
    • 输入项(Input)：一个算法有0个或多个输入，以刻画运算对象的初始情况，所谓0个输     入是指算法本身定出了初始条件
    • 输出项(Output)：一个算法有一个或多个输出，以反映对输入数据加工后的结果。没       有输出的算法是毫无意义的
    • 可行性(Effectiveness)：算法中执行的任何计算步骤都是可以被分解为基本的可执行       的操作步，即每个计算步都可以在有限时间内完成（也称之为有效性）
    • 高效性(High efficiency)：执行速度快，占用资源少
    • 健壮性(Robustness)：对数据响应正确

    2.时间复杂度及空间复杂度

    (1)时间复杂度

     1 print("hello, world")
 2 
 3 for i in range(n):
 4     print("hello, world")
 5 
 6 for i in range(n):
 7     for j in range(n):
 8         print("hello, world")
 9 
10 for i in range(n):
11     for j in range(n):
12         for k in range(n):
13             print("hello, world")

    问以上代码的运行时间谁最短？用什么方法来提现代码(算法)的运行快慢呢？答案就是用时间复杂度来衡量

    常见算法的时间复杂度(由小到大排列)：O(1)  O(logn)  O(n)  O(nlogn)  O(n^2) O(n^2logn)  O(n^3)

    实例：

     1 print('hello world')
 2 print('hello python')   # O(1)    大O，可以认为它的含义是“order of”(大约是)
 3 
 4 n= 64
 5 while n>1:
 6     print(n)     # O(logn)　　# n=64是输出依次为: 64 32 16 8 4 2 
 7     n = n//2
 8 
 9 for i in range(n):
10     print(i)      # O(n)
11 
12 for i in range(n):
13     for j in range(n):
14         print('hello world')   # O(n^2)
15 
16 for i in range(n):
17     for j in range(n):
18         for k in range(n):
19             print('hello world')   # O(n^3)

    注：切片的复杂度是O(n) ，因为切的时候是赋值

    总结：

    • 时间复杂度是用来估计算法运行时间的一个式子(单位)
    • 一般来说，时间复杂度高的算法比算法时间复杂度低的算法慢
    • 循环减半的过程就是O(logn)，几次循环就是n的几次方的复杂度

    (2)空间复杂度

    空间复杂度是用来评估算法内存占用大小的一个式子，常见的空间复杂度：O(1)  O(n)  O(n^2)

    空间换时间：计算机的资源很充足，可以用空间的消耗来换取一定的时间

    三、查找与排序

    1.常用查找

    (1)列表查找

    列表查找：从列表中查找指定元素

    输入：列表、待查找的元素，输出：元素下标或未查找到元素

    列表查找的方法：顺序查找和二分查找

    • 顺序查找：从列表第一个元素开始，顺序进行搜索直到找到为止
    • 二分查找：从有序列表的后续区开始查找，通过对查找的值和候选区中间的值进行比较，使候选区减半(二分查找的列表必须有序!)

    以上两种查找的代码如下：

    # 顺序查找 时间复杂 O(n)
def linear_search(find, data_list):
    for i in range(len(data_list)):
        if data_list[i] == find:
            return i
    return -1


# 二分查找 时间复杂 O(logn)
def binary_search(find, data_list):
    low = 0
    high = len(data_list)
    while low <= high:
        mid = (low + high) // 2
        # 找到find
        if data_list[mid] == find:
            return mid
        # find在左半边
        elif data_list[mid] > find:
            high = mid - 1
        # find在右半边
        else:
            low = mid + 1
    # 未找到find返回-1
    return -1

    (2)查找练习

    现在有一个学员信息列表(按id增序排列)，格式为：

    1 [
2     {"id": 1001, "name": "张三", "age": 20},
3     {"id": 1002, "name": "woz", "age": 22},
4     {"id": 1003, "name": "alex", "age": 23},
5     {"id": 1004, "name": "hf", "age": 26},
6     {"id": 1005, "name": "kk", "age": 27},
7 ]

    现在要求修改二分查找代码，输入学生id，输出该学生在该列表下的下标并输出完整的学生信息

    实现代码如下：

     1 import random
 2 stu_info = []       # 存储学生信息的列表
 3 
 4 # 随机生成n个数据
 5 def random_list(n):
 6     ids = list(range(1001, 1001+n))
 7     n1 = ["王", "赵", "李", "孙", "钱", "曾"]
 8     n2 = ["浩", "杰", "丽",  "", ""]
 9     n3 = ['强', '国', "兰"]
10     for i in range(n):
11         stu_age = random.randint(20, 30)
12         stu_id = ids[i]
13         stu_name = random.choice(n1)+random.choice(n2)+random.choice(n3)
14         stu_info.append({"id": stu_id, "age": stu_age, "name":stu_name})
15 
16 # 二分查找
17 def bin_search(data_set, find):
18     low = 0
19     high = len(data_set) - 1
20     while low <= high:
21         mid = (low+high)//2
22         if data_set[mid]["id"] == find:
23             return mid
24         elif data_set[mid]["id"] < find:
25             low = mid + 1
26         else:
27             high = mid - 1
28     return -1
29 
30 # 搜索信息
31 def search_info(info, find):
32     res = bin_search(info, find)
33     if res == -1:
34         print("没有找到")
35     else:
36         print(info[res])
37 
38 
39 random_list(15)
40 print("以下是所有学生的id信息: ")
41 # print(stu_info)
42 for item in stu_info:
43     print(item["id"], end=" ")
44 sid = int(input("
请输入你想要查找的学生的id: ").strip())
45 search_info(stu_info, sid)

    2.常用排序

    常用的排序有以下几种：

    (1)排序：将无序序列变为有序序列

    输入：无序序列，输出：有序序列

     

    (2)应用场景

    • 各种榜单
    • 各种表格
    • 给二分查找用
    • 给其他算法用

    (3)冒泡排序、选择排序、插入排序(必须背下来)

    算法关键点：无序区和有序区

    冒泡排序

    思路：首先，列表每两个相邻的数比较大小，如果前边的比后边的大那么这两个数就互换位置，另外冒泡排序的排序趟数为n-1

     1 # 冒泡排序:
 2 import random
 3 
 4 def bubble_sort(s):
 5     for i in range(len(s)-1):
 6         for j in range(len(s)-i-1):
 7             if s[j] > s[j+1]:
 8                 s[j], s[j+1] = s[j+1], s[j]
 9 
10 data = list(range(100))
11 random.shuffle(data)            # 打乱列表中的数
12 print(data)
13 bubble_sort(data)               # 冒泡排序
14 print(data) 
     1 # 冒泡排序优化:   如果冒泡排序中执行一趟而没有发生交互，则列表已经是有序状态，可以直接结束算法
 2 import random
 3 
 4 def bubble_sort(s):
 5     for i in range(len(s)-1):
 6         exchange = False
 7         for j in range(len(s)-i-1):
 8             if s[j] > s[j+1]:
 9                 s[j], s[j+1] = s[j+1], s[j]
10                 exchange = True
11         if not exchange:
12             break
13 
14 data = list(range(100))
15 random.shuffle(data)            # 打乱列表中的数
16 print(data)
17 bubble_sort(data)               # 冒泡排序
18 print(data)

    选择排序

    思路： 一趟遍历完记录最小的数，放到第一个位置；在一趟遍历记录剩余列表中的最小的数，继续放置，那么怎么选最小的数？

    每次假设最开始的为最小的数，然后从左至右扫描序列，记下最小值的位置。另外选择排序和冒泡排序一样也是n-1趟

     1 # 选择排序:
 2 import random
 3 
 4 def select_sort(s):
 5     for i in range(len(s)-1):
 6         min_locate = i                    # 每次的开始以第一个为最小值
 7         for j in range(i+1, len(s)):
 8             if s[j] < s[min_locate]:      # 两数比较，如果另外一个数比最小值小，说明这个数为最小值
 9                 min_locate = j              
10         s[i], s[min_locate] = s[min_locate], s[i]
11 
12 data = list(range(100))
13 random.shuffle(data)            # 打乱列表中的数
14 print(data)
15 select_sort(data)               # 选择排序
16 print(data)

    插入排序

    思路：元素被分为有序区和无序区两部分。最初有序区只有一个元素。每次从无序区中选择一个元素，插入到有序区的位置，直到无序区变空

     1 # 插入排序：
 2 import random
 3 
 4 def insert_sort(s):
 5     for i in range(1, len(s)):  # i 表示无序区的第一个数
 6         tmp = s[i]              # 要插入有序区的数
 7         j = i - 1               # 指向有序区最后一个位置
 8         while s[j] > tmp and j >= 0:
 9             # 循环终止条件 li[j]<=tmp or j==-1
10             s[j + 1] = s[j]     # 向后移动
11             j -= 1
12         s[j + 1] = tmp
13 
14 data = list(range(100))
15 random.shuffle(data)            # 打乱列表中的数据
16 print(data)
17 insert_sort(data)               # 插入排序
18 print(data)

    注：冒泡排序、选择排序、插入排序的时间复杂度均为O(n^2)

    (4)快速排序、堆排序、归并排序(排序NB三人组)

    快速排序

     1 # encoding: utf-8
 2 # __author__ = "wyb"
 3 # date: 2018/9/26
 4 
 5 
 6 def quick_sort(data, left, right):
 7     if left < right:
 8         mid = partition(data, left, right)
 9         quick_sort(data, left, mid-1)
10         quick_sort(data, mid+1, right)
11 
12 
13 def partition(data, left, right):
14     tmp = data[left]
15     while left < right:
16         while left < right and data[right] >= tmp:
17             right -= 1
18         data[left] = data[right]
19         while left < right and data[left] <= tmp:
20             left += 1
21         data[right] = data[left]
22     data[left] = tmp
23     return left
24 
25 
26 data = list(range(10))
27 quick_sort(data, 0, len(data)-1)
28 print(data)

    注：快速排序一般时间复杂度为O(nlogn)，最好复杂度为O(nlogn)，最坏复杂度为O(n*n)

    堆排序

     1 关于堆排序:
 2 堆排序实质上是利用了二叉树 
 3 实质上在工程中二叉树利用数组结构存储，抽象存储原理如下:
 4 二叉树可以转换成数组: 节点i的左右孩子分别是2*i+1和2*i+2 节点i的父节点是(i-1)/2
 5         
 6 大根堆和小根堆:
 7     大根堆: 树的任何一个子树的最大值是这颗子树的顶部
 8     小根堆: 树的任何一个子树的最小值是这颗子树的顶部
 9     
10 堆排序过程:
11     堆排序实际上就是利用堆结构的排序
12     建立一个大根堆(复杂度为O(n)) -> 使用heapInsert插入数 
13     然后把大根堆第一个数和最后一个数替换 拿出这个元素把堆的size-1 然后使用heapify对堆进行调整
14         
15 去掉堆顶的最大数或最小数: 
16     把堆顶(第一个元素)和最后一个元素交换，拿出这个元素然后把堆的size-1，然后对堆顶进行hapify调整
17     
18 优先级队列结构其实就是堆结构
     1 def sift(data, low, high):
 2     i = low
 3     j = 2 * i + 1
 4     tmp = data[i]
 5     while j <= high:    # 没到子树的最下边
 6         if j + 1 <= high and data[j] < data[j+1]:   # 如果有右孩子且比左孩子大
 7             j += 1  # j指向右孩子
 8         if data[j] > tmp:   # 孩子比最高领导大
 9             data[i] = data[j]   # 孩子填到父亲的空位上
10             i = j               # 孩子成为新父亲
11             j = 2 * i +1        # 新孩子
12         else:
13             break
14     data[i] = tmp           # 最高领导放到父亲位置
15 
16 def heap_sort(data):
17     n = len(data)
18     for i in range(n // 2 - 1, -1, -1):
19         sift(data, i, n - 1)
20     #堆建好了
21     for i in range(n-1, -1, -1):            # i指向堆的最后
22         data[0], data[i] = data[i], data[0] # 领导退休，刁民上位
23         sift(data, 0, i - 1)                # 调整出新领导

    归并排序

     1 def merge(a, b):
 2     c = []
 3     h = j = 0
 4     while j < len(a) and h < len(b):
 5         if a[j] < b[h]:
 6             c.append(a[j])
 7             j += 1
 8         else:
 9             c.append(b[h])
10             h += 1
11 
12     if j == len(a):
13         for i in b[h:]:
14             c.append(i)
15     else:
16         for i in a[j:]:
17             c.append(i)
18 
19     return c
20 
21 
22 def merge_sort(lists):
23     if len(lists) <= 1:
24         return lists
25     middle = len(lists)/2
26     left = merge_sort(lists[:middle])
27     right = merge_sort(lists[middle:])
28     return merge(left, right)

    (5)没什么人用的排序(基数排序、希尔排序、桶排序)

    这三种都是比较少用到的算法(了解即可)

    • 桶排序: 时间复杂度O(N) 额外空间复杂度O(N)
    • 计数排序: 时间复杂度O(N) 额外空间复杂度O(N)
    • 基数排序: 时间复杂度O(N) 额外空间复杂度O(N)
    • 上述三种都是非基于比较的排序，与被排序的样本数据实际情况很有关系，在实际中并不常用
    • 另外以上三种都是稳定的排序
    1 桶: 相当于一个容器，可以是数组中的某个位置也可以是双向链表也可以是一个队列也可以是一个堆
2 把相应东西放入相应桶内 然后再从低位置的桶依次到高位置 依次把东西倒出来
3     
4 eg: 数组arr长度为60 数据值为0到60 使用桶排序： 生成一个数组temp长度为61 依次遍历arr得到arr[i]
5     将temp对应的数组值++ temp[arr[i]] = temp[arr[i]] + 1 遍历完了之后遍历数组temp输出结果
6     每个下标对应几个值就把下标值输出几遍
7     实际上这个实例是计数排序 实质上是桶排序的一种实现
8     
9 基数排序将计数排序进行了改进，用10个桶进行排序 分别针对个位、十位、百位

    (6)排序算法的稳定性

    追求算法稳定性的意义: 第一次排序和第二次排序在某些值相等的情况下保持原来的排序顺序

    • 冒泡排序: 可以实现稳定(相等的情况下后一个继续往后走)
    • 插入排序: 可以实现稳定(相等就不往前插入)
    • 选择排序: 做不到稳定
    • 归并排序: 可以实现稳定(merge相等的时候就先移动左边的)
    • 快速排序: 做不到稳定(partition时做不到)
    • 堆排序: 做不到稳定
  • 相关阅读:
    CoreData数据库浅析
    FMDB第三方框架
    SQLite浅析
    iOS开发工程师面试题（二）
    iOS开发工程师面试题（一）
    RunTime&RunLoop初见
    GCD定时器
    2016年4月21百度iOS实习生在线笔试题&编程题
    网络天荒地老之UIWebView&WebKit
    expdp/impdp
  • 原文地址：https://www.cnblogs.com/wyb666/p/8990024.html
Copyright © 2020-2023  润新知