内容:
1、问题引入
2、暴力求解方法
3、优化方法
4、KMP算法
1、问题引入
原始问题:
对于一个字符串 str (长度为N)和另一个字符串 match (长度为M),如果 match 是 str 的子串,
请返回其在 str 第一次出现时的首字母下标,若 match 不是 str 的子串则返回 -1
注:子序列和子串的区别:子序列可以不连续,子串必须连续
2、暴力求解方法
暴力求解方法:将 str 从头开始遍历并与 match 逐次比较,若碰到了不匹配字母则终止此次遍历转而从 str 的 第二个字符开始遍历
并与 match 逐次比较,直到某一次的遍历每个字符都与 match 匹配否则返回 -1 。易知此种 做法的时间复杂度为 O(N*M)
注:KMP算法则给出求解该问题时间复杂度控制在 O(N) 的解法
3、优化方法
优化方法:借助next数组进行优化
在一个字符串中,每个字符之前的最长前缀和最长后缀的最大匹配长度就是next数组中的值,next数组在KMP算法中的目的就是决定下次匹配对象
注:前缀不能包含最后一个字符,后缀也不能包含第一个字符(前缀和后缀不能是字符串整体!)
next数组示例:
- 字符串为abcabcd,此时d位置上的next数组值就是3
- 字符串为aaaaab,此时b位置上的next数组值就是4
- 字符串为ababac,此时next数组值依次是-1、0、0、1、2、3
如何求next数组:
当串 match 长度 mlen=1 时,规定 next[0]=-1 。当 mlen=2 时,去掉 match[1] 之后只剩下 match[0] ,
大匹配子串长度为0(因为前缀子串不能包含串尾字符,后缀子串不能包含串首字符),即 next[1]=0
而当 mlen>2 时, next[n] (n>=2)都可以推算出来:
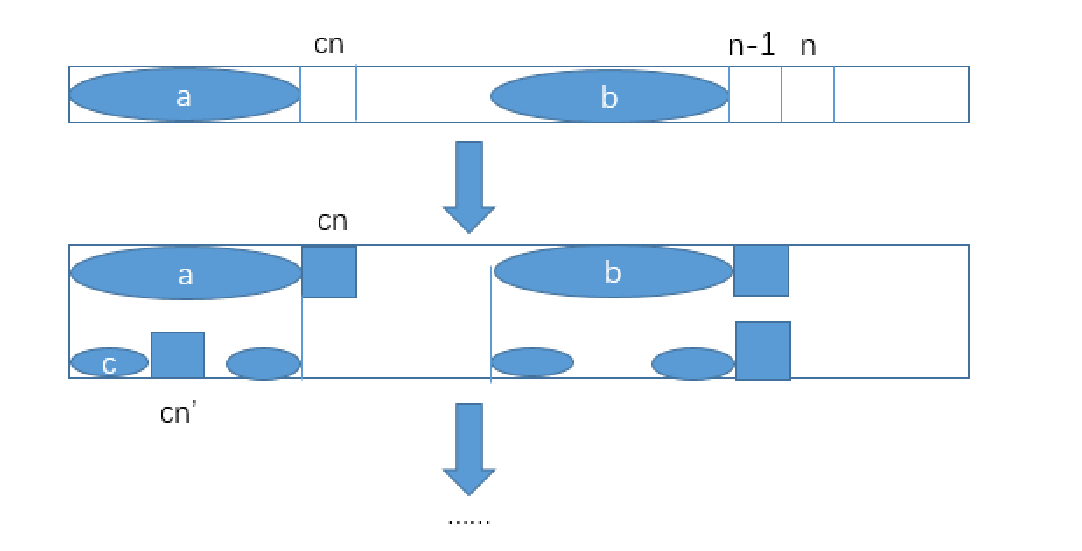
如上图所示,如果我们知道了next[n-1] ,那么 next[n] 的求解有两种情况:如果 match[cn]=match[n-1] ,
那么由a区域与b区域(a、b为最大匹配前缀子串和后缀字串)相同可知 next[n]=next[n1]+1 ;
如果 match[cn]!=match[n-1] ,那么求a区域中下一个能和b区域后缀子串中匹配的较大的一个,
即a区域 的大匹配前缀字串 c区域 ,将 match[n-1] 和c区域的后一个位置( cn' )上的字符比较,
如果相等则 next[n] 等于c区域的长度+1,而c区域的长度就是 next[cn] ( next数组的定义如此);
如果不等则将 cn 打 到 cn' 的位置继续和 match[n-1] 比较,直到 cn 被打到 0 为止(即next[cn]=-1 为止),那么此时next[n]=0
求next数组代码:
1 public static int[] getNextArray(char[] str) { 2 if (str.length == 1) { 3 return new int[] { -1 }; 4 } 5 int[] next = new int[str.length]; 6 next[0] = -1; 7 next[1] = 0; 8 int i = 2; 9 int cn = 0; 10 while (i < next.length) { 11 if (str[i - 1] == str[cn]) { 12 next[i++] = ++cn; 13 } else if (cn > 0) { 14 cn = next[cn]; 15 } else { 16 next[i++] = 0; 17 } 18 } 19 return next; 20 }
4、KMP算法
KMP算法的原理如下:
子串 match 的 next数组找到之后就可以进行 KMP 算法求解此问题了。 KMP 算法的逻辑是对于 str 的 i~(i+k) 部分 ( i 、 i+k 合法)
和 match 的 0~k 部分( k合法),如果有 str[i]=match[0] 、 str[i+1]=match[1] …… str[i+k-1]=match[k-1] ,但 str[i+k]!=[k] ,
那么 str 的 下标不用从i+k 变为 i+1 重新比较,只需将子串 str[0]~str[i+k-1] 的大匹配前缀子串的后一个字符 cn 重新与 str[i+k] 向后依次比较,
后面如果又遇到了不匹配的字符重复此操作即可:
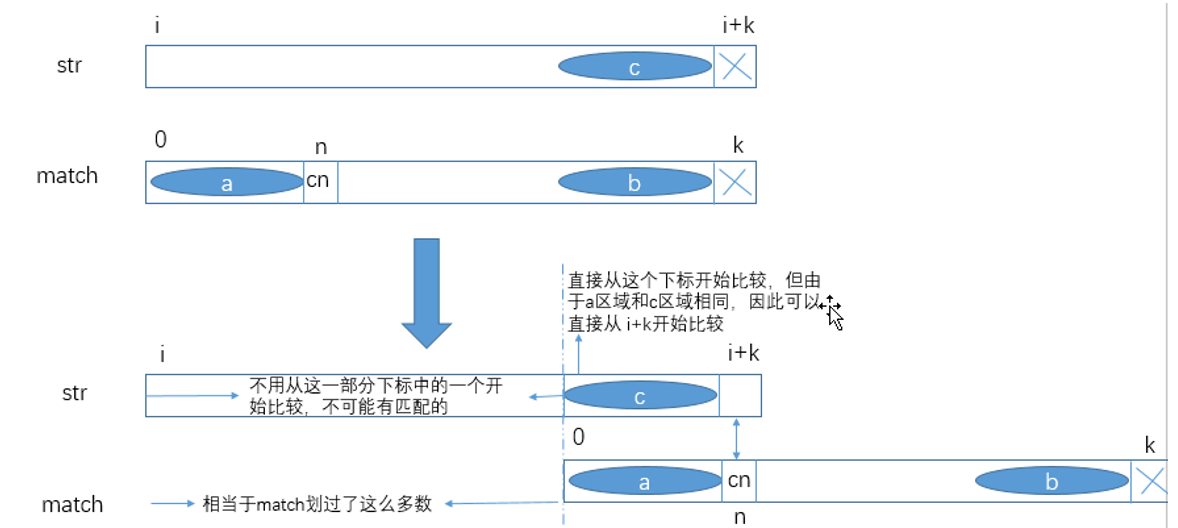
当遇到不匹配字符时,常规的做法是将 str 的遍历下标 sIndex 移到 i+1 的位置并将 match 的遍历下标 mIndex 移到 0 再依次比较,
这种做法并没有利用上一轮的比较信息(对下一轮的比较没有任何优化);
而 KMP 算法则不是这样,当遇到不匹配的字符str[i+k] 和 match[k] 时, str 的遍历指针 sIndex=i+k 不用动,
将 match 右滑并将其遍历指针 mIndex 打到子串 match[0]~match[k-1]的最大匹配前缀子串的后一个下标 n 的位 置。
然后 sIndex 从 i+k 开始, mIndex 从 n 开始,依次向后比较,若再遇到不匹配的数则重复此过程
KMP算法核心代码:
1 public static int getIndexOf(String s, String m) { 2 if (s == null || m == null || m.length() < 1 || s.length() < m.length()) { 3 return -1; 4 } 5 char[] str1 = s.toCharArray(); 6 char[] str2 = m.toCharArray(); 7 int i1 = 0; 8 int i2 = 0; 9 int[] next = getNextArray(str2); 10 while (i1 < str1.length && i2 < str2.length) { 11 if (str1[i1] == str2[i2]) { 12 i1++; 13 i2++; 14 } else if (next[i2] == -1) { 15 i1++; 16 } else { 17 i2 = next[i2]; 18 } 19 } 20 return i2 == str2.length ? i1 - i2 : -1; 21 }
可以发现 KMP 算法中 str 的遍历指针并没有回溯这个动作(只向后移动),当完成匹配时 sIndex 的移动次数小 于 N ,
否则 sIndex 移动到串尾也会终止循环,所以 while 对应的匹配过程的时间复杂度为 O(N) ( if(next[j] != -1){ j = next[j] } 的
执行次数只会是常数次,因此可以忽略)
完整的KMP代码及测试样例如下:
1 // KMP算法 2 public class KMP { 3 public static int getIndexOf(String s, String m) { 4 if (s == null || m == null || m.length() < 1 || s.length() < m.length()) { 5 return -1; 6 } 7 char[] str1 = s.toCharArray(); 8 char[] str2 = m.toCharArray(); 9 int i1 = 0; 10 int i2 = 0; 11 int[] next = getNextArray(str2); 12 while (i1 < str1.length && i2 < str2.length) { 13 if (str1[i1] == str2[i2]) { 14 i1++; 15 i2++; 16 } else if (next[i2] == -1) { 17 i1++; 18 } else { 19 i2 = next[i2]; 20 } 21 } 22 return i2 == str2.length ? i1 - i2 : -1; 23 } 24 25 public static int[] getNextArray(char[] str) { 26 if (str.length == 1) { 27 return new int[] { -1 }; 28 } 29 int[] next = new int[str.length]; 30 next[0] = -1; 31 next[1] = 0; 32 int i = 2; 33 int cn = 0; 34 while (i < next.length) { 35 if (str[i - 1] == str[cn]) { 36 next[i++] = ++cn; 37 } else if (cn > 0) { 38 cn = next[cn]; 39 } else { 40 next[i++] = 0; 41 } 42 } 43 return next; 44 } 45 46 public static void main(String[] args) { 47 System.out.println(getIndexOf("abcabcababaccc", "ababa")); 48 System.out.println(getIndexOf("just a test", "test")); 49 System.out.println(getIndexOf("justatest", "test")); 50 System.out.println(getIndexOf("asfawfasdf", "666")); 51 System.out.println(getIndexOf("absafasdcc", "ababa")); 52 } 53 }