内容:
1、递归与多态规划的关系
2、暴力递归
3、动态规划
1、递归与多态规划的关系
暴力递归:
- 把问题转化为规模缩小了的同类问题的子问题
- 有明确的不需要继续进行递归的条件(base case)
- 有当得到了子问题的结果之后的决策过程
- 不记录每一个子问题的解
动态规划:
- 从暴力递归中来
- 将每一个子问题的解记录下来,避免重复计算
- 把暴力递归的过程,抽象成了状态表达
- 并且存在化简状态表达,使其更加简洁的可能
P和NP:
P指的是我明确地知道怎么算,计算的流程很清楚;而NP问题指的是我不知道怎么算,但我知道怎么尝试(暴力递归)
2、暴力递归
n!问题:
1 // 求n! 2 public class Factorial { 3 // 普通方法 4 // 知道 n! 的定义,可以根据定义直接求解 5 public static long getFactorialByCommon(int n) { 6 long res = 1L; 7 for (int i = 1; i <= n; i++) { 8 res *= i; 9 } 10 return res; 11 } 12 13 // 递归方法 14 // 如果知道 (n-1)! 那通过 (n-1)! * n 不就得出 n! 于是可以这样尝试: 15 public static long getFactorialByRecursion(int n) { 16 if (n == 1) { 17 return 1L; 18 } 19 return (long) n * getFactorialByRecursion(n - 1); 20 } 21 22 public static void main(String[] args) { 23 int n = 5; 24 System.out.println(getFactorialByCommon(n)); 25 System.out.println(getFactorialByRecursion(n)); 26 } 27 }
汉诺塔问题:
问题描述:
汉诺塔问题是一个经典的问题。汉诺塔源于印度一个古老传说。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。
并且规定,任何时候,在小圆盘上都不能放大圆盘,且在三根柱子之间一次只能移动一个圆盘。问应该如何操作?
思路:该问题基础的一个模型就是,一个竿上放了2个圆盘,需要先将上面的那个移到辅助竿上,然后将底下的圆盘移到目标竹竿,后把辅助竿上的圆盘移回目标竹竿(递归过程)
代码:
1 // 汉诺塔问题 2 public class Hanoi { 3 4 public static void process(int N, String from, String to, String help){ 5 if(N==1){ 6 System.out.println("Move 1 from " + from + " to " + to); 7 } else{ 8 // 尝试把前n-1个圆盘暂时放到辅助竿上 -> 子问题 9 process(N-1, from, help, to); 10 // 将底下大的圆盘移到目标竿 11 System.out.println("Move " + N + " from " + from + " to " + to); 12 // 再尝试将辅助竿上的圆盘移回到目标竿 -> 子问题 13 process(N-1, help, to, from); 14 } 15 } 16 17 public static void main(String[] args) { 18 process(3, "左", "右", "中"); 19 } 20 }
打印字符串系列问题:
问题描述:
- 打印字符串的所有子序列
- 打印一个字符串的全部排列
- 打印一个字符串的全部排列,要求不要出现重复的排列
注意:字符串的子序列和子串有着不同的定义。子串指串中相邻的任意个字符组成的串,而子序列可以是串中任意个不同字符组成的串
尝试:开始时,令子序列为空串,扔给递归方法。首先来到字符串的第一个字符上,这时会有两个决策:
将这个字 符加到子序列和不加到子序列。这两个决策会产生两个不同的子序列,将这两个子序列作为这一级收集的信息扔给 子过程,子过程来到字符串的第二个字符上,对上级传来的子序列又有两个决策,……这样终能将所有子序列组 合穷举出来:

打印一个字符串的全排列过程:
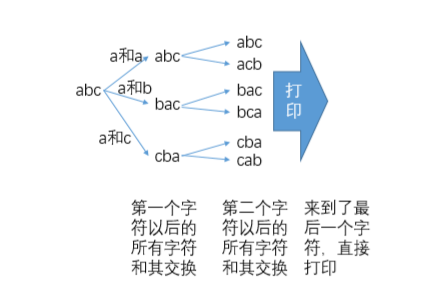
代码:
1 public class printString { 2 // swap two elements of a array of char 3 private static void swap(char[] chs, int i, int j){ 4 char temp = chs[i]; 5 chs[i] = chs[j]; 6 chs[j] = temp; 7 } 8 9 // 打印字符串的所有子序列 10 public static void printAllSubsquence(char[] strs, int i, String res){ 11 if(i==strs.length){ 12 System.out.println(res); 13 return; 14 } 15 printAllSubsquence(strs, i+1, res); 16 printAllSubsquence(strs, i+1, res+String.valueOf(strs[i])); 17 18 } 19 20 // 打印一个字符串的全部排列 21 public static void printAllPermutations(char[] strs, int i){ 22 if(i==strs.length){ 23 for(int t=0; t<strs.length; t++){ 24 System.out.print(strs[t]); 25 } 26 System.out.println(); 27 return; 28 } 29 for(int j=i; j<strs.length; j++){ 30 swap(strs, i, j); 31 printAllPermutations(strs, i+1); 32 } 33 } 34 35 // 打印一个字符串的全部排列(不要出现重复的排列) 36 public static void printAllPermutations2(char[] strs, int i){ 37 if(i==strs.length){ 38 for(int t=0; t<strs.length; t++){ 39 System.out.print(strs[t]); 40 } 41 System.out.println(); 42 return; 43 } 44 Set<Character> set = new HashSet<Character>(); 45 for(int j=i; j<strs.length; j++){ 46 if(!set.contains(strs[j])){ 47 set.add(strs[j]); 48 swap(strs, i, j); 49 printAllPermutations2(strs, i+1); 50 } 51 } 52 } 53 }
母牛问题:
问题描述:
- 母牛每年生一只母牛,新出生的母牛成长三年后也能每年生一只 母牛,假设不会死。求N年后,母牛的数量
- 进阶:如果每只母牛只能活10年,求N年后,母牛的数量
思路:
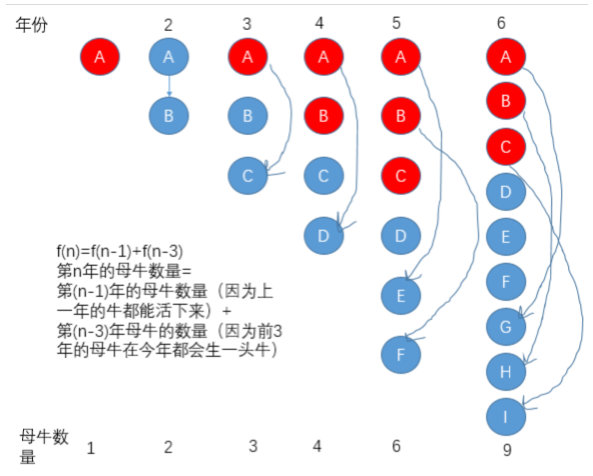
代码:
1 public class Cow { 2 // 母牛不会死的情况(递归版) 3 public static int cowNum(int n) { 4 if (n < 1) { 5 return 0; 6 } 7 if (n == 1 || n == 2 || n == 3) { 8 return n; 9 } 10 return cowNum(n - 1) + cowNum(n - 3); 11 } 12 13 // 母牛不会死的情况(非递归版) 14 public static int cowNum2(int n) { 15 if (n < 1) { 16 return 0; 17 } 18 if (n == 1 || n == 2 || n == 3) { 19 return n; 20 } 21 int prepre = 1; 22 int pre = 2; 23 int res = 3; 24 int tmp1 = 0; 25 int tmp2 = 0; 26 for (int i = 4; i <= n; i++) { 27 tmp1 = pre; 28 tmp2 = res; 29 res = res + prepre; 30 prepre = tmp1; 31 pre = tmp2; 32 } 33 return res; 34 } 35 36 // 母牛只能活10年 37 public static int cowNum3(int n) { 38 if (n < 1) { 39 return 0; 40 } 41 if (n == 1 || n == 2 || n == 3) { 42 return n; 43 } 44 if (n <= 10) { 45 return cowNum3(n - 1) + cowNum3(n - 3); 46 } 47 if (n<=14){ 48 return cowNum3(n - 1) + cowNum3(n - 3) - 2; 49 } 50 51 return cowNum3(n - 1) + cowNum3(n - 3) - 2 * (n - 13); 52 } 53 }
逆序栈
问题描述:
给你一个栈,请你逆序这个栈,不能申请额外的数据结构,只能 使用递归函数。如何实现
代码:
1 public class ReverseStackUsingRecursive { 2 // 逆序压入元素 3 public static void reverse(Stack<Integer> stack) { 4 if (stack.isEmpty()) { 5 return; 6 } 7 int i = getAndRemoveLastElement(stack); 8 reverse(stack); 9 stack.push(i); 10 } 11 12 // 返回并移除当前栈底元素 13 public static int getAndRemoveLastElement(Stack<Integer> stack) { 14 int result = stack.pop(); 15 if (stack.isEmpty()) { 16 return result; 17 } else { 18 int last = getAndRemoveLastElement(stack); 19 stack.push(result); 20 return last; 21 } 22 } 23 }
3、动态规划
(1)暴力递归改为动态规划
动态规划由暴力递归而来,是对暴力递归中的重复计算的一个优化,策略是空间换时间
什么样的递归版本可以改成动态规划:有重复状态并且重复状态与到达路径无关时可以改成动态规划
只要能写出尝试版本,那么改动态规划是高度套路的。但是不是所有的暴力递归都 能够改动态规划呢?不是的,比如汉诺塔问题和N皇后问题,他们的每一步递归都是必须的,没有多余。
这就涉及到了递归的有后效性和无后效性。 有后效性和无后效性无后效性是指对于递归中的某个子过程,其上级的决策对该级的后续决策没有任何影响。比如小路径和问题中以 下面的矩阵为例:

对于(1,1)位置上的8,无论是通过 9->1->8 还是 9->4->8 来到这个 8 上的,这个 8 到右下角的小路径和的 计算过程不会改变。这就是无后效性
注意:只有无后效性的暴力递归才能改动态规划
(2)最小路径和问题
问题描述:
给你一个二维数组,二维数组中的每个数都是正数,要求从左上角走到右下角,每一步只能向右或者向下。沿途经 过的数字要累加起来。返回小的路径和
思路:
可以用递归求解,另外可以根据递归版本改成动态规划
递归尝试:
1 // 递归尝试 2 public static int walk(int[][] matrix, int i, int j) { 3 if (i == matrix.length - 1 && j == matrix[0].length - 1) { 4 return matrix[i][j]; 5 } 6 if (i == matrix.length - 1) { 7 return matrix[i][j] + walk(matrix, i, j + 1); 8 } 9 if (j == matrix[0].length - 1) { 10 return matrix[i][j] + walk(matrix, i + 1, j); 11 } 12 int right = walk(matrix, i, j + 1); // right: 右边位置到右下角的最短路径和 13 int down = walk(matrix, i + 1, j); // down: 下边位置到右下角的最短路径和 14 return matrix[i][j] + Math.min(right, down); 15 } 16 17 public static void main(String[] args) { 18 int[][] arr = { 19 {3, 2, 1, 0}, 20 {7, 5, 0, 1}, 21 {3, 7, 6, 2} 22 }; 23 System.out.println(walk(arr, 0, 0)); 24 }
上述暴力递归的缺陷在于有些子过程是重复的。比如 walk(matrix,0,1) 和 walk(matrix,1,0) 都会依赖子过程 walk(matrix,1,1) 的状态(执行结果),那么在计算 walk(matrix,0,0) 时势 必会导致 walk(matrix,1,1) 的重复计算。
那我们能否通过对子过程计算结果进行缓存,在再次需要时直 接使用,从而实现对整个过程的一个优化呢。
由暴力递归改动态规划的核心就是将每个子过程的计算结果进行一个记录,从而达到空间换时间的目的。那么 walk(int matrix[][],int i,int j) 中变量 i 和 j 的不同取值将导致 i*j 种结果,我们将这些结果保存在一个 i*j 的表中,不就达到动态规划的目的了吗?
观察上述代码可知,有些位置上的元素是不需要尝试的(只有一种走法,不存在决策问题),因此可以直接将这些位置上的结果先算出来:

而其它位置上的元素的走法则依赖右方相邻位置(i,j+1)走到右下角的路径和和下方相邻位置(i+1,j)走 到右下角的路径和的大小比较,基于此来做一个向右走还是向左走的决策。
但由于右边界、下边界位置上的结 果我们已经计算出来了,因此对于其它位置上的结果也就不难确定了:
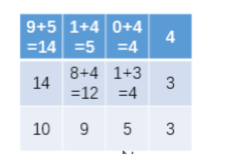
从 base case 开始,倒着推出了所有子过程的计算结果,并且没有重复计算。后 walk(matrix,0,0) 也就解出来了
这就是动态规划,它不是凭空想出来的。首先我们尝试着解决这个问题,写出了暴力递归。再由暴力递归中 的变量的变化范围建立一张对应的结果记录表,以 base case 作为突破口确定能够直接确定的结果,后解决普遍情况对应的结果
动态规划:
1 // 动态规划 2 public static int walk2(int[][] m) { 3 if (m == null || m.length == 0 || m[0] == null || m[0].length == 0) { 4 return 0; 5 } 6 int row = m.length; 7 int col = m[0].length; 8 int[][] dp = new int[row][col]; 9 dp[0][0] = m[0][0]; 10 for (int i = 1; i < row; i++) { 11 dp[i][0] = dp[i - 1][0] + m[i][0]; 12 } 13 for (int i = 1; i < col; i++) { 14 dp[0][i] = dp[0][i-1] + m[0][i]; 15 } 16 for(int i=1; i<row; i++){ 17 for(int j=1; j<col; j++){ 18 dp[i][j] = Math.min(dp[i-1][j], dp[i][j-1]) + m[i][j]; 19 } 20 } 21 return dp[row-1][col-1]; 22 }
(3)一个数是否是数组中任意个数的和
问题描述:
给你一个数组arr,和一个整数aim。如果可以任意选择arr中的数字,能不能累加得到aim,返回true或者false
思路:
跟求解一个字符串的所有子序列的思路一致,穷举出数组中所有任意个数相加的不同结果(每个数要么要要么不要)
递归尝试:
1 public static boolean isSum(int[] arr, int i, int sum, int aim) { 2 if (i == arr.length) { 3 return sum == aim; 4 } 5 return isSum(arr, i + 1, sum, aim) || isSum(arr, i + 1, sum + arr[i], aim); 6 }
上述递归函数的参数,找出变量。这里 arr 和 aim 是固定不变的,可变的只有 sum 和 i
对应变量的变化范围建立一张表保存不同子过程的结果,这里 i 的变化范围是 0~arr.length-1 , 而 sum 的变化范围是 0~数组元素总和
从 base case 入手,计算可直接计算的子过程,以 isSum(0, 0, 5) 的计算为例,其子过程中“是否+3”的决策 之后的结果是可以确定的:
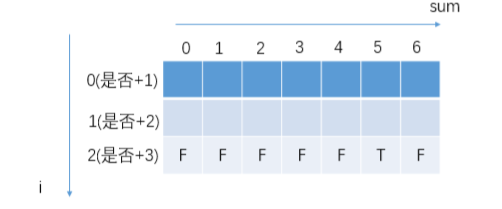
按照递归函数中 base case 下的尝试过程,推出其它子过程的计算结果,这里以 i=1,sum=1 的推导为例:
i=1 sum=1 =》isSum(arr, i+1, sum, aim) || isSum(arr, i+1, sum, aim)
= isSum(arr, 2, 1+2, aim) || isSum(arr, 2, 1, aim) (要么加2要么不加2)
= (i=2, sum=3) || (i=2, sum=1) (继续往下算)
= false || false = false
动态规划:
1 public static boolean isSum2(int[] arr, int aim) { 2 int sum = 0; 3 int len = arr.length; 4 for (int i = 0; i < len; i++) { 5 sum += arr[i]; 6 } 7 if (sum < aim) { 8 return false; 9 } 10 boolean[][] dp = new boolean[len + 1][sum + 1]; 11 for (int i = 0; i < dp.length; i++) { 12 dp[i][aim] = true; 13 } 14 for (int i = len - 1; i >= 0; i--) { 15 for (int j = aim - 1; j >= 0; j--) { 16 // dp[i][j] = dp[i+1][j] || dp[i+1][j+arr[i]]; 17 dp[i][j] = dp[i + 1][j]; 18 if (j + arr[i] <= aim) { 19 dp[i][j] = dp[i][j] || dp[i + 1][j + arr[i]]; 20 } 21 } 22 } 23 24 return dp[0][0]; 25 }
总结暴力递归改动态规划:
- 写出暴力尝试版本
- 判断是否可以改成动态规划(是否具有无后效性)
- 分析递归函数的可变参数(那几个是可变参数、可变范围)
- 可变参数的个数和范围决定矩阵的维度和范围(将最终状态表示在矩阵中)
- 把递归函数中的base case计算出来然后在矩阵中放在对应的位置
- 矩阵中的普遍位置根据递归函数中的递推式计算(逆着回去就是填表的顺序)