T1
思路
乍一看上去似乎是个签到题。然而分数低的可怜。以为小写字母的ASCII码会比100小,开个100的数组足够了。结果忘了'a'就已经是96了。凉凉
题目有一个坑点就是,如果知道了25个字母所对应的字母,那么另外一个也是可以推出来的。
代码
#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
typedef long long ll;
const int N = 1010;
int bz[233];
ll read(){
ll x = 0, f = 1;
char c = getchar();
while(c < '0' || c > '9') {
if(c == '-') f = -1;
c = getchar();
}
while(c >= '0' && c <= '9') {
x = x * 10 + c - '0';
c = getchar();
}
return x * f;
}
char a[N],b[N],c[N],ans[N];
int bz2[233];
int main() {
freopen("enc.in","r",stdin);
freopen("enc.out","w",stdout);
scanf("%s",a+1);
scanf("%s",b+1);
int n = strlen(a + 1);
for(int i = 1;i <= n;++i) {
if((bz[(int)b[i]] && bz[(int)b[i]] != a[i])) {
puts("ERROR");
return 0;
}
bz[(int)b[i]] = a[i];
}
int js = 0;
for(int i = 1;i <= n;++i) {
if(bz2[bz[b[i]]] == 0) {
js++;
bz2[bz[b[i]]] = 1;
}
}
if(js == 25) {
int k = 0;
for(int i = 'a';i <= 'z';++i) {
if(!bz2[i]) {
k = i;
break;
}
}
for(int i = 'a';i <= 'z';++i) {
if(!bz[i]) bz[i] = k;
}
}
scanf("%s",c+1);
int len = strlen(c+1);
for(int i = 1;i <= len;++i) {
if(!bz[(int)c[i]]) {
puts("ERROR");
return 0;
}
ans[i] = bz[(int)c[i]];
}
printf("%s",ans+1);
return 0;
}
T2
思路
显然每个数字都会与前边比自己大的数连边,一定不会与比自己小的数连边。所以这个题其实就是一个裸地最长上升子序列。
代码
#include<cstdio>
#include<algorithm>
#include<iostream>
using namespace std;
typedef long long ll;
const int N = 100000 + 100;
ll read(){
ll x = 0, f = 1;
char c = getchar();
while(c < '0' || c > '9') {
if(c == '-') f = -1;
c = getchar();
}
while(c >= '0' && c <= '9') {
x = x * 10 + c - '0';
c = getchar();
}
return x * f;
}
int a[N],ans,b[N],n;
void solve() {
for(int i = 1;i <= n;++i) {
if(a[i] > b[ans]) b[++ans] = a[i];
else {
int k = lower_bound(b+1,b+ans+1,a[i]) - b;
b[k] = a[i];
}
}
}
int main() {
freopen("sort.in","r",stdin);
freopen("sort.out","w",stdout);
n = read();
for(int i = 1;i <= n;++i) a[i] = read();
b[0] = -1;
solve();
cout<<ans;
return 0;
}
T3
思路
一开始以为又是一道水题。很开心的写了一个dfs交卷了。然后凉凉。后来仔细一思考发现自己的思路有太多bug了。因为感觉数据比较难造就没对拍23333
这个题比较容易发现的一个点(然而我并没发现)就是如果这张图里面存在一个环,那么就一定存在一个三元环。
如图
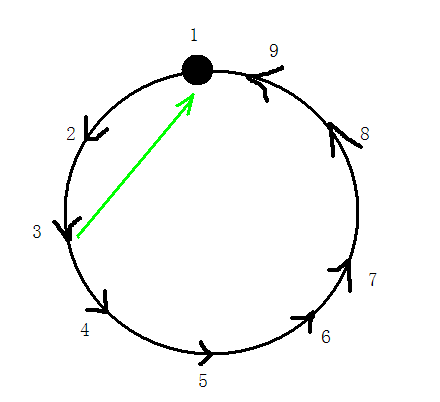
在这个环里面加入3号点指向了一号点,那么1-2-3就是一个环。如果是1指向了3,那么继续往后考虑,
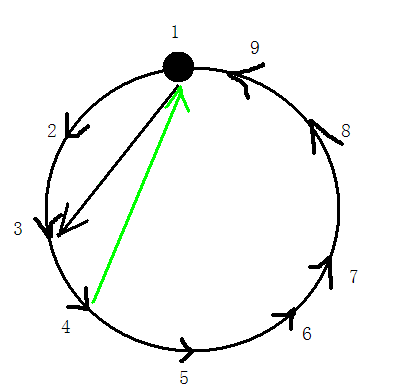
如果4连向1那么1-3-4就是一个三元环

如果1指向4,那么继续往后考虑。
不断这样下去,只要有一个点能指回一号点,那么就会存在一个三元环,如果不存在这样一个点,也就是1指向了每一个点,那么到了最后就会像上图一样,最后一条边不论怎样连都会形成一个三元环。所以结论成立

代码
#include <cstdlib>
#include <cstdio>
#include <cstring>
#include <cmath>
const int MaxN = 5005;
int n;
int mat[MaxN][MaxN];
int cycle[MaxN], cyclelen;
int stack[MaxN], stop, spos[MaxN], vis[MaxN];
bool dfs(int x) {
vis[x] = 1, stack[stop++] = x, spos[x] = stop-1;
for (int i = 0; i < n; ++i) {
if (mat[x][i]) {
if (vis[i] == 1) {
cyclelen = stop - spos[i];
memcpy(cycle, stack + spos[i], sizeof(int) * cyclelen);
return true;
} else if (vis[i] == 0) {
bool v = dfs(i);
if (v) return true;
}
}
}
--stop, vis[x] = 2;
return false;
}
void gen(void) {
int m = cyclelen;
for (int i = 1; i < m-1; ++i) {
// check 1 i i+1
if (mat[cycle[i+1]][cycle[0]]) {
printf("%d %d %d
", cycle[0]+1, cycle[i]+1, cycle[i+1]+1);
}
}
}
char tmp[MaxN];
int main(void)
{
freopen("game.in","r",stdin);
freopen("game.out","w",stdout);
scanf("%d", &n);
for (int i = 0; i < n; ++i) {
scanf("
%s", tmp);
for (int j = 0; j < n; ++j) {
mat[i][j] = tmp[j] == '1';
}
}
for (int i = 0; i < n; ++i) {
if (vis[i] == 0) {
bool found = dfs(i);
if (found) {
gen();
return 0;
}
}
}
printf("-1
");
fclose(stdin);
fclose(stdout);
return 0;
}
本题的图片转自:hwim
总结
期望得分:100 + 100 + 80 = 280
实际得分:50 + 100 + 30 = 180
太不细心了。还是有很多细节出错。再就是对拍真的很重要
一言
一直保持微笑是有诀窍的,那就是,在想哭的时候放声大哭。 ——天使领域