定义
树的直径就是指树上的最长路径。一棵树可能有多个直径,并且这些直径一定两两相交。
性质
性质1
从树上的任何一个点为起点,所找到的最长路径的的终点一定是直径的一个端点。
证明:
考虑反证法。
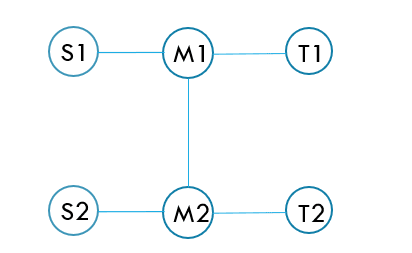
①假设直径与最长路径没有交集
用(dist(x,y))表示从(x)到(y)的距离。(dist(S1,T1))是直径。(dist(S2,T2))是从(S2)出发的最长路径。
因为(dist(S1,T1) > dist(S2,T2))(如果相等,(dist(S2,T2))也是一条直径,已经满足目的),所以(dist(S1,M1))与(dist(M1,T1))中一定有一个大于(dist(M2,T2))。
所以一定有(dist(S2,S1) > dist(S2,T2))或者(dist(S2,T1) > dist(S2,T2))。
与(dist(S2,T2))是最长路径矛盾。所以直径与最长路径一定有交集
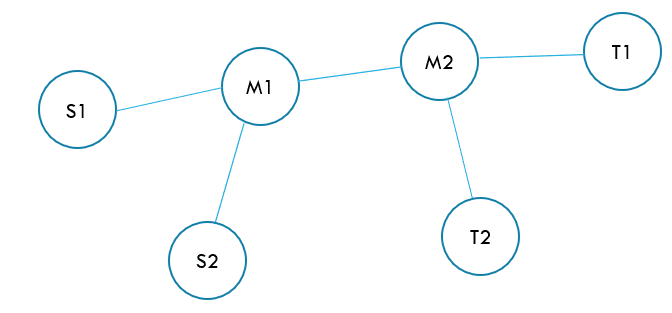
②假设最长路径的终点不是直径的端点。
如图,同样(dist(S1,T1))是直径。(dist(S2,T2))是从(S2)出发的最长路径。
如果(dist(M2,T1)<dist(M2,T2)),那么肯定有(dist(S1,T1)< dist(S1,T2)),与(dist(S1,T1))是直径矛盾。
如果(dist(M2,T1) > dist(M2,T2)),那么肯定有(dist(S2,T1) > dist(S2,T2)),与(dist(S2,T2))是从(S2)开始的最长路径矛盾。
如果(dist(M2,T1) = dist(M2,T2)),那么(dist(S2,T2))肯定也是一条直径。那么就已经满足最长路径的终点是直径的一个端点了。
所以最长路径的终点一定是直径的一个端点。
性质2
用一条边将两棵树连接成为一棵树,新树的直径的两个端点一定是原来的两条直径的四个端点中的两个。
证明:
分情况讨论
①直径不经过新边
这个时候显然是原本两条直径中的一条。
②直径经过新边
新边两端分属两棵树,那么这条直径的新边两端部分肯定是从这两个点出发在各自树中的最长路径。根据定理5,端点还是四个端点之二!
求树的直径
有两种方法
方法1
根据性质(1),先从任意一个点(dfs)一遍。找到直径的一个端点,然后这个端点出发,再(dfs)一遍,找到直径。
方法2
树型dp的方法。用(f[i])表示以i为根的子树中的直径长度。(g[i])表示i的子树中距离根最远的点的距离。
直径有三种来源,既可以从每个儿子的(f[v])中取(max),也可以将(g[u])的最大值和次大值相加。
这种做法可以把顺带求出每棵子树的直径。
代码
方法1
/*
* @Author: wxyww
* @Date: 2019-01-29 11:19:15
* @Last Modified time: 2019-01-29 14:07:48
*/
#include<cstdio>
#include<iostream>
#include<cstdlib>
#include<cmath>
#include<ctime>
#include<bitset>
using namespace std;
typedef long long ll;
const int N = 10000;
ll read() {
ll x=0,f=1;char c=getchar();
while(c<'0'||c>'9') {
if(c=='-') f=-1;
c=getchar();
}
while(c>='0'&&c<='9') {
x=x*10+c-'0';
c=getchar();
}
return x*f;
}
struct node {
int v,w,nxt;
}e[N << 1];
int head[N],re,ejs,ans;
void add(int u,int v,int w) {
e[++ejs].v = v;e[ejs].w = w;e[ejs].nxt = head[u];head[u] = ejs;
}
void dfs(int u,int father,int now) {
for(int i = head[u];i;i = e[i].nxt) {
int v = e[i].v;
if(v == father) continue;
dfs(v,u,now + e[i].w);
}
if(now > ans) re = u,ans = now;
}
int main() {
int n = read();
for(int i = 1;i < n;++i) {
int u = read(),v = read(),w = read();
add(u,v,w);add(v,u,w);
}
dfs(1,0,0);
ans = 0;
dfs(re,0,0);
cout<<ans;
return 0;
}
方法2
/*
* @Author: wxyww
* @Date: 2019-01-29 11:38:02
* @Last Modified time: 2019-01-29 14:14:17
*/
#include<cstdio>
#include<iostream>
#include<cstdlib>
#include<cmath>
#include<ctime>
#include<bitset>
using namespace std;
typedef long long ll;
const int N = 10000 + 100;
ll read() {
ll x=0,f=1;char c=getchar();
while(c<'0'||c>'9') {
if(c=='-') f=-1;
c=getchar();
}
while(c>='0'&&c<='9') {
x=x*10+c-'0';
c=getchar();
}
return x*f;
}
int f[N],gmx[N],gcmx[N];
struct node {
int v,nxt,w;
}e[N << 1];
int head[N],ejs;
void add(int u,int v,int w) {
e[++ejs].v = v;e[ejs].w = w;e[ejs].nxt = head[u];head[u] = ejs;
}
void dfs(int u,int father) {
for(int i = head[u];i;i = e[i].nxt) {
int v = e[i].v;
if(v == father) continue;
dfs(v,u);
int k = gmx[v] + e[i].w;
if(k > gmx[u]) {
gcmx[u] = gmx[u];
gmx[u] = k;
}
else if(k > gcmx[u]) gcmx[u] = k;
f[u] = max(f[u],f[v]);
}
f[u] = max(f[u],gmx[u] + gcmx[u]);
}
int main() {
int n = read();
for(int i = 1;i < n;++i) {
int u = read(),v = read(),w = read();
add(u,v,w);add(v,u,w);
}
dfs(1,0);
cout<<f[1];
return 0;
}