剑指offer26：将二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点，只能调整树中结点指针的指向。

1 题目描述

　　输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点，只能调整树中结点指针的指向。

2 思路和方法

　　在二叉搜索树中，每个结点都有两个分别指向其左、右子树的指针，左子树结点的值总是小于父结点的值，右子树结点的值总是大于父结点的值。

　　在双向链表中，每个结点也有两个指针，它们分别指向前一个结点和后一个结点。

　　所以这两种数据结构的结点是一致，二叉搜索树和双向链表，只是因为两个指针的指向不同而已举个例子，如下图中的二叉搜索树，转换后的双向链表为：

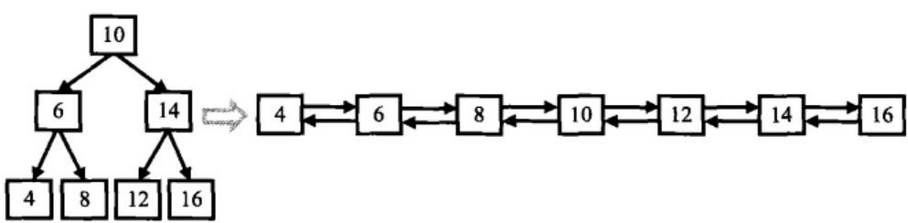
　　思路：

　　为了减少指针的变换次数，并让操作更加简单，在转换成排序双向链表时，原先指向左子结点的指针调整为链表中指向前一个结点的指针，原先指向右子结点的指针调整为链表中指向下一个结点的指针。
由于要求链表是有序的，可以借助二叉树中序遍历，因为中序遍历算法的特点就是从小到大访问结点。当遍历访问到根结点时，假设根结点的左侧已经处理好，只需将根结点与上次访问的最近结点（左子树中最大值结点）的指针连接好即可。进而更新当前链表的最后一个结点指针。

　　方法：

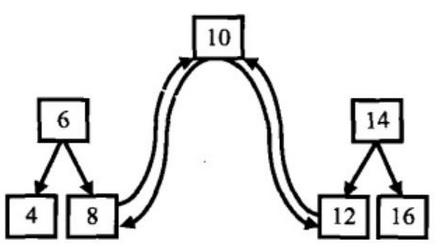
　　如上图的二叉排序树，就分成了根结点10、以结点6为根的左子对和以结点14为根的右子树。从变换的链表中我们可以看到，应当把结点10的left指针指向结点8，把结点8的right指针指向结点10，而由于我们采用的是中序遍历，所以当我们遍历到结点10时，结点10的左子树已经转化为一个有序的双向链表，而结点8是这个已经转化的双向链表的尾结点，所以我们应该用一个变量last_node来保存最后一个结点的指针，以便在与根结点连续时使用。然后把这个变量last_node的值更新为指向根结点10。对于结点10的右子树，采取相似的操作。

3 C++核心代码

/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};*/
class Solution {
public:
    TreeNode* Convert(TreeNode* pRootOfTree)
    {
        stack<TreeNode*> st;
        TreeNode *cur = pRootOfTree;     //为临时节点用来遍历树的节点，初始值为根节点root
        TreeNode *pre = pRootOfTree;    // 用于保存中序遍历序列的上一节点
        TreeNode *head = pRootOfTree;    //用于记录双向链表的头结点
        bool isFirst = true;         //判断是否为左子树链表的第一个节点
        while(cur||!st.empty())
        {
            while(cur)
            {
                st.push(cur);
                cur = cur->left;
            }
            cur = st.top();    //此时的cur为左子树最左边的节点
            st.pop();
            if(isFirst)    //假如是左子树链表的第一个节点
            {   //将cur赋值给root节点
                head = pre = cur;    //将中序遍历序列中的第一个节点记为根节点(root node)
                isFirst = false;
            }
            else
            {
                pre->right = cur;
                cur->left = pre;
                pre = cur;
            }
            cur = cur->right;
        }
        return head;
    }
};

4 C++完整代码

#include<iostream>
using namespace std;

//二叉树结点定义
struct BinaryTreeNode
{
    int Value;
    BinaryTreeNode* Left;
    BinaryTreeNode* Right;
};

//创建二叉树结点
BinaryTreeNode* CreateBinaryTreeNode(int value)
{
    BinaryTreeNode* pNode = new BinaryTreeNode();
    pNode->Value = value;
    pNode->Left = NULL;
    pNode->Right = NULL;
    return pNode;
}

//连接树结点
void ConnectTreeNodes(BinaryTreeNode* pParent, BinaryTreeNode* pLeft, BinaryTreeNode* pRight)
{
    if (pParent != NULL)
    {
        pParent->Left = pLeft;
        pParent->Right = pRight;
    }
}

//中序遍历
void InOrderPrintTree(BinaryTreeNode* pRoot)
{
    if (pRoot != NULL)
    {
        //遍历左边
        if (pRoot->Left != NULL)
        {
            InOrderPrintTree(pRoot->Left);
        }
        //根
        cout << "value of this node is " << pRoot->Value << endl;
        //遍历右边
        if (pRoot->Right != NULL)
        {
            InOrderPrintTree(pRoot->Right);
        }

    }
    else
    {
        cout << "this node is null." << endl;
    }

}

//转换排序二叉树为双向链表
void Convert(BinaryTreeNode* pNode, BinaryTreeNode** pLastNodeLnList)
{
    if (pNode == NULL)
    {
        return;
    }

    BinaryTreeNode* pCurrent = pNode;

    //左子树转换，遍历到左子树的叶子结点
    if (pCurrent->Left != NULL)
    {
        Convert(pCurrent->Left, pLastNodeLnList);
    }
    pCurrent->Left = *pLastNodeLnList;
    if ((*pLastNodeLnList) != NULL)
    {
        (*pLastNodeLnList)->Right = pCurrent;
    }
    *pLastNodeLnList = pCurrent;

    //右子树转换
    if (pCurrent->Right != NULL)
    {
        Convert(pCurrent->Right, pLastNodeLnList);
    }

}

//获取双向链表头结点
BinaryTreeNode* Convert(BinaryTreeNode* pRoot)
{
    //指向双向链表的尾结点
    BinaryTreeNode* pLastNodeInList = NULL;
    //转换排序二叉树为双向链表
    Convert(pRoot, &pLastNodeInList);

    //求双向链表的头结点
    BinaryTreeNode* pHeadOfList = pLastNodeInList;
    while (pHeadOfList != NULL&&pHeadOfList->Left != NULL)
    {
        pHeadOfList = pHeadOfList->Left;
    }
    return pHeadOfList;
}

//打印双向链表
void PrintList(BinaryTreeNode* pRoot)
{
    BinaryTreeNode* pNode = pRoot;

    while (pNode != NULL)
    {
        cout << pNode->Value << "    ";
        pNode = pNode->Right;
    }

    cout << endl;
    cout << "PrintList ends." << endl << endl;

}


// ====================测试代码====================
void Test1()
{
    //                 10
    //              /      
    //            6        14
    //           /        /  
    //          4  8      12  16

    cout << "The Test1:" << endl;

    //创建树结点
    BinaryTreeNode* pNode10 = CreateBinaryTreeNode(10);
    BinaryTreeNode* pNode6 = CreateBinaryTreeNode(6);
    BinaryTreeNode* pNode14 = CreateBinaryTreeNode(14);
    BinaryTreeNode* pNode4 = CreateBinaryTreeNode(4);
    BinaryTreeNode* pNode8 = CreateBinaryTreeNode(8);
    BinaryTreeNode* pNode12 = CreateBinaryTreeNode(12);
    BinaryTreeNode* pNode16 = CreateBinaryTreeNode(16);

    //连接树结点
    ConnectTreeNodes(pNode10, pNode6, pNode14);
    ConnectTreeNodes(pNode6, pNode4, pNode8);
    ConnectTreeNodes(pNode14, pNode12, pNode16);

    //中序遍历
    InOrderPrintTree(pNode10);
    //获取双向链表头结点
    BinaryTreeNode* pHeadOfList = Convert(pNode10);
    //输出链表
    PrintList(pHeadOfList);

}

void Test2()
{
    //               5
    //              /
    //             4
    //            /
    //           3
    //          /
    //         2
    //        /
    //       1

    cout << "The Test2:" << endl;
    //创建树结点
    BinaryTreeNode* pNode5 = CreateBinaryTreeNode(5);
    BinaryTreeNode* pNode4 = CreateBinaryTreeNode(4);
    BinaryTreeNode* pNode3 = CreateBinaryTreeNode(3);
    BinaryTreeNode* pNode2 = CreateBinaryTreeNode(2);
    BinaryTreeNode* pNode1 = CreateBinaryTreeNode(1);

    //连接树结点
    ConnectTreeNodes(pNode5, pNode4, NULL);
    ConnectTreeNodes(pNode4, pNode3, NULL);
    ConnectTreeNodes(pNode3, pNode2, NULL);
    ConnectTreeNodes(pNode2, pNode1, NULL);

    //中序遍历
    InOrderPrintTree(pNode5);
    //获取双向链表头结点
    BinaryTreeNode* pHeadOfList = Convert(pNode5);
    //输出链表
    PrintList(pHeadOfList);

}

void Test3()
{
    // 1
    //  
    //   2
    //    
    //     3
    //      
    //       4
    //        
    //         5

    cout << "The Test3:" << endl;
    //创建树结点
    BinaryTreeNode* pNode1 = CreateBinaryTreeNode(1);
    BinaryTreeNode* pNode2 = CreateBinaryTreeNode(2);
    BinaryTreeNode* pNode3 = CreateBinaryTreeNode(3);
    BinaryTreeNode* pNode4 = CreateBinaryTreeNode(4);
    BinaryTreeNode* pNode5 = CreateBinaryTreeNode(5);

    //连接树结点
    ConnectTreeNodes(pNode1, NULL, pNode2);
    ConnectTreeNodes(pNode2, NULL, pNode3);
    ConnectTreeNodes(pNode3, NULL, pNode4);
    ConnectTreeNodes(pNode4, NULL, pNode5);

    //中序遍历
    InOrderPrintTree(pNode1);
    //获取双向链表头结点
    BinaryTreeNode* pHeadOfList = Convert(pNode1);
    //输出链表
    PrintList(pHeadOfList);

}

void Test4()
{
    // 树中只有1个结点

    cout << "The Test4:" << endl;
    //创建树结点
    BinaryTreeNode* pNode1 = CreateBinaryTreeNode(1);

    //连接树结点
    ConnectTreeNodes(pNode1, NULL, NULL);

    //中序遍历
    InOrderPrintTree(pNode1);
    //获取双向链表头结点
    BinaryTreeNode* pHeadOfList = Convert(pNode1);
    //输出链表
    PrintList(pHeadOfList);

}

void Test5()
{
    // 树中没有结点

    cout << "The Test5:" << endl;
    //创建树结点
    BinaryTreeNode* pNode1 = CreateBinaryTreeNode(NULL);

    //连接树结点
    ConnectTreeNodes(pNode1, NULL, NULL);

    //中序遍历
    InOrderPrintTree(pNode1);
    //获取双向链表头结点
    BinaryTreeNode* pHeadOfList = Convert(pNode1);
    //输出链表
    PrintList(pHeadOfList);

}

void main()
{
    Test1();
    Test2();
    Test3();
    Test4();
    Test5();
    system("pause");
}

参考资料

https://blog.csdn.net/u012477435/article/details/83351659

https://blog.csdn.net/yanxiaolx/article/details/52073221

https://blog.csdn.net/jyy305/article/details/76383723（Solution中函数不同时）

https://blog.csdn.net/ljianhui/article/details/22338405（完整代码另一个版本）