剑指offer4：重建二叉树（后序遍历）

1. 题目描述

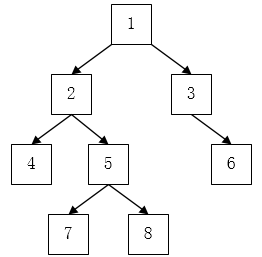
　　输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。

2. 思路和方法

　　（1）先序遍历序列的第一个元素必定是根节点，可以由此获取二叉树的根节点。

　　（2）根据根节点，中序遍历序列中查找该节点，由中序遍历的性质可知，中序遍历中该根节点左边的序列必定在根节点的左子树中，根节点右边的序列必定在右子树中。由此可以知道先序遍历中左子树以及右子树的起止位置。

　　（3）分别对左子树和右子树重复上述的过程，直至所有的子树的起止位置相等时，说明已经到达叶子节点，遍历完毕。
　　（4）先序+中序->后序，中序+后序->先序，层次+中序->。

例子：

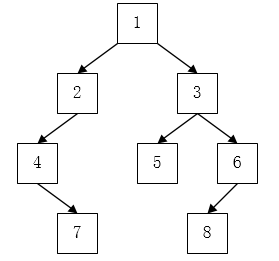
　　先序遍历：1 2 4 5 7 8 3 6 （根左右）

　　中序遍历：4 2 7 5 8 1 3 6（左根右）

　　后序遍历：4 7 8 5 2 6 3 1（左右根）

　　层次遍历：1 2 3 4 5 6 7 8 （共4层，与广度搜索一样，即广度遍历）

特殊例子：

先序遍历：1, 2, 4, 7, 3, 5, 6, 8 （根左右）

中序遍历：4, 7, 2, 1, 5, 3, 8, 6 （左根右）

后序遍历：7 4 2 5 8 6 3 1（左右根）

层次遍历：1 2 3 4 5 6 7 8 （共4层，与广度搜索一样，即广度遍历）

3. 核心代码

 1 /**
 2  * Definition for binary tree
 3  * struct TreeNode {
 4  *     int val;
 5  *     TreeNode *left;
 6  *     TreeNode *right;
 7  *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 8  * };
 9  */
10 class Solution {
11 public:
12     TreeNode* reConstructBinaryTree(vector<int> pre,vector<int> vin) {
13         int len=vin.size();
14         if (len==0)
15             return NULL;
16         vector<int> left_pre,right_pre,left_vin,right_vin;
17         TreeNode* head = new TreeNode(pre[0]);
18         int gen = 0;
19         for(int i=0;i<len;i++)
20         {
21             if(vin[i]==pre[0])
22             {
23                 gen = i;
24                 break;
25             }
26         }
27         for(int i=0;i<gen;i++)
28         {
29             left_pre.push_back(pre[i+1]);
30             left_vin.push_back(vin[i]);
31         }
32         for(int i=gen+1;i<len;i++)
33         {
34             right_pre.push_back(pre[i]);
35             right_vin.push_back(vin[i]);
36         }
37         head->left = reConstructBinaryTree(left_pre,left_vin);
38         head->right = reConstructBinaryTree(right_pre,right_vin);
39         return head;
40     }
41 };

View Code

4. C++完整实现

  1 #include <vector>
  2 #include <iostream>
  3 #include <string>
  4 #include <stdlib.h>
  5 #include <algorithm>
  6 
  7 using namespace std;
  8 
  9 struct TreeNode {
 10     int val;
 11     TreeNode *left;
 12     TreeNode *right;
 13     TreeNode(int x) :val(x), left(nullptr), right(nullptr) {}
 14 } ;
 15 
 16 //打印节点/访问函数  
 17 void PrintNode(TreeNode* T)
 18 {
 19     if (T->val != -1)
 20         cout << T->val << " ";
 21 }
 22 
 23 //先序遍历  
 24 void PreOrder(TreeNode* T)
 25 {
 26     if (T != NULL)
 27     {
 28         //访问根节点  
 29         PrintNode(T);
 30         //访问左子结点  
 31         PreOrder(T->left);
 32         //访问右子结点  
 33         PreOrder(T->right);
 34     }
 35 }
 36 
 37 //中序遍历
 38 void InOrder(TreeNode* T)
 39 {
 40     if (T != NULL)
 41     {
 42         //访问左子结点
 43         InOrder(T->left);
 44         //访问根节点
 45         PrintNode(T);
 46         //访问右子结点
 47         InOrder(T->right);
 48     }
 49 }
 50 
 51 //后序遍历
 52 void PostOrder(TreeNode* T)
 53 {
 54     if (T != NULL)
 55     {
 56         //访问左子结点
 57         PostOrder(T->left);
 58         //访问右子结点
 59         PostOrder(T->right);
 60         //访问根节点
 61         PrintNode(T);
 62     }
 63 }
 64 
 65 TreeNode* reConstructBinaryTree(vector<int> pre, vector<int> vin)
 66 {
 67     if (pre.size() == 0 || pre.size() != vin.size())
 68         return nullptr;
 69 
 70     TreeNode *newNode = new TreeNode(pre[0]);
 71     //如果只剩一个节点了，那么可以直接返回
 72     if (pre.size() == 1)
 73         return newNode;
 74 
 75     auto posi = find(vin.begin(), vin.end(), pre[0]);
 76     //错误检测
 77     if (posi == vin.end()) {
 78         return nullptr;
 79     }
 80     int leftSize = posi - vin.begin();
 81     int rightSize = vin.end() - posi - 1;
 82 
 83     //递归求解
 84     //这里取前序和后序遍历的左右子树可能有点绕，可以好好思考一下
 85     newNode->left = reConstructBinaryTree(vector<int>(pre.begin() + 1, pre.begin() + 1 + leftSize),
 86         vector<int>(vin.begin(), vin.begin() + leftSize));
 87     newNode->right = reConstructBinaryTree(vector<int>(pre.begin() + 1 + leftSize, pre.end()),
 88         vector<int>(vin.begin() + leftSize + 1, vin.end()));
 89 
 90     return newNode;
 91 }
 92 
 93 int main()
 94 {
 95     vector<int> pre{ 1, 2, 4, 7, 3, 5, 6, 8 };
 96     vector<int> vin{ 4, 7, 2, 1, 5, 3, 8, 6 }; ////7 4 2 5 8 6 3 1
 97 
 98     TreeNode *posTraversal = reConstructBinaryTree(pre, vin);
 99     
100     cout << "后序遍历：";
101     PostOrder(posTraversal);
102     cout << endl;
103 
104     cout << "先序遍历：";
105     PreOrder(posTraversal);
106     cout << endl;
107 
108     cout << "先序遍历：";
109     InOrder(posTraversal);
110     cout << endl;
111 
112     system("pause");
113     return 0;
114 }

View Code

5 扩展

5.1 给出中序和后序，得到二叉树

后序和先序（左右根，根左右），因此后序的根的位置为pos[pos.size()-1].

main函数中的代码如下：

cout << "给出中序和后序，构建二叉树" << endl;
//vector<int> pre{ 1, 2, 4, 7, 3, 5, 6, 8 };

vector<int> vin1{ 4, 7, 2, 1, 5, 3, 8, 6 };

vector<int> pos1{ 7, 4, 2, 5, 8, 6, 3, 1 };

TreeNode* preTraversal = reConstructBinaryTree1(pos1, vin1);

cout << "中序遍历：";

InOrder(preTraversal);

cout << endl;

C++核心代码

 1 TreeNode* reConstructBinaryTree1(vector<int> pos, vector<int> vin)
 2 {
 3     if (pos.size() == 0 || pos.size() != vin.size())
 4         return nullptr;
 5 
 6     int poslen = pos.size();
 7 
 8     TreeNode *newNode = new TreeNode(pos[poslen-1]);
 9     //如果只剩一个节点了，那么可以直接返回
10     if (poslen == 1)
11         return newNode;
12 
13     auto posi = find(vin.begin(), vin.end(), pos[poslen-1]);
14     if (posi == vin.end())
15         return nullptr;
16     int leftSize = posi - vin.begin();
17     int rightSize = vin.end() - posi - 1;
18 
19     newNode->left = reConstructBinaryTree1(vector<int>(pos.begin(), pos.begin() + leftSize), vector<int>(vin.begin(), vin.begin() + leftSize));
20     newNode->right = reConstructBinaryTree1(vector<int>(pos.begin() + leftSize, pos.end()-1), vector<int>(vin.begin() + leftSize + 1, vin.end()));
21 
22     return newNode;
23 }

View Code

5.2 给出中序和层次构建二叉树

参考资料：https://blog.csdn.net/yanyanwenmeng/article/details/77833274（一般C++程序）

参考资料：https://blog.csdn.net/sinat_30324577/article/details/82688414（Python）

核心思想：对于子树，其在层次遍历最前面的点即为根节点，故重建过程包括以下两步：
1.利用层次遍历确定子树的根节点；
2.根据根节点在中序中的位置划定左右子树，递归重建。

一般C++程序

 1 #include<iostream>
 2 #include<string>
 3 
 4 using namespace std;
 5 string s1, s2;
 6 void calc(int l1, int r1, int l2, int r2)
 7 {
 8     int i, j;
 9     for (i = l2; i <= r2; i++)//找层次遍历中优先输出根节点的位置 
10     {
11         int b = 0;
12         for (j = l1; j <= r1; j++)
13         {
14             if (s2[i] == s1[j])
15             {
16                 cout << s1[j];//输出根节点 
17                 b = 1;
18                 break;
19             }
20         }
21         if (b) break;
22     }
23     if (j>l1) calc(l1, j - 1, 0, r2);//遍历左子树 
24     if (j<r1) calc(j + 1, r1, 0, r2);//遍历右子树 
25 }
26 int main()
27 {
28     cin >> s1 >> s2;
29     calc(0, s1.length() - 1, 0, s2.length() - 1);
30     cout << endl;
31     return 0;
32 }

View Code

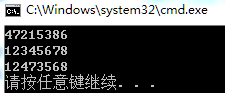
运行：输入输出

C++核心程序（vector<int>）

 1 TreeNode* reConstructBinaryTree2(vector<int> level, vector<int> vin)
 2 {
 3     if (level.size() == 0 || vin.size() == 0)
 4         return nullptr;
 5     vector<int> lst;
 6     for (int i = 0; i < vin.size(); i++){
 7         lst.push_back(find(level.begin(), level.end(), vin[i]) - level.begin());
 8     }
 9     int minPosition = min_element(lst.begin(), lst.end()) - lst.begin();
10 
11     cout << "vin[minPosition]=" << vin[minPosition] << endl;
12     TreeNode *newNode = new TreeNode(vin[minPosition]);
13 
14     newNode->left = reConstructBinaryTree2(vector<int>(level.begin(), level.end()),
15         vector<int>(vin.begin(), vin.begin() + minPosition));
16     newNode->right = reConstructBinaryTree2(vector<int>(level.begin(), level.end()),
17         vector<int>(vin.begin() + minPosition + 1, vin.end()));
18     
19     return newNode;
20 ｝

View Code

输出：

6. 二叉树构建参考资料：用先序构建，https://blog.csdn.net/u014453898/article/details/54894796

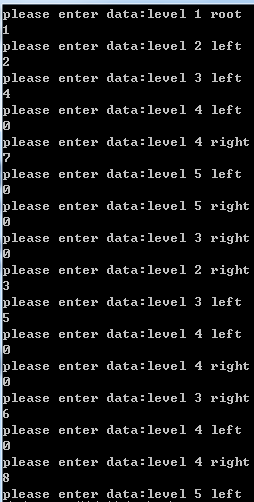
C++代码

 1 #include<iostream>
 2 
 3 #include<string> 
 4 using namespace std;
 5 
 6 /*二叉树的结构体*/
 7 typedef struct BTree
 8 {
 9     int val;
10     struct BTree *left, *right;
11 }BTree;
12 
13 /*二叉树的类，包含着操作二叉树的各种方法*/
14 class Tree
15 {
16 public:
17     BTree *create_node(int level, string pos);
18     void PreOrder(BTree *t);  //先序遍历 
19     void InOrder(BTree *t);  //中序遍历 
20     void PostOrder(BTree *t);  //后序遍历 
21 
22     BTree *root;
23 };
24 
25 /*用先序遍历的方法递归构造一课二叉树*/
26 BTree* Tree::create_node(int level, string pos)
27 {
28     int data;
29     BTree *node = new BTree;
30 
31     cout << "please enter data:level " << level << " " << pos << endl;
32     cin >> data;
33 
34     //若输入的数据为0，则把该结点的子结点置为空 
35     if (data == 0)
36     {
37         return NULL;
38     }
39 
40     node->val = data;
41 
42     /*create_node（）的    参数用于在给二叉树赋值时表明
43     现在赋值的是哪个结点*/
44     node->left = create_node(level + 1, "left");
45     node->right = create_node(level + 1, "right");
46     return node;
47 }
48 
49 void Tree::PreOrder(BTree *t)
50 {
51     if (t)
52     {
53         cout << t->val << endl;;
54         PreOrder(t->left);
55         PreOrder(t->right);
56     }
57 }
58 
59 void Tree::InOrder(BTree *t)
60 {
61     if (t)
62     {
63         InOrder(t->left);
64         cout << t->val << endl;;
65         InOrder(t->right);
66     }
67 }
68 
69 void Tree::PostOrder(BTree *t)
70 {
71     if (t)
72     {
73         PostOrder(t->left);
74         PostOrder(t->right);
75         cout << t->val << endl;
76     }
77 }
78 
79 int main()
80 {
81     Tree tree;
82     tree.root = tree.create_node(1, "root");
83     cout << "Pre" << endl;
84     tree.PreOrder(tree.root);
85 
86     cout << "In" << endl;
87     tree.InOrder(tree.root);
88 
89     cout << "Post" << endl;
90     tree.PostOrder(tree.root);
91 
92     system("pause");
93     return 0;
94 }

View Code

7. 完整C++程序

  1 #include <vector>
  2 #include <iostream>
  3 #include <string>
  4 #include <stdlib.h>
  5 #include <algorithm>
  6 
  7 using namespace std;
  8 
  9 struct TreeNode {
 10     int val;
 11     TreeNode *left;
 12     TreeNode *right;
 13     TreeNode(int x) :val(x), left(nullptr), right(nullptr) {}
 14 };
 15 
 16 //打印节点/访问函数  
 17 void PrintNode(TreeNode* T)
 18 {
 19     if (T->val != -1)
 20         cout << T->val << " ";
 21 }
 22 
 23 //先序遍历  
 24 void PreOrder(TreeNode* T)
 25 {
 26     if (T != NULL)
 27     {
 28         //访问根节点  
 29         PrintNode(T);
 30         //访问左子结点  
 31         PreOrder(T->left);
 32         //访问右子结点  
 33         PreOrder(T->right);
 34     }
 35 }
 36 
 37 //中序遍历
 38 void InOrder(TreeNode* T)
 39 {
 40     if (T != NULL)
 41     {
 42         //访问左子结点
 43         InOrder(T->left);
 44         //访问根节点
 45         PrintNode(T);
 46         //访问右子结点
 47         InOrder(T->right);
 48     }
 49 }
 50 
 51 //后序遍历
 52 void PostOrder(TreeNode* T)
 53 {
 54     if (T != NULL)
 55     {
 56         //访问左子结点
 57         PostOrder(T->left);
 58         //访问右子结点
 59         PostOrder(T->right);
 60         //访问根节点
 61         PrintNode(T);
 62     }
 63 }
 64 
 65 TreeNode* reConstructBinaryTree(vector<int> pre, vector<int> vin)
 66 {
 67     if (pre.size() == 0 || pre.size() != vin.size())
 68         return nullptr;
 69 
 70     TreeNode *newNode = new TreeNode(pre[0]);
 71     //如果只剩一个节点了，那么可以直接返回
 72     if (pre.size() == 1)
 73         return newNode;
 74 
 75     auto posi = find(vin.begin(), vin.end(), pre[0]);
 76 
 77     if (posi == vin.end())
 78         return nullptr;
 79     int leftSize = posi - vin.begin();
 80     int rightSize = vin.end() - posi - 1;
 81 
 82     newNode->left = reConstructBinaryTree(vector<int>(pre.begin() + 1, pre.begin() + 1 + leftSize), 
 83         vector<int>(vin.begin(), vin.begin() + leftSize));
 84     newNode->right = reConstructBinaryTree(vector<int>(pre.begin() + 1 + leftSize, pre.end()), 
 85         vector<int>(vin.begin() + leftSize + 1, vin.end()));
 86 
 87     return newNode;
 88 }
 89 
 90 
 91 TreeNode* reConstructBinaryTree1(vector<int> pos, vector<int> vin)
 92 {
 93     if (pos.size() == 0 || pos.size() != vin.size())
 94         return nullptr;
 95 
 96     int poslen = pos.size();
 97 
 98     TreeNode *newNode = new TreeNode(pos[poslen - 1]);
 99     //如果只剩一个节点了，那么可以直接返回
100     if (poslen == 1)
101         return newNode;
102 
103     auto posi = find(vin.begin(), vin.end(), pos[poslen - 1]);
104     if (posi == vin.end())
105         return nullptr;
106     int leftSize = posi - vin.begin();
107     int rightSize = vin.end() - posi - 1;
108 
109     newNode->left = reConstructBinaryTree1(vector<int>(pos.begin(), pos.begin() + leftSize), vector<int>(vin.begin(), vin.begin() + leftSize));
110     newNode->right = reConstructBinaryTree1(vector<int>(pos.begin() + leftSize, pos.end() - 1), vector<int>(vin.begin() + leftSize + 1, vin.end()));
111 
112     return newNode;
113 }
114 
115 TreeNode* reConstructBinaryTree2(vector<int> level, vector<int> vin)
116 {
117     if (level.size() == 0 || vin.size() == 0)
118         return nullptr;
119     vector<int> lst;
120     for (int i = 0; i < vin.size(); i++){
121         lst.push_back(find(level.begin(), level.end(), vin[i]) - level.begin());
122     }
123     int minPosition = min_element(lst.begin(), lst.end()) - lst.begin();
124 
125     //cout << "vin[minPosition]=" << vin[minPosition] << endl;
126     TreeNode *newNode = new TreeNode(vin[minPosition]);
127 
128     newNode->left = reConstructBinaryTree2(vector<int>(level.begin(), level.end()),
129         vector<int>(vin.begin(), vin.begin() + minPosition));
130     newNode->right = reConstructBinaryTree2(vector<int>(level.begin(), level.end()),
131         vector<int>(vin.begin() + minPosition + 1, vin.end()));
132     
133     return newNode;
134 //if not level or not vin :
135 //return None
136 //lst = []
137 //for num in vin :
138 //    lst.append(level.index(num))
139 //idx = lst.index(min(lst))
140 //
141 //root = TreeNode(vin[idx])
142 //left = vin[0:idx]
143 //right = vin[idx + 1:]
144 //root.left = restruct(level, left)
145 //root.right = restruct(level, right)
146 //return root
147 }
148 
149 
150 
151 int main()
152 {
153     //层次遍历是1 2 3 4 5 6 7 8
154     cout << "给出先序和中序，构建二叉树" << endl;
155     vector<int> pre0{ 1, 2, 4, 7, 3, 5, 6, 8 };
156     vector<int> vin0{ 4, 7, 2, 1, 5, 3, 8, 6 }; ////7 4 2 5 8 6 3 1
157 
158     TreeNode* posTraversal = reConstructBinaryTree(pre0, vin0);
159 
160     cout << "后序遍历：";
161     PostOrder(posTraversal);
162     cout << endl;
163 
164     cout << "先序遍历：";
165     PreOrder(posTraversal);
166     cout << endl;
167 
168     cout << "中序遍历：";
169     InOrder(posTraversal);
170     cout << endl;
171 
172 
173     cout << "给出中序和后序，构建二叉树" << endl;
174     //vector<int> pre{ 1, 2, 4, 7, 3, 5, 6, 8 };
175     vector<int> vin1{ 4, 7, 2, 1, 5, 3, 8, 6 };
176     vector<int> pos1{ 7, 4, 2, 5, 8, 6, 3, 1 };
177 
178     TreeNode* preTraversal = reConstructBinaryTree1(pos1, vin1);
179     cout << "后序遍历：";
180     PostOrder(preTraversal);
181     cout << endl;
182 
183     cout << "先序遍历：";
184     PreOrder(preTraversal);
185     cout << endl;
186 
187     cout << "中序遍历：";
188     InOrder(preTraversal);
189     cout << endl;
190 
191 
192     cout << "给出中序和层次，构建二叉树" << endl;
193     //vector<int> pre{ 1, 2, 4, 7, 3, 5, 6, 8 };
194     //vector<int> pos1{ 7, 4, 2, 5, 8, 6, 3, 1 };
195     vector<int> level2{ 1, 2, 3, 4, 5, 6, 7, 8 };
196     vector<int> vin2{ 4, 7, 2, 1, 5, 3, 8, 6 };
197     TreeNode* Traversal = reConstructBinaryTree2(level2, vin2);
198     cout << "后序遍历：";
199     PostOrder(Traversal);
200     cout << endl;
201 
202     cout << "先序遍历：";
203     PreOrder(Traversal);
204     cout << endl;
205 
206     cout << "中序遍历：";
207     InOrder(Traversal);
208     cout << endl;
209 
210 
211 
212     system("pause");
213     return 0;
214 }
215 
216 //class TreeNode : # 定义二叉树节点类
217 //    def __init__(self, val) :
218 //    self.val = val
219 //    self.left = None
220 //    self.right = None
221 //
222 //    def restruct(level, vin) :
223 //if not level or not vin :
224 //return None
225 //lst = []
226 //    for num in vin :
227 //    lst.append(level.index(num))
228 //        print("lst" + str(lst))
229 //        idx = lst.index(min(lst))
230 //        print("idx--" + str(idx))
231 //
232 //        root = TreeNode(vin[idx])
233 //        left = vin[0:idx]
234 //        right = vin[idx + 1:]
235 //        root.left = restruct(level, left)
236 //        root.right = restruct(level, right)
237 //        return root
238 //
239 //        lst1 = []
240 //        lst2 = []
241 //
242 //        def pre_traverse(root) :
243 //    if not root :
244 //    return None
245 //        lst1.append(root.val)
246 //        pre_traverse(root.left)
247 //        pre_traverse(root.right)
248 //        return lst1
249 //
250 //        def leaf(root) :
251 //    if not root :
252 //    return None
253 //    if not root.left and not root.right :
254 //        lst2.append(root.val)
255 //        leaf(root.left)
256 //        leaf(root.right)
257 //        return lst2
258 //
259 //        b = restruct([1, 2, 3, 4, 5, 6, 7, 8], [4, 7, 2, 1, 5, 3, 8, 6])
260 //
261 //        print(pre_traverse(b))

View Code

参考资料

https://blog.csdn.net/My_Jobs/article/details/43451187

https://blog.csdn.net/wtyvhreal/article/details/45644843

https://blog.csdn.net/m0_37950361/article/details/82531649

https://blog.csdn.net/u014453898/article/details/54894796

https://blog.csdn.net/sinat_30324577/article/details/82688414

相关阅读:
export default 和 export 的使用方式（六）
webpack结合vue使用（五）
webpack 中导入 vue 和普通网页使用 vue 的区别（四）
普通组件定义渲染和render渲染组件的区别（三）
代码规范
 vue切换路由时，取消所有axios请求
 JS设计模式-策略模式
 CSS世界(张鑫旭)系列学习总结（五）内联元素与流
 Vue中Jsx的使用
 Vue事件总线（EventBus）
原文地址：https://www.cnblogs.com/wxwhnu/p/11390471.html