两个流程:训练字典+重建。
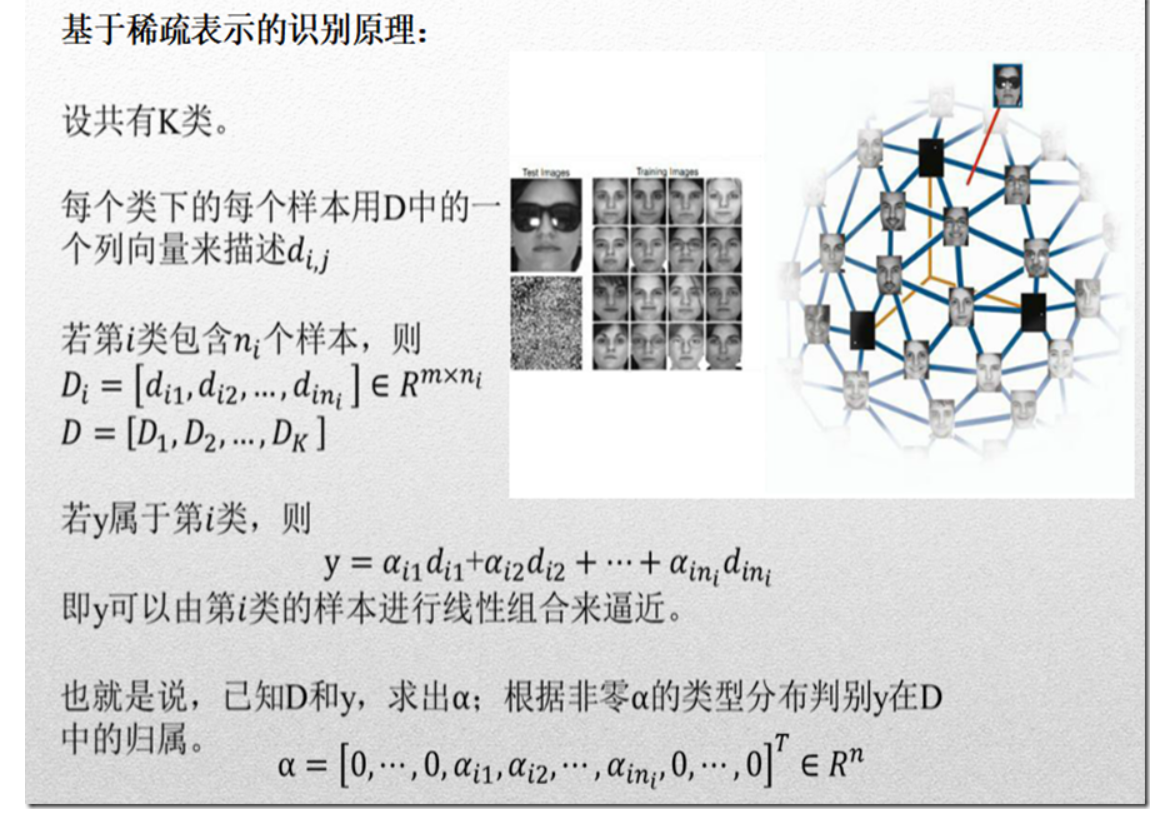
相关:L1、L2范数
L1使权值稀疏。L2防过拟合。
L1范数可以使权值稀疏,方便特征提取。 L2范数可以防止过拟合,提升模型的泛化能力。
L1和L2正则先验分别服从的分布:L1是拉普拉斯分布,L2是高斯分布。
L0 范数是 ||x||0 = xi (xi不等于0)代表非0元素的个数,[1,2,3,4,5] 非0个数为5,[0,1,2,0,3]非0 个数为3。
L1范数是||x||1=Σ|xi| x与0之间的曼哈顿距离,[1,2,3,-2,-1] =1+2+3+2+1 =9,为个数字的绝对值的和。
L2范数是||x||2=Σ|xi|^2为x与0之间的欧式距离,[1,2,-3]=1^2+2^2+(-3)^2=1+4+9=14,为各个数字的平方和在开方。
Lp范数是||x||p=√∑(xi)^p。控制模型复杂度减少过拟合。一般在损失函数中加入惩罚项。
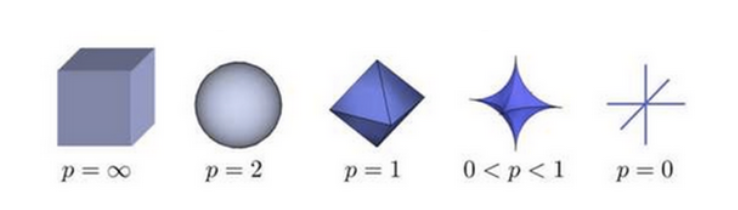
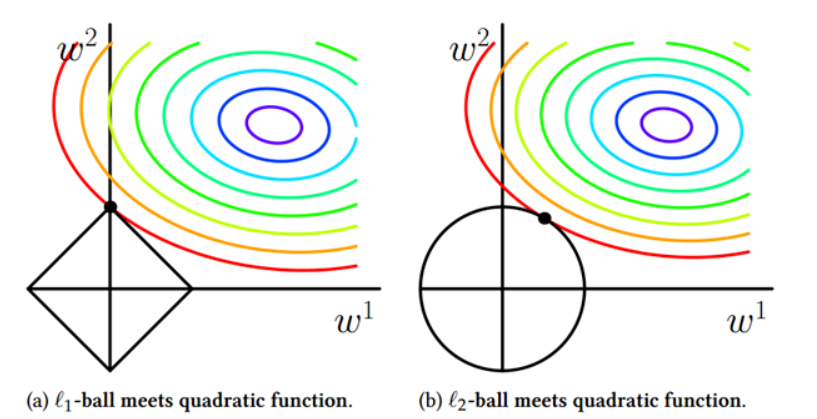
LASSO-线性回归的L1正则
Least Absolute Shrinkage and Selection Operator(LASSO)
Lasso算法(最小绝对值收敛和选择算子、套索算法)是一种同时进行特征选择和正则化(数学)的回归分析方法,旨在增强统计模型的预测准确性和可解释性,最初由斯坦福大学统计学教授Robert Tibshirani于1996年基于Leo Breiman的非负参数推断(Nonnegative Garrote, NNG)提出。
【转载自】
稀疏表示(Sparse Representations) - yif25 - 博客园 https://www.cnblogs.com/yifdu25/p/8128028.html
Dictionary Learning(字典学习、稀疏表示以及其他) - Mario-Chao - 博客园 https://www.cnblogs.com/hdu-zsk/p/5954658.html
l1 和l2范数的真实意义 - limingqi - 博客园 https://www.cnblogs.com/limingqi/p/11621879.html
Lasso算法_xgxyxs的博客-CSDN博客 https://blog.csdn.net/xgxyxs/article/details/79436212