[Codeforces-div.1 24D] Broken robots
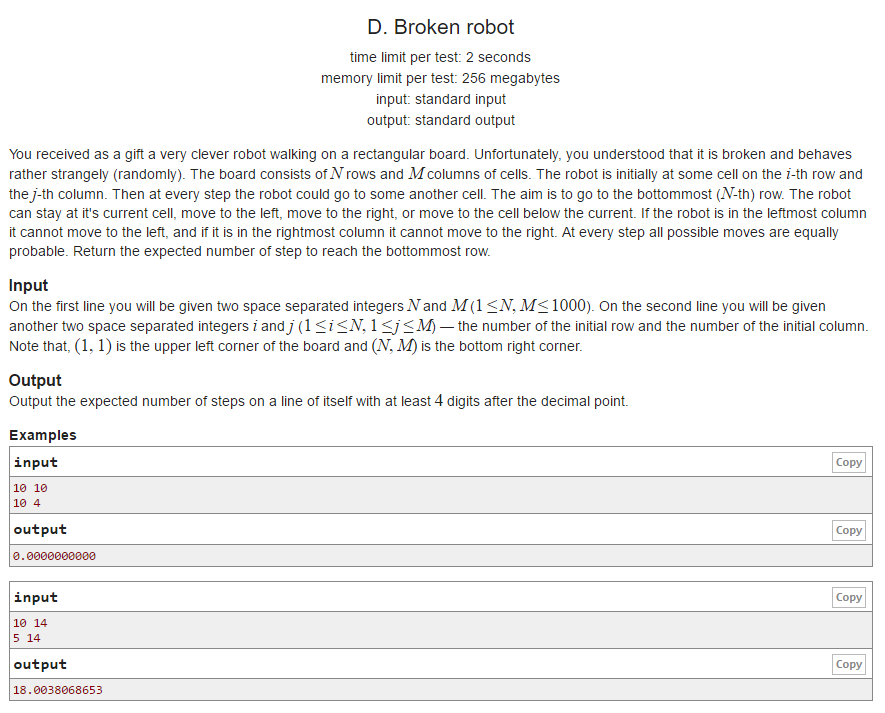
试题分析
显然设(f_{i,j})为到((i,j))的期望步数,将转移表达式列出来。
首先自己跟自己的项消掉。
然后规定一个顺序,设(f_{i+1})已知。
那么(f_i)转移方程中下一行的项就可以直接计算。
然后进行如下手动消元:
- 列出转移方程
- 将上一项带入
- 自己与自己消元
经过这个过程,每一个位置都可以化为(f_{i,j} = f_{i,j+1} imes A+B)的形式。
直接照着方程写就可以了。
#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
#define LL long long
inline int read(){
int x=0,f=1; char c=getchar();
for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
for(;isdigit(c);c=getchar()) x=x*10+c-'0';
return x*f;
}
const int INF = 2147483600;
const int MAXN = 100010;
int N,M; double f[1001][1001];
int X,Y; double A[1001],B[1001];
int main(){
//freopen(".in","r",stdin);
//freopen(".out","w",stdout);
N=read(),M=read(); X=read(),Y=read(); N=N-X+1;
if(M==1){printf("%.10lf
",(N-1)*2.0); return 0;}
for(int i=N-1;i>=1;i--){
A[1]=(3.0+f[i+1][1])/2.0; B[1]=0.5;
for(int j=2;j<M;j++){
A[j]=(4.0+A[j-1]+f[i+1][j])/(3.0-B[j-1]);
B[j]=1.0/(3.0-B[j-1]);
} f[i][M]=(f[i+1][M]+A[M-1]+3.0)/(2.0-B[M-1]);
for(int j=M-1;j>=1;j--){
f[i][j]=f[i][j+1]*B[j]+A[j];
}
} printf("%.10lf
",f[1][Y]);
return 0;
}