【线段树】Mayor's posters

[poj2528]Mayor's posters

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 66154		Accepted: 19104

Description

The citizens of Bytetown, AB, could not stand that the candidates in the mayoral election campaign have been placing their electoral posters at all places at their whim. The city council has finally decided to build an electoral wall for placing the posters and introduce the following rules: 

• Every candidate can place exactly one poster on the wall. 
• All posters are of the same height equal to the height of the wall; the width of a poster can be any integer number of bytes (byte is the unit of length in Bytetown). 
• The wall is divided into segments and the width of each segment is one byte. 
• Each poster must completely cover a contiguous number of wall segments.

They have built a wall 10000000 bytes long (such that there is enough place for all candidates). When the electoral campaign was restarted, the candidates were placing their posters on the wall and their posters differed widely in width. Moreover, the candidates started placing their posters on wall segments already occupied by other posters. Everyone in Bytetown was curious whose posters will be visible (entirely or in part) on the last day before elections. 
Your task is to find the number of visible posters when all the posters are placed given the information about posters' size, their place and order of placement on the electoral wall. 

Input

The first line of input contains a number c giving the number of cases that follow. The first line of data for a single case contains number 1 <= n <= 10000. The subsequent n lines describe the posters in the order in which they were placed. The i-th line among the n lines contains two integer numbers l_i and ri which are the number of the wall segment occupied by the left end and the right end of the i-th poster, respectively. We know that for each 1 <= i <= n, 1 <= l_i <= ri <= 10000000. After the i-th poster is placed, it entirely covers all wall segments numbered l_i, l_i+1 ,... , ri.

Output

For each input data set print the number of visible posters after all the posters are placed. 

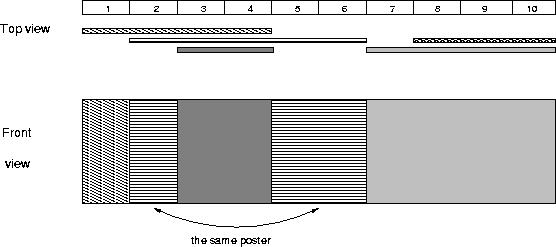
The picture below illustrates the case of the sample input. 

Sample Input

1
5
1 4
2 6
8 10
3 4
7 10

Sample Output

4

Source

Alberta Collegiate Programming Contest 2003.10.18

 

题目大意：T组测试数据，每组测试数据有N张海报，按次序贴在板子上，我们可以将其抽象为一条直线，每张海报占据的区域[L,R]，问最后可以贴几张海报。

试题分析：标记每个区间是否只有一种颜色，如果是的话访问这个区间时看它的颜色编号有没有被算进答案。更新时注意下传标记。

　　　　　  POJ上的数据比较水，建议去试一试discuss中的数据，蛮良心的找出普通离散化的错误……

　　　　　  比如说

1
3
1 3
6 10
1 10

//正确输出：3
//错误输出：2
//问题原因：离散化成了[1,2] [3,4] [1,4]，这样确实只剩下2了

　　　　　　如何解决？在两两之差>1时(区域不会被完全覆盖)，就可以在这里插入一个节点以标记这里有一个区间要算。

代码：

#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
#include<queue>
#include<stack>
#include<algorithm>
using namespace std;

inline int read(){
	int x=0,f=1;char c=getchar();
	for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
	for(;isdigit(c);c=getchar()) x=x*10+c-'0';
	return x*f;
}
const int MAXN=200001;
const int INF=999999;
int N,M;
int T;
int A[MAXN*2],a[MAXN*2],b[MAXN*2];
int tr[MAXN*8+100];
int cnt,tmp3;
bool flag[MAXN*8+100];
bool Hash[MAXN*8+100];
int tmp;

void tage_lazy(int rt,int l,int r){
	if(flag[rt]){
		flag[rt*2]=flag[rt*2+1]=true;
		tr[rt*2]=tr[rt*2+1]=tr[rt];
		flag[rt]=false;
	}
	return ;
}
void add(int l,int r,int rt,int L,int R){
	if(L<=l&&R>=r){
		tr[rt]=cnt;
		flag[rt]=true;
		return ;
	}
	tage_lazy(rt,l,r);
	int mid=(l+r)>>1;
	if(mid<R) add(mid+1,r,rt*2+1,L,R);
	if(mid>=L) add(l,mid,rt*2,L,R);
	return ;
}
int Que(int l,int r,int rt,int L,int R){
	if(flag[rt]){
		if(!Hash[tr[rt]]){
			Hash[tr[rt]]=true;
			return 1;
		}
		else return 0;
	}
	if(l==r) return 0;
	int mid=(l+r)>>1;
	return Que(l,mid,rt*2,L,R)+Que(mid+1,r,rt*2+1,L,R);
}

int main(){
    T=read();
    while(T--){
	    memset(tr,0,sizeof(tr));
	    memset(flag,false,sizeof(flag));
	    memset(Hash,false,sizeof(Hash));
    	N=read();tmp=tmp3=0;
    	for(int i=1;i<=N;i++){
    		++tmp;A[tmp]=a[tmp]=read();
    		++tmp;A[tmp]=a[tmp]=read();
		}
		sort(a+1,a+tmp+1);
		int tmp2=0;int treef=tmp;
		for(int i=1;i<=tmp;i++) 
		    if(a[i]==a[i-1]) treef--;
		    else b[++tmp3]=a[i];
		int k=tmp3;
		for(int i=1;i<=k;i++)
		    if(b[i]>b[i-1]+1) b[++tmp3]=b[i-1]+1;
		sort(b+1,b+tmp3+1);
		treef=tmp3;
		for(int i=1;i<=N;i++){
			++cnt;
			int l=lower_bound(b+1,b+tmp3+1,A[tmp2+1])-b;
			int r=lower_bound(b+1,b+tmp3+1,A[tmp2+2])-b;
			add(1,treef,1,l,r);
			tmp2+=2;
		}
		printf("%d
",Que(1,treef,1,1,treef)); 
	}
}