最长公共子序列:
给定一个序列X={x1,x2,x3...xm},另一个序列Z={z1,z2,z3...zk}满足如下条件时称为X的子序列,即存在一个严格递增的X的下标序列<i1,i2...ik>对所有j=1,2...k满足xi=zj。给定两个序列X,Y,如果既是X的子序列又是Y的子序列,那就称为X,Y的公共子序列。最长公共子序列就是所有子序列中最长的一个或几个。
用动态规划法来解最长公共子序列问题:
1.刻画最长公共子序列的特征
令X={x1,x2,x3...xm},Y={y1,y2,y3...yn},Z={z1,z2,z3...zk}是X,Y的公共子序列。
LCS的最优子结构为:
1.if xm==yn 则zk==xm==yn且zk-1是xm-1,yn-1的LCS
2. if xm != yn 那么zk!=xm意味着Z是xm-1和Y的LCS
3.if xm != yn 那么zk!=yn意味着Z是X和yn-1的LCS
2.递归解
定义c[i][j表示Xi和YjLCS长度,有如下公式:
0 i==0 || j==0
c[i][j] = c[i-1][j-1]+1 i,j>0&&xi==yj
max(c[i][j-1], c[i-1][j]) i,j>0&&xi!=yj
3.计算LCS长度
用b[i][j]来保存子问题的最优解
伪码:(算法导论)
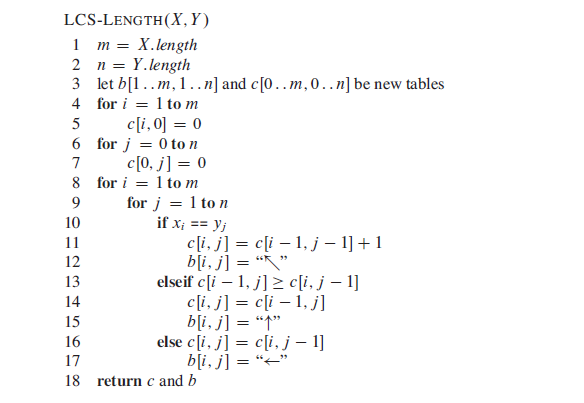
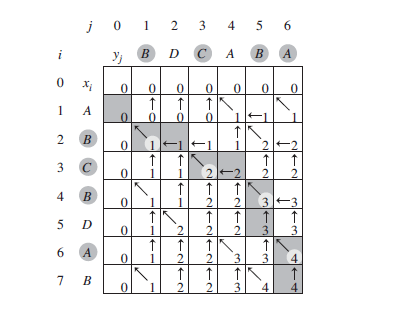
c[i][j]和吧b[i][j]的跟踪
4.构造LCS
伪码:

实现代码:
package dp_lcs; /** *最长公共子序列 *@author wxisme *@time 2015-10-22 下午4:49:44 */ public class Solve_LCS { public static char[] x; public static char[] y; public static int[][] c; //c[i][j]表示xi,yj的lcs public static int[][] b; //记录最优值 /** * 计算LCS */ public static void lcs_length() { int m = x.length+1; int n = y.length+1; c = new int[m][n]; b = new int[m][n]; for(int i=0; i<m; i++) c[i][0] = 0; for(int j=0; j<n; j++) c[0][j] = 0; for(int i=1; i<m; i++) { for(int j=1; j<n; j++) { if(x[i-1] == y[j-1]) { c[i][j] = c[i-1][j-1] + 1; b[i][j] = 1; //左上 } else if(c[i-1][j] >= c[i][j-1]) { c[i][j] = c[i-1][j]; b[i][j] = 2; //上 } else { c[i][j] = c[i][j-1]; b[i][j] = 3; //左 } } } } /** * 构造LCS * @param i * @param j */ public static void print_LCS(int i, int j) { if(i==0 || j==0) return ; if(b[i][j] == 1) { print_LCS(i-1, j-1); System.out.print(x[i-1]); } else if(b[i][j] == 2) { print_LCS(i-1, j); } else { print_LCS(i, j-1); } } }
测试数据:
public static void main(String[] args) { Solve_LCS ret = new Solve_LCS(); x = new char[]{'A', 'B', 'C', 'B', 'D', 'A', 'B'}; y = new char[]{'B', 'D', 'C', 'A', 'B', 'A'}; ret.lcs_length(); ret.print_LCS(x.length, y.length); }
结果:
BCBA
参考算法导论第三版