最长公共子序列

【问题】

若给定序列X={x1,x2,…,xm}，则另一序列Z={z1,z2,…,zk}，是X的子序列是指存在一个严格递增下标序列{i1,i2,…,ik}使得对于所有j=1,2,…,k有：zj=xij。
例如，序列Z={B，C，D，B}是序列X={A，B，C，B，D，A，B}的子序列，相应的递增下标序列为{2，3，5，7}。
给定2个序列X和Y，当另一序列Z既是X的子序列又是Y的子序列时，称Z是序列X和Y的公共子序列。
给定2个序列X={x1,x2,…,xm}和Y={y1,y2,…,yn}，找出X和Y的最长公共子序列（Lonest-Common-Subsequence，LCS）。

【算法分析】

由最长公共子序列问题的最优子结构性质建立子问题最优值的递归关系。
用c[i][j]记录序列和的最长公共子序列的长度。其中， Xi={x1,x2,…,xi}；Yj={y1,y2,…,yj}。
当i=0或j=0时，空序列是Xi和Yj的最长公共子序列。故此时c[i][j]=0。
其他情况下，由最优子结构性质可建立递归关系如下：

 

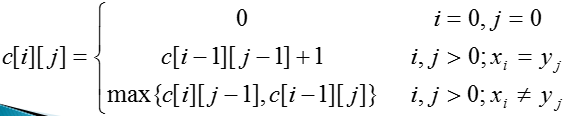
【源代码】

//计算最优值
void LCSLength(int m,int n,char *y,char *x,int **c,int **b)
{    

　　int i, j;
　　for(i=1;i<=m;i++) c[i][0]=0;
　　for(j=0;j<=n;j++) c[0][j]=0;
　　for(i=1;i<=m;i++)
　　　　for(j=1;j<=n;j++)
　　　　{
　　　　　　if (x[i]==y[j])
　　　　　　　　{c[i][j]=c[i-1][j-1]+1; b[i][j]=1;}
　　　　　　else if(c[i-1][j]>=c[i][j-1])
        　　　　{c[i][j]=c[i-1][j]; b[i][j]=2;}
　　　　　　else {c[i][j]=c[i][j-1]; b[i][j]=3;}
　　　　}
}

//构造最长公共子序列
void LCS(int i,int j,char *x,int**b)
{
    if(i==0||j==0)return;
    if(b[i][j]==1){ LCS(i-1,j-1,x,b); cout<<x[i];}
    else if(b[i][j]==2) LCS(i-1,j,x,b);
    else LCS(i,j-1,x,b);
}

【复杂度分析】