相信使用Halcon做过运动目标分析的朋友对create_bg_esti这个算子一定不陌生。对这样一个基于卡尔曼滤波理论的背景模型也有一定的了解。使用卡尔曼背景模型能够适应慢变的环境,将变化缓慢的像素与变化快的像素分离开来,从而得到前景。这样的好处是能够去除如室外白天光线强度变化的带来的影响,但是存在长时间停留的目标会融为背景、快速规则变化的区域会成为前景(树叶、喷泉)等问题。解决这些问题的方法有很多,这里我重点介绍一种——使用熵图像来抑制快速规则变化的运动目标。
在讲熵图像之前,先向大家简单介绍一下熵的概念:
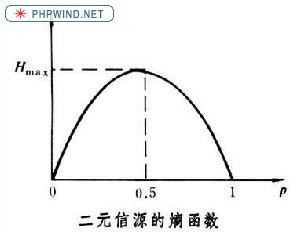
熵,百度百科的定义:熵(entropy)指的是体系的混乱的程度,它在控制论、概率论、数论、天体物理、生命科学等领域都有重要应用,在不同的学科中也有引申出的更为具体的定义,是各领域十分重要的参量。熵由鲁道夫·克劳修斯(RudolfClausius)提出,并应用在热力学中。后来在,克劳德·艾尔伍德·香农(ClaudeElwood Shannon)第一次将熵的概念引入到信息论中来。说简单点就是越混乱熵就越大。
信息熵,是一个数学上的抽象概念,用于衡量信息大小。标准的定义为:
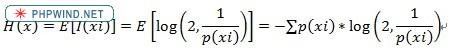
熵图像(entropy_image)。图像中的熵当然是信息熵,每一个像素点都对应一个灰度值。像素灰度值出现得越频繁其包含的信息量也就越小,反之该像素点所携带的信息量就越大。所有像素点的期望值就是这些像素所包含的信息熵H(x)。结果服从如下分布:
在图像中,通常会使用一个矩形的掩膜来进行邻域运算。通过使用3*3、5*5、7*7等等之类矩形的掩膜,对掩膜下的像素点按照求信息熵的公式计算,得到的结果替换掩膜中心位置像素点的值,计算完所有像素点之后得到的图像就是熵图像。效果如下:

在halcon中熵图像的计算使用的算子为entropy_image,该算子计算得到熵之后将结果乘以32来作为最终的值,这样得到的结果就能均匀分布在0~255之间。从图中可以看到,图像中边界、网格等灰度变化快位置的求得的熵值较高,呈现白色,而墙面等变化较小的位置求得的熵值较小,呈现灰色,或者是黑色。利用这样一幅熵图像构造的背景模型就能够很好抑制风吹动树叶这类情况造成的干扰。当然,熵图像本身就对光线变化有一定的抑制。
讲到这里,可能有细心的人会想到,对图像进行平滑也能够实现上述功能。这很正确,没错,不过这仅仅是使用熵图像的一个好处。使用熵图像的另一个好处就是对阴影具有一定的抑制效果。因为被阴影覆盖的区域其亮度衰减厉害,但是熵变化却相对较小,所以只要进行相应的处理是能去除部分阴影的。当然,抑制效果要比专门用于阴影抑制的算法来得弱。
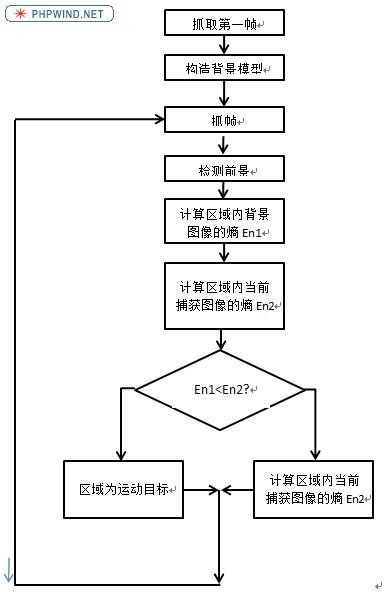
现实生活中运动目标常常会进行长时间的停留,然后再次运动的目标。这种情况下,如果仅仅是使用原图像构造的卡尔曼背景模型来检测运动目标就会在图像中看到两个目标(而实际运动目标只有一个)。针对这种情况,使用熵图像来构造背景模型就能够很好地分辨出哪一个是真正的运动目标。因为在室外,大多数情况下,背景的熵相对人物、车辆都较小,如:操场、柏油路等。通过计算前景区域所覆盖的背景熵图像的均值和前景熵图像的均值就能知道,前景是否是运动目标了。大致方式:
grab_image(Image,AcqHandle)
entropy_image(Image,
ImageEntropy,5, 5)
ImageEntropy,5, 5)
run_bg_esti(ImageEntropy,ForeRegion,
BgEstiHandle)
BgEstiHandle)
give_bg_esti(BackgroundImage,BgEstiHandle)
region_to_mean(ForeRegion,BackgroundImage,
ImageMean1)
ImageMean1)
region_to_mean(ForeRegion,
ImageEntropy,ImageMean2)
ImageEntropy,ImageMean2)
if(ImageMean1>
ImageMean2)
ImageMean2)
区域不是运动目标
else
区域是运动目标
当然,还有更好的使用熵来判断前景区域时进入还是离开的方式。同样是针对路面上的人物、车辆等目标。不过这次构造的背景模型还是直接使用原始图像,且仅仅计算前景区域的熵(entropy_gray)。这种使用方式针对车辆这些大型目标十分有效。算法如下:
人物区域或者车辆目标的熵比较大,使用算子entropy_gray计算出来的结果与地面之间的差异一般都在0.5以上。
熵的公式:
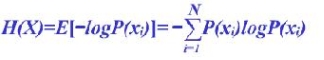
熵图像,图像中的熵当然是信息熵,每一个像素点都对应一个灰度值。像素灰度值出现得越频繁其包含的信息量也就越小,反之该像素点所携带的信息量就越大。所有像素点的期望值就是这些像素所包含的信息熵H(x)

上图所示 图像的熵 a灰度图 b二值图 c灰度图
a c 熵高,是因为 虽然3幅图的像素个数相同,但是灰度值个数不同,b二值图中只有黑色与白色
显然熵低
a c 熵相同说明 熵与像素的位置无关
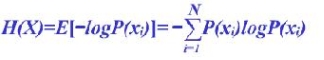
熵图像,图像中的熵当然是信息熵,每一个像素点都对应一个灰度值。像素灰度值出现得越频繁其包含的信息量也就越小,反之该像素点所携带的信息量就越大。所有像素点的期望值就是这些像素所包含的信息熵H(x)

上图所示 图像的熵 a灰度图 b二值图 c灰度图
a c 熵高,是因为 虽然3幅图的像素个数相同,但是灰度值个数不同,b二值图中只有黑色与白色
显然熵低
a c 熵相同说明 熵与像素的位置无关