pytest允许在多个级别启用测试参数化:
- pytest.fixture() 允许fixture有参数化功能(后面讲解)
- @pytest.mark.parametrize 允许在测试函数或类中定义多组参数和fixtures
- pytest_generate_tests 允许定义自定义参数化方案或扩展(拓展)
源码分析
def parametrize(self,argnames, argvalues, indirect=False, ids=None, scope=None):
argnames
源码解析:a comma-separated string denoting one or more argument names, or a list/tuple of argument strings.
含义:参数名字
格式:字符串"arg1,arg2,arg3"【需要用逗号分隔】
备注:源码中写了可以是参数字符串的list或者tuple,但博主实操过是不行的,不知道是不是写的有问题
@pytest.mark.parametrize(["name", "pwd"], [("yy1", "123"), ("yy2", "123")]) # 错的
@pytest.mark.parametrize(("name", "pwd"), [("yy1", "123"), ("yy2", "123")]) # 错的
@pytest.mark.parametrize("name,pwd", [("yy1", "123"), ("yy2", "123")])argvalues
源码解析:
- The list of argvalues determines how often a test is invoked with different argument values.
- If only one argname was specified argvalues is a list of values.【只有一个参数,则是值列表】
- If N argnames were specified, argvalues must be a list of N-tuples, where each tuple-element specifies a value for its respective argname.【如果有多个参数,则用元组来存每一组值】
含义:参数值列表
格式:必须是列表,如:[ val1,val2,val3 ]
如果只有一个参数,里面则是值的列表如:@pytest.mark.parametrize("username", ["yy", "yy2", "yy3"])
如果有多个参数例,则需要用元组来存放值,一个元组对应一组参数的值,如:@pytest.mark.parametrize("name,pwd", [("yy1", "123"), ("yy2", "123"), ("yy3", "123")])
备注:虽然源码说需要list包含tuple,但我试了下,tuple包含list,list包含list也是可以的........
重点
当装饰器 @pytest.mark.parametrize 装饰测试类时,会将数据集合传递给类的所有测试用例方法
“笛卡尔积”,多个参数化装饰器
# 笛卡尔积,组合数据
data_1 = [1, 2, 3]
data_2 = ['a', 'b']
@pytest.mark.parametrize('a', data_1)
@pytest.mark.parametrize('b', data_2)
def test_parametrize_1(a, b):
print(f'笛卡尔积 测试数据为 : {a},{b}')执行结果
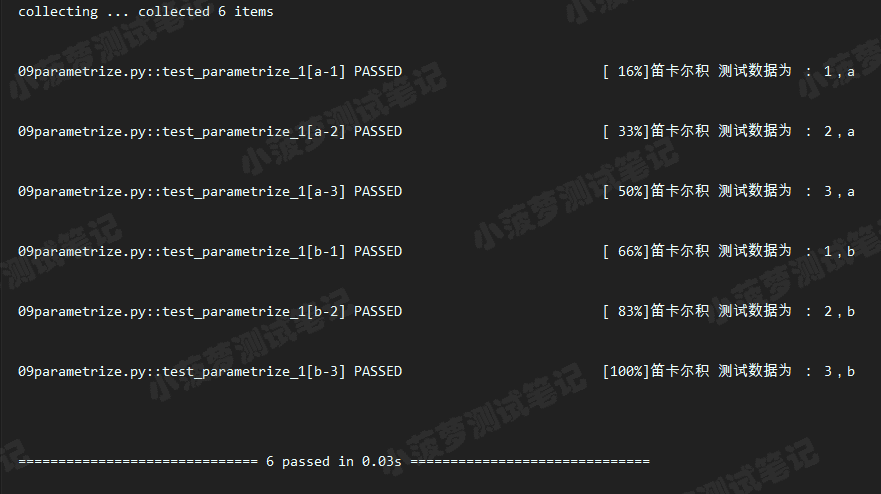
重点知识
- 一个函数或一个类可以装饰多个 @pytest.mark.parametrize
- 这种方式,最终生成的用例数是n*m,比如上面的代码就是:参数a的数据有3个,参数b的数据有2个,所以最终的用例数有3*2=6条
- 当参数化装饰器有很多个的时候,用例数都等于n*n*n*n*....