找出硬币
给你一个装有1 6枚硬币的袋子。1 6枚硬币中有一个是伪造的,并且那个伪造的硬币比真的硬币要轻一些。你的任务是找出这枚伪造的硬币。

金块问题
一袋金块中找最轻and最重的
n≤2,识别出最重和最轻的金块,一次比较就足够了。
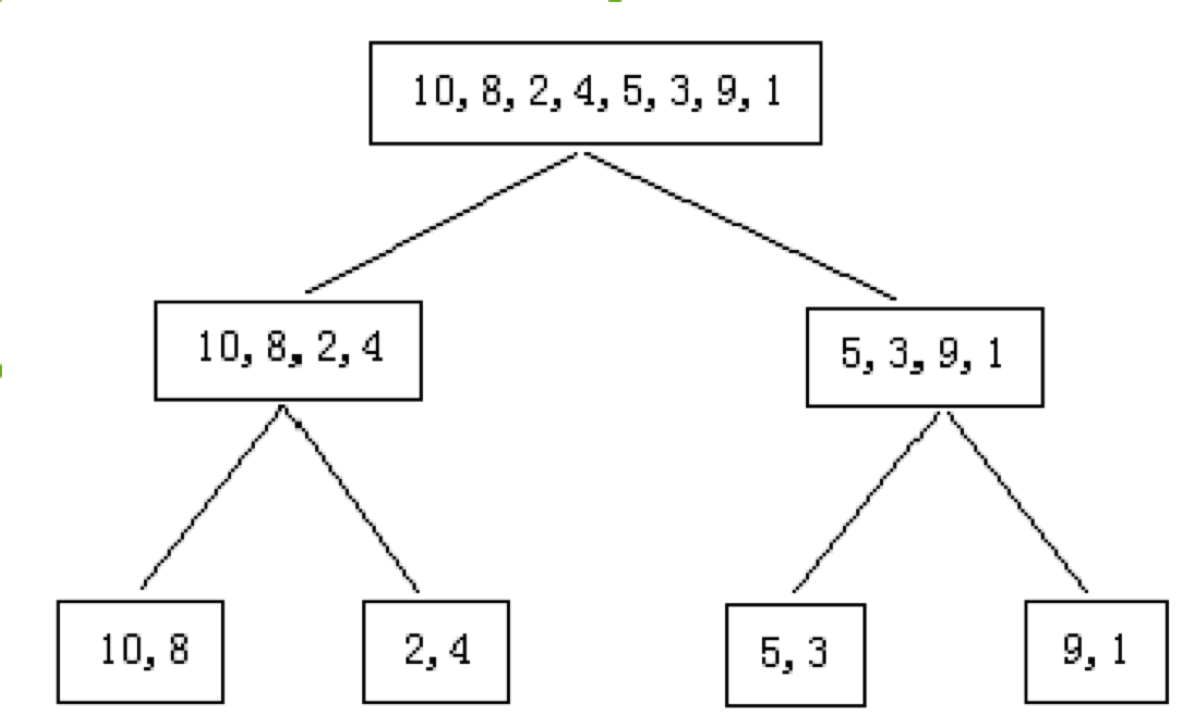
n>2,第一步,把这袋金块平分成两个小袋A和B。第二步,分别找出在A和B中最重和最轻的金块。设A中最重和最轻的金块分别为HA 与LA,以此类推,B中最重和最轻的金块分别为HB 和LB。第三步,通过比较HA 和HB,可以找到所有金块中最重的;通过比较LA 和LB,可以找到所有金块中最轻的。在第二步中,若n>2,则递归地应用分而治之方法。
比较次数:c(n) = 2c(n/2 ) + 2。
分治思想
分治(divide-and-conquer)就是“分而治之”的意思,其实质就是将原问题分成n个规模较小而结构与原问题相似的子问题;然后递归地解这些子问题,最后合并其结果就得到原问题的解。当n=2时的分治法又称二分法。
其三个步骤如下;
分解(Divide):将原问题分成一系列子问题。
解决(Conquer):递归地解各子问题。若子问题足够小,则可直接求解。
合并(combine);将子问题的结果合并成原问题的解。
由分治法所得到的子问题与原问题具有相同的类型。如果得到的子问题相对来说还太大,则可反复使用分治策略将这些子问题分成更小的同类型子问题,直至产生出不用进一步细分就可求解的子问题。
分治求解可用一个递归过程来表示。
要使分治算法效率高,关键在于如何分割?一般地,出于一种平衡原则,总是把大问题分成K个规模尽可能相等的子问题,但也有例外,如求表的最大最小元问题的算法,当n=6时,等分定量成两个规模为3的子表L1和L2不是最佳分割。
分治策略的解题思路
if 问题不可分then begin
直接求解;
返回问题的解;
end
else begin
对原问题进行分治;
递归对每一个分治的部分求解
归并整个问题,得出全问题的解;
end;
一元三次方程求解
有形如:ax3+bx2+cx+d=0这样的一个一元三次方程。给出该方程中各项的系数(a,b,c,d均为实数),并约定该方程存在三个不同实根(根的范围在-100至100之间),且根与根之差的绝对值>=1。要求由小到大依次在同一行输出这三个实根(根与根之间留有空格),并精确到小数点后4位。
提示:记方程f(x)=ax3+bx2+cx+d,若存在2个数x1和x2,且x1<x2,f(x1)*f(x2)<0,则在(x1,x2)之间一定有一个根。
样例
输入:1 -5 -4 20
输出:-2.00 2.00 5.00
A当已知区间(a,b)内有一个根时,用二分法求根,若区间(a,b)内有根,则必有f(a)·f(b)<0。重复执行如下的过程:
(1)若a+0.0001>b或f((a+b)/2)=0,则可确定根为(a+b)/2并退出过程;
(2)若f(a)* f((a+b)/2)<0,则由题目给出的定理可知根在区间(a,(a+b)/2)中,故对区间重复该过程;
(3)若f(a)* f((a+b)/2)>0 ,则必然有f((a+b)/2)* f(b)<0 ,根在((a+b)/2,b)中,对此区间重复该过程。
执行完毕,就可以得到精确到0.0001的根。
B求方程的所有三个实根
所有的根的范围都在-100至100之间,且根与根之差的绝对值>=1。因此可知:在[-100,-99]、[-99,-98]、……、[99,100]、[100,100]这201个区间内,每个区间内至多只能有一个根。即:除区间[100,100]外,其余区间[a,a+1],只有当f(a)=0或f(a)·f(a+1)<0时,方程在此区间内才有解。若f(a)=0 ,解即为a;若f(a)·f(a+1)<0 ,则可以利用A中所述的二分法迅速出找出解。