Leetcode——链表和数组（6）

柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

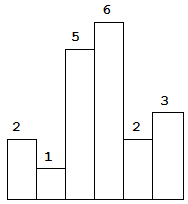
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

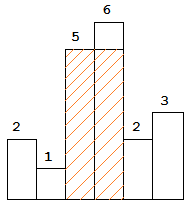
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

示例:

输入: [2,1,5,6,2,3]
输出: 10

暴力+剪枝

遍历数组，每找到一个局部峰值（只要当前的数字大于后面的一个数字，那么当前数字就看作一个局部峰值，跟前面的数字大小无关），

然后向前遍历所有的值，算出共同的矩形面积，每次对比保留最大值。

这里再说下为啥要从局部峰值处理，看题目中的例子，局部峰值为 2，6，3，我们只需在这些局部峰值出进行处理，为啥不用在非局部峰值处统计呢，这是因为非局部峰值处的情况，后面的局部峰值都可以包括，比如1和5，由于局部峰值6是高于1和5的，所有1和5能组成的矩形，到6这里都能组成，并且还可以加上6本身的一部分组成更大的矩形，那么就不用费力气去再统计一个1和5处能组成的矩形了。

// Pruning optimize
class Solution {
public:
    int largestRectangleArea(vector<int> &height) {
        int res = 0;
        for (int i = 0; i < height.size(); ++i) {
            if (i + 1 < height.size() && height[i] <= height[i + 1]) {
                continue;
            }
            int minH = height[i];
            for (int j = i; j >= 0; --j) {
                minH = min(minH, height[j]);
                int area = minH * (i - j + 1);
                res = max(res, area);
            }
        }
        return res;
    }
};

栈

维护一个栈，用来保存递增序列，相当于上面那种方法的找局部峰值。我们可以看到，直方图矩形面积要最大的话，需要尽可能的使得连续的矩形多，并且最低一块的高度要高。有点像木桶原理一样，总是最低的那块板子决定桶的装水量。

那么既然需要用单调栈来做，首先要考虑到底用递增栈，还是用递减栈来做。

递增栈是维护递增的顺序，当遇到小于栈顶元素的数就开始处理，而递减栈正好相反，维护递减的顺序，当遇到大于栈顶元素的数开始处理。

根据这道题的特点，我们需要按从高板子到低板子的顺序处理，先处理最高的板子，宽度为1，然后再处理旁边矮一些的板子，此时长度为2，因为之前的高板子可组成矮板子的矩形 ，因此我们需要一个递增栈，当遇到大的数字直接进栈，而当遇到小于栈顶元素的数字时，就要取出栈顶元素进行处理了，那取出的顺序就是从高板子到矮板子了，于是乎遇到的较小的数字只是一个触发，表示现在需要开始计算矩形面积了，为了使得最后一块板子也被处理，这里用了个小 trick，在高度数组最后面加上一个0，这样原先的最后一个板子也可以被处理了。

由于栈顶元素是矩形的高度，那么关键就是求出来宽度，单调栈中不能放高度，而是需要放坐标。由于我们先取出栈中最高的板子，那么就可以先算出长度为1的矩形面积了，然后再取下一个板子，此时根据矮板子的高度算长度为2的矩形面积，以此类推，知道数字大于栈顶元素为止，再次进栈

class Solution {
public:
    int largestRectangleArea(vector<int> &height) {
        int res = 0;
        stack<int> st;
        height.push_back(0);
        for (int i = 0; i < height.size(); ++i) {
            if (st.empty() || height[st.top()] < height[i]) {
                st.push(i);
            } else {
                int cur = st.top(); st.pop();
                res = max(res, height[cur] * (st.empty() ? i : (i - st.top() - 1)));
                --i;
            }     
        }
        return res;
    }
};

栈 简化

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int res = 0;
        stack<int> st;
        heights.push_back(0);
        for (int i = 0; i < heights.size(); ++i) {
            while (!st.empty() && heights[st.top()] >= heights[i]) {
                int cur = st.top(); st.pop();
                res = max(res, heights[cur] * (st.empty() ? i : (i - st.top() - 1)));
            }
            st.push(i);
        }
        return res;
    }
};

最大矩形

给定一个仅包含 0 和 1 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例:

输入:
[
  ["1","0","1","0","0"],
  ["1","0","1","1","1"],
  ["1","1","1","1","1"],
  ["1","0","0","1","0"]
]
输出: 6

栈

与柱状图中最大的矩形类似，将每一层都当作直方图的底层，并向上构造整个直方图，

由于题目限定了输入矩阵的字符只有 '0' 和 '1' 两种，所以处理起来也相对简单。

方法是，对于每一个点，如果是 ‘0’，则赋0，如果是 ‘1’，就赋之前的 height 值加上1。

class Solution {
public:
    int maximalRectangle(vector<vector<char> > &matrix) {
        int res = 0;
        vector<int> height;
        for (int i = 0; i < matrix.size(); ++i) {
            height.resize(matrix[i].size());
            for (int j = 0; j < matrix[i].size(); ++j) {
                height[j] = matrix[i][j] == '0' ? 0 : (1 + height[j]);
            }
            res = max(res, largestRectangleArea(height));
        }
        return res;
    }
    int largestRectangleArea(vector<int>& height) {
        int res = 0;
        stack<int> s;
        height.push_back(0);
        for (int i = 0; i < height.size(); ++i) {
            if (s.empty() || height[s.top()] <= height[i]) s.push(i);
            else {
                int tmp = s.top(); s.pop();
                res = max(res, height[tmp] * (s.empty() ? i : (i - s.top() - 1)));
                --i;
            }
        }
        return res;
    }
};

方法二

left 数组表示若当前位置是1且与其相连都是1的左边界的位置（若当前 height 是0，则当前 left 一定是0），

right 数组表示若当前位置是1且与其相连都是1的右边界的位置再加1（加1是为了计算长度方便，直接减去左边界位置就是长度），初始化为n（若当前 height 是0，则当前 right 一定是n），那么对于任意一行的第j个位置，矩形为 (right[j] - left[j]) * height[j]，我们举个例子来说明，比如给定矩阵为：

[
  [1, 1, 0, 0, 1],
  [0, 1, 0, 0, 1],
  [0, 0, 1, 1, 1],
  [0, 0, 1, 1, 1],
  [0, 0, 0, 0, 1]
]

第0行：

h: 1 1 0 0 1
l: 0 0 0 0 4
r: 2 2 5 5 5 

第1行：

h: 0 2 0 0 2
l: 0 1 0 0 4
r: 5 2 5 5 5 

第2行：

h: 0 0 1 1 3
l: 0 0 2 2 4
r: 5 5 5 5 5

第3行：

h: 0 0 2 2 4
l: 0 0 2 2 4
r: 5 5 5 5 5

第4行：

h: 0 0 0 0 5
l: 0 0 0 0 4
r: 5 5 5 5 5 

class Solution {
public:
    int maximalRectangle(vector<vector<char>>& matrix) {
        if (matrix.empty() || matrix[0].empty()) return 0;
        int res = 0, m = matrix.size(), n = matrix[0].size();
        vector<int> height(n, 0), left(n, 0), right(n, n);
        for (int i = 0; i < m; ++i) {
            int cur_left = 0, cur_right = n;
            for (int j = 0; j < n; ++j) {
                if (matrix[i][j] == '1') {
                    ++height[j];
                    left[j] = max(left[j], cur_left);
                } else {
                    height[j] = 0;
                    left[j] = 0;
                    cur_left = j + 1;
                }
            }
            for (int j = n - 1; j >= 0; --j) {
                if (matrix[i][j] == '1') {
                    right[j] = min(right[j], cur_right);
                } else {
                    right[j] = n;
                    cur_right = j;
                }
                res = max(res, (right[j] - left[j]) * height[j]);
            }
        }
        return res;
    }
};

统计

统计每一行的连续1的个数，使用一个数组 h_max, 其中 h_max[i][j] 表示第i行，第j个位置水平方向连续1的个数，若 matrix[i][j] 为0，那对应的 h_max[i][j] 也一定为0。

统计的过程跟建立累加和数组很类似，唯一不同的是遇到0了要将 h_max 置0。这个统计好了之后，只需要再次遍历每个位置，首先每个位置的 h_max 值都先用来更新结果 res，因为高度为1也可以看作是矩形，然后我们向上方遍历，上方 (i, j-1) 位置也会有 h_max 值，但是用二者之间的较小值才能构成矩形，用新的矩形面积来更新结果 res，这样一直向上遍历，直到遇到0，或者是越界的时候停止，这样就可以找出所有的矩形了

class Solution {
public:
    int maximalRectangle(vector<vector<char>>& matrix) {
        if (matrix.empty() || matrix[0].empty()) return 0;
        int res = 0, m = matrix.size(), n = matrix[0].size();
        vector<vector<int>> h_max(m, vector<int>(n));
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (matrix[i][j] == '0') continue;
                if (j > 0) h_max[i][j] = h_max[i][j - 1] + 1;
                else h_max[i][0] = 1;
            }
        }
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (h_max[i][j] == 0) continue;
                int mn = h_max[i][j];
                res = max(res, mn);
                for (int k = i - 1; k >= 0 && h_max[k][j] != 0; --k) {
                    mn = min(mn, h_max[k][j]);
                    res = max(res, mn * (i - k + 1));
                }
            }
        }
        return res;
    }
};

最大正方形

在一个由 0 和 1 组成的二维矩阵内，找到只包含 1 的最大正方形，并返回其面积。

示例:

输入: 

1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0

输出: 4

暴力

把数组中每一个点都当成正方形的左顶点来向右下方扫描，来寻找最大正方形。具体的扫描方法是，确定了左顶点后，再往下扫的时候，正方形的竖边长度就确定了，只需要找到横边即可，这时候我们使用直方图的原理，从其累加值能反映出上面的值是否全为1。

class Solution {
public:
    int maximalSquare(vector<vector<char> >& matrix) {
        int res = 0;
        for (int i = 0; i < matrix.size(); ++i) {
            vector<int> v(matrix[i].size(), 0);
            for (int j = i; j < matrix.size(); ++j) {
                for (int k = 0; k < matrix[j].size(); ++k) {
                    if (matrix[j][k] == '1') ++v[k];
                }
                res = max(res, getSquareArea(v, j - i + 1));
            }
        }
        return res;
    }
    int getSquareArea(vector<int> &v, int k) {
        if (v.size() < k) return 0;
        int count = 0;
        for (int i = 0; i < v.size(); ++i) {
            if (v[i] != k) count = 0; 
            else ++count;
            if (count == k) return k * k;
        }
        return 0;
    }
};

建立累计和数组

原理是建立好了累加和数组后，我们开始遍历二维数组的每一个位置，对于任意一个位置 (i, j)，我们从该位置往 (0,0) 点遍历所有的正方形，正方形的个数为 min(i,j)+1，由于我们有了累加和矩阵，能快速的求出任意一个区域之和，所以我们能快速得到所有子正方形之和，比较正方形之和跟边长的平方是否相等，相等说明正方形中的数字均为1，更新 res 结果即可，参见代码如下：

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        if (matrix.empty() || matrix[0].empty()) return 0;
        int m = matrix.size(), n = matrix[0].size(), res = 0;
        vector<vector<int>> sum(m, vector<int>(n, 0));
        for (int i = 0; i < matrix.size(); ++i) {
            for (int j = 0; j < matrix[i].size(); ++j) {
                int t = matrix[i][j] - '0';
                if (i > 0) t += sum[i - 1][j];
                if (j > 0) t += sum[i][j - 1];
                if (i > 0 && j > 0) t -= sum[i - 1][j - 1];
                sum[i][j] = t;
                int cnt = 1;
                for (int k = min(i, j); k >= 0; --k) {
                    int d = sum[i][j];
                    if (i - cnt >= 0) d -= sum[i - cnt][j];
                    if (j - cnt >= 0) d -= sum[i][j - cnt];
                    if (i - cnt >= 0 && j - cnt >= 0) d += sum[i - cnt][j - cnt];
                    if (d == cnt * cnt) res = max(res, d);
                    ++cnt;
                }
            }
        }
        return res;
    }
};

二维动态规划

我们还可以进一步的优化时间复杂度到 O(n2)，做法是使用 DP，建立一个二维 dp 数组，其中 dp[i][j] 表示到达 (i, j) 位置所能组成的最大正方形的边长。

我们首先来考虑边界情况，也就是当i或j为0的情况，那么在首行或者首列中，必定有一个方向长度为1，那么就无法组成长度超过1的正方形，最多能组成长度为1的正方形，条件是当前位置为1。

边界条件处理完了，再来看一般情况的递推公式怎么办，对于任意一点 dp[i][j]，由于该点是正方形的右下角，所以该点的右边，下边，右下边都不用考虑，关心的就是左边，上边，和左上边。

这三个位置的dp值 suppose 都应该算好的，还有就是要知道一点，只有当前 (i, j) 位置为1，dp[i][j] 才有可能大于0，否则 dp[i][j] 一定为0。

当 (i, j) 位置为1，此时要看 dp[i-1][j-1], dp[i][j-1]，和 dp[i-1][j] 这三个位置，我们找其中最小的值，并加上1，就是 dp[i][j] 的当前值了，这个并不难想，毕竟不能有0存在，所以只能取交集，最后再用 dp[i][j] 的值来更新结果 res 的值即可

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        if (matrix.empty() || matrix[0].empty()) return 0;
        int m = matrix.size(), n = matrix[0].size(), res = 0;
        vector<vector<int>> dp(m, vector<int>(n, 0));
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i == 0 || j == 0) dp[i][j] = matrix[i][j] - '0';
                else if (matrix[i][j] == '1') {
                    dp[i][j] = min(dp[i - 1][j - 1], min(dp[i][j - 1], dp[i - 1][j])) + 1;
                }
                res = max(res, dp[i][j]);
            }
        }
        return res * res;
    }
};

一维动态规划

为了处理边界情况，padding 了一位，所以 dp 的长度是 m+1，然后还需要一个变量 pre 来记录上一个层的 dp 值，我们更新的顺序是行优先，就是先往下遍历，用一个临时变量t保存当前 dp 值，然后看如果当前位置为1，则更新 dp[i] 为 dp[i], dp[i-1], 和 pre 三者之间的最小值，再加上1，来更新结果 res，如果当前位置为0，则重置当前 dp 值为0，因为只有一维数组，每个位置会被重复使用

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        if (matrix.empty() || matrix[0].empty()) return 0;
        int m = matrix.size(), n = matrix[0].size(), res = 0, pre = 0;
        vector<int> dp(m + 1, 0);
        for (int j = 0; j < n; ++j) {
            for (int i = 1; i <= m; ++i) {
                int t = dp[i];
                if (matrix[i - 1][j] == '1') {
                    dp[i] = min(dp[i], min(dp[i - 1], pre)) + 1;
                    res = max(res, dp[i]);
                } else {
                    dp[i] = 0;
                }
                pre = t;
            }
        }
        return res * res;
    }
};

最长连续序列

给定一个未排序的整数数组，找出最长连续序列的长度。

要求算法的时间复杂度为 O(n)。

示例:

输入: [100, 4, 200, 1, 3, 2]
输出: 4
解释: 最长连续序列是 [1, 2, 3, 4]。它的长度为 4。

HashSet

使用一个集合HashSet存入所有的数字，然后遍历数组中的每个数字，如果其在集合中存在，那么将其移除，然后分别用两个变量pre和next算出其前一个数跟后一个数，然后在集合中循环查找，如果pre在集合中，那么将pre移除集合，然后pre再自减1，直至pre不在集合之中，对next采用同样的方法，那么next-pre-1就是当前数字的最长连续序列，更新res即可。

这里再说下，为啥当检测某数字在集合中存在当时候，都要移除数字。这是为了避免大量的重复计算，就拿题目中的例子来说吧，我们在遍历到4的时候，会向下遍历3，2，1，如果都不移除数字的话，遍历到1的时候，还会遍历2，3，4。

同样，遍历到3的时候，向上遍历4，向下遍历2，1，等等等。如果数组中有大量的连续数字的话，那么就有大量的重复计算，十分的不高效，所以我们要从HashSet中移除数字，代码如下：

class Solution {
public:
    int longestConsecutive(vector<int>& nums) {
        int res = 0;
        unordered_set<int> s(nums.begin(), nums.end());
        for (int val : nums) {
            if (!s.count(val)) continue;
            s.erase(val);
            int pre = val - 1, next = val + 1;
            while (s.count(pre)) s.erase(pre--);
            while (s.count(next)) s.erase(next++);
            res = max(res, next - pre - 1);
        }
        return res;
    }
};

哈希

我们也可以采用哈希表来做，刚开始HashMap为空，然后遍历所有数字，如果该数字不在HashMap中，那么我们分别看其左右两个数字是否在HashMap中，

如果在，则返回其哈希表中映射值，

若不在，则返回0，虽然我们直接从HashMap中取不存在的映射值，也能取到0，但是一旦去取了，就会自动生成一个为0的映射，那么我们这里再for循环的开头判断如果存在映射就跳过的话，就会出错。

然后我们将left+right+1作为当前数字的映射，并更新res结果，同时更新num-left和num-right的映射值。

下面来解释一下为啥要判断如何存在映射的时候要跳过，这是因为一旦某个数字创建映射了，说明该数字已经被处理过了，那么其周围的数字很可能也已经建立好了映射了，

如果再遇到之前处理过的数字，再取相邻数字的映射值累加的话，会出错。

举个例子，比如数组 [1, 2, 0, 1]，当0执行完以后，HashMap中的映射为 {1->2, 2->3, 0->3}，可以看出此时0和2的映射值都已经为3了，那么如果最后一个1还按照原来的方法处理，随后得到结果就是7，明显不合题意。

之前说的，为了避免访问不存在的映射值时，自动创建映射，我们使用m.count() 先来检测一下，只有存在映射，我们才从中取值，否则就直接赋值为0

class Solution {
public:
    int longestConsecutive(vector<int>& nums) {
        int res = 0;
        unordered_map<int, int> m;
        for (int num : nums) {
            if (m.count(num)) continue;
            int left = m.count(num - 1) ? m[num - 1] : 0;
            int right = m.count(num + 1) ? m[num + 1] : 0;
            int sum = left + right + 1;
            m[num] = sum;
            res = max(res, sum);
            m[num - left] = sum;
            m[num + right] = sum;
        }
        return res;
    }
};

除自身以外数组的乘积

给你一个长度为 n 的整数数组 nums，其中 n > 1，返回输出数组 output ，其中 output[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积。

示例:

输入: [1,2,3,4]
输出: [24,12,8,6]

提示：题目数据保证数组之中任意元素的全部前缀元素和后缀（甚至是整个数组）的乘积都在 32 位整数范围内。

说明: 请不要使用除法，且在 O(n) 时间复杂度内完成此题。

进阶：
你可以在常数空间复杂度内完成这个题目吗？（ 出于对空间复杂度分析的目的，输出数组不被视为额外空间。）

双向遍历

分别创建出这两个数组即可，分别从数组的两个方向遍历就可以分别创建出乘积累积数组。

class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
        int n = nums.size();
        vector<int> fwd(n, 1), bwd(n, 1), res(n);
        for (int i = 0; i < n - 1; ++i) {
            fwd[i + 1] = fwd[i] * nums[i];
        }
        for (int i = n - 1; i > 0; --i) {
            bwd[i - 1] = bwd[i] * nums[i];
        }
        for (int i = 0; i < n; ++i) {
            res[i] = fwd[i] * bwd[i];
        }
        return res;
    }
};

优化

我们可以对上面的方法进行空间上的优化，由于最终的结果都是要乘到结果 res 中，所以可以不用单独的数组来保存乘积，而是直接累积到结果 res 中，

我们先从前面遍历一遍，将乘积的累积存入结果 res 中，然后从后面开始遍历，用到一个临时变量 right，初始化为1，然后每次不断累积，最终得到正确结果

class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
        vector<int> res(nums.size(), 1);
        for (int i = 1; i < nums.size(); ++i) {
            res[i] = res[i - 1] * nums[i - 1];
        }
        int right = 1;
        for (int i = nums.size() - 1; i >= 0; --i) {
            res[i] *= right;
            right *= nums[i];
        }
        return res;
    }
};

任务调度器

给定一个用字符数组表示的 CPU 需要执行的任务列表。其中包含使用大写的 A - Z 字母表示的26 种不同种类的任务。任务可以以任意顺序执行，并且每个任务都可以在 1 个单位时间内执行完。CPU 在任何一个单位时间内都可以执行一个任务，或者在待命状态。

然而，两个相同种类的任务之间必须有长度为 n 的冷却时间，因此至少有连续 n 个单位时间内 CPU 在执行不同的任务，或者在待命状态。

你需要计算完成所有任务所需要的最短时间。

示例 ：

输入：tasks = ["A","A","A","B","B","B"], n = 2
输出：8
解释：A -> B -> (待命) -> A -> B -> (待命) -> A -> B.
     在本示例中，两个相同类型任务之间必须间隔长度为 n = 2 的冷却时间，而执行一个任务只需要一个单位时间，所以中间出现了（待命）状态。 

提示：

1. 任务的总个数为 [1, 10000]。
2. n 的取值范围为 [0, 100]。

方法一

由于题目中规定了两个相同任务之间至少隔n个时间点，那么我们首先应该处理的出现次数最多的那个任务，先确定好这些高频任务，然后再来安排那些低频任务。

如果任务F的出现频率最高，为k次，那么我们用n个空位将每两个F分隔开，然后我们按顺序加入其他低频的任务，来看一个例子：

AAAABBBEEFFGG 3

我们发现任务A出现了4次，频率最高，于是我们在每个A中间加入三个空位，如下：

A---A---A---A

AB--AB--AB--A  (加入B)

ABE-ABE-AB--A  (加入E)

ABEFABE-ABF-A  (加入F，每次尽可能填满或者是均匀填充)

ABEFABEGABFGA  (加入G)

再来看一个例子：

ACCCEEE 2

我们发现任务C和E都出现了三次，那么我们就将CE看作一个整体，在中间加入一个位置即可：

CE-CE-CE

CEACE-CE  (加入A)

注意最后面那个idle不能省略，不然就不满足相同两个任务之间要隔2个时间点了。

这道题好在没有让我们输出任务安排结果，而只是问所需的时间总长，那么我们就想个方法来快速计算出所需时间总长即可。

我们仔细观察上面两个例子可以发现，都分成了(mx - 1)块，再加上最后面的字母，其中mx为最大出现次数。

比如例子1中，A出现了4次，所以有A---模块出现了3次，再加上最后的A，每个模块的长度为4。

例子2中，CE-出现了2次，再加上最后的CE，每个模块长度为3。

我们可以发现，模块的次数为任务最大次数减1，模块的长度为n+1，最后加上的字母个数为出现次数最多的任务，可能有多个并列。

这样三个部分都搞清楚了，写起来就不难了，我们统计每个大写字母出现的次数，然后排序，这样出现次数最多的字母就到了末尾，然后我们向前遍历，找出出现次数一样多的任务个数，就可以迅速求出总时间长了，下面这段代码可能最不好理解的可能就是最后一句了，那么我们特别来讲解一下。

先看括号中的第二部分，前面分析说了mx是出现的最大次数，mx-1是可以分为的块数，n+1是每块中的个数，而后面的 25-i 是还需要补全的个数，用之前的例子来说明：

AAAABBBEEFFGG 3

A出现了4次，最多，mx=4，那么可以分为mx-1=3块，如下：

A---A---A---

每块有n+1=4个，最后还要加上末尾的一个A，也就是25-24=1个任务，最终结果为13：

ABEFABEGABFGA

再来看另一个例子：

ACCCEEE 2

C和E都出现了3次，最多，mx=3，那么可以分为mx-1=2块，如下：

CE-CE-

每块有n+1=3个，最后还要加上末尾的一个CE，也就是25-23=2个任务，最终结果为8：

CEACE-CE

好，那么此时你可能会有疑问，为啥还要跟原任务个数len相比，取较大值呢？我们再来看一个例子：

AAABBB 0

A和B都出现了3次，最多，mx=3，那么可以分为mx-1=2块，如下：

ABAB

每块有n+1=1个？你会发现有问题，这里明明每块有两个啊，为啥这里算出来n+1=1呢，因为给的n=0，这有没有矛盾呢，没有！因为n表示相同的任务间需要间隔的个数，那么既然这里为0了，说明相同的任务可以放在一起，这里就没有任何限制了，我们只需要执行完所有的任务就可以了，所以我们最终的返回结果一定不能小于任务的总个数len的，这就是要对比取较大值的原因了。

class Solution {
public:
    int leastInterval(vector<char>& tasks, int n) {
        vector<int> cnt(26, 0);
        for (char task : tasks) {
            ++cnt[task - 'A'];
        }
        sort(cnt.begin(), cnt.end());
        int i = 25, mx = cnt[25], len = tasks.size();
        while (i >= 0 && cnt[i] == mx) --i;
        return max(len, (mx - 1) * (n + 1) + 25 - i);
    }
};

方法二

先算出所有空出来的位置，然后计算出所有需要填入的task的个数，如果超出了空位的个数，就需要最后再补上相应的个数。

注意这里如果有多个任务出现次数相同，

那么将其整体放一起，就像上面的第二个例子中的CE一样，那么此时每个part中的空位个数就是n - (mxCnt - 1)，

那么空位的总数就是part的总数乘以每个part中空位的个数了，

那么我们此时除去已经放入part中的，还剩下的task的个数就是task的总个数减去mx * mxCnt，

然后此时和之前求出的空位数相比较，如果空位数要大于剩余的task数，那么则说明还需补充多余的空位，否则就直接返回task的总数即可

class Solution {
public:
    int leastInterval(vector<char>& tasks, int n) {
        int mx = 0, mxCnt = 0;
        vector<int> cnt(26, 0);        
        for (char task : tasks) {
            ++cnt[task - 'A'];
            if (mx == cnt[task - 'A']) {
                ++mxCnt;
            } else if (mx < cnt[task - 'A']) {
                mx = cnt[task - 'A'];
                mxCnt = 1;
            }
        }
        int partCnt = mx - 1;
        int partLen = n - (mxCnt - 1);
        int emptySlots = partCnt * partLen;
        int taskLeft = tasks.size() - mx * mxCnt;
        int idles = max(0, emptySlots - taskLeft);
        return tasks.size() + idles;
    }
};

方法三

建立一个优先队列，然后把统计好的个数都存入优先队列中，那么大的次数会在队列的前面。

这题还是要分块，每块能装n+1个任务，装任务是从优先队列中取，每个任务取一个，装到一个临时数组中，然后遍历取出的任务，

对于每个任务，将其哈希表映射的次数减1，如果减1后，次数仍大于0，则将此任务次数再次排入队列中，遍历完后如果队列不为空，说明该块全部被填满，则结果加上n+1。

我们之前在队列中取任务是用个变量cnt来记录取出任务的个数，我们想取出n+1个，如果队列中任务数少于n+1个，那就用cnt来记录真实取出的个数，当队列为空时，就加上cnt的个数，参见代码如下：

class Solution {
public:
    int leastInterval(vector<char>& tasks, int n) {
        int res = 0, cycle = n + 1;
        unordered_map<char, int> m;
        priority_queue<int> q;
        for (char c : tasks) ++m[c];
        for (auto a : m) q.push(a.second);
        while (!q.empty()) {
            int cnt = 0;
            vector<int> t;
            for (int i = 0; i < cycle; ++i) {
                if (!q.empty()) {
                    t.push_back(q.top()); q.pop();
                    ++cnt;
                }
            }
            for (int d : t) {
                if (--d > 0) q.push(d);
            }
            res += q.empty() ? cnt : cycle;
        }
        return res;
    }
};

重构字符串

给定一个字符串S，检查是否能重新排布其中的字母，使得两相邻的字符不同。

若可行，输出任意可行的结果。若不可行，返回空字符串。

示例 1:

输入: S = "aab"
输出: "aba"

示例 2:

输入: S = "aaab"
输出: ""

注意:

• S 只包含小写字母并且长度在[1, 500]区间内。

哈希

统计每个字符串出现的次数啊，这里使用 HashMap 来建立字母和其出现次数之间的映射。

由于希望次数多的字符排前面，可以使用一个最大堆，C++ 中就是优先队列 Priority Queue，将次数当做排序的 key，把次数和其对应的字母组成一个 pair，放进最大堆中自动排序。

这里其实有个剪枝的 trick，如果某个字母出现的频率大于总长度的一半了，那么必然会有两个相邻的字母出现。

所以在将映射对加入优先队列时，先判断下次数，超过总长度一半了的话直接返回空串就行了。

每次从优先队列中取队首的两个映射对儿处理，因为要拆开相同的字母，这两个映射对儿肯定是不同的字母，可以将其放在一起，之后需要将两个映射对儿中的次数自减1，如果还有多余的字母，即减1后的次数仍大于0的话，将其再放回最大堆。

由于是两个两个取的，所以最后 while 循环退出后，有可能优先队列中还剩下了一个映射对儿，此时将其加入结果 res 即可。而且这个多余的映射对儿一定只有一个字母了，因为提前判断过各个字母的出现次数是否小于等于总长度的一半，按这种机制来取字母，不可能会剩下多余一个的相同的字母

class Solution {
public:
    string reorganizeString(string S) {
        string res = "";
        unordered_map<char, int> m;
        priority_queue<pair<int, char>> q;
        for (char c : S) ++m[c];
        for (auto a : m) {
            if (a.second > (S.size() + 1) / 2) return "";
            q.push({a.second, a.first});
        }
        while (q.size() >= 2) {
            auto t1 = q.top(); q.pop();
            auto t2 = q.top(); q.pop();
            res.push_back(t1.second);
            res.push_back(t2.second);
            if (--t1.first > 0) q.push(t1);
            if (--t2.first > 0) q.push(t2);
        }
        if (q.size() > 0) res.push_back(q.top().second);
        return res;
    }
};


```c++
class Solution {
public:
    string reorganizeString(string S) {
        string res = "";
        unordered_map<char, int> m;
        priority_queue<pair<int, char>> q;
        for (char c : S) ++m[c];
        for (auto a : m) {
            if (a.second > (S.size() + 1) / 2) return "";
            q.push({a.second, a.first});
        }
        while (q.size() >= 2) {
            auto t1 = q.top(); q.pop();
            auto t2 = q.top(); q.pop();
            res.push_back(t1.second);
            res.push_back(t2.second);
            if (--t1.first > 0) q.push(t1);
            if (--t2.first > 0) q.push(t2);
        }
        if (q.size() > 0) res.push_back(q.top().second);
        return res;
    }
};