LeetCode——动态规划整理（1）

目录

• 0-1 背包问题
  • 递归
  • 动态规划
    • Java
    • C++
• 分割等和子集
  • 动态规划
• 零钱兑换
  • HashMap 来当记忆数组的递归
  • 动态规划
  • 贪心 + DFS
• 零钱兑换 II
  • 递归
  • 动态规划
    • C++
    • python
    • C++
• 编辑距离
  • 递归
  • 动态规划
    • C++
    • python
• 鸡蛋掉落
  • 动态规划

0-1 背包问题

给你一个可装载重量为W的背包和N个物品，每个物品有重量和价值两个属性。其中第i个物品的重量为wt[i]，价值为val[i]，现在让你用这个背包装物品，最多能装的价值是多少？

举个简单的例子，输入如下：

N = 3, W = 4
wt = [2, 1, 3]
val = [4, 2, 3]

算法返回 6，选择前两件物品装进背包，总重量 3 小于W，可以获得最大价值 6。

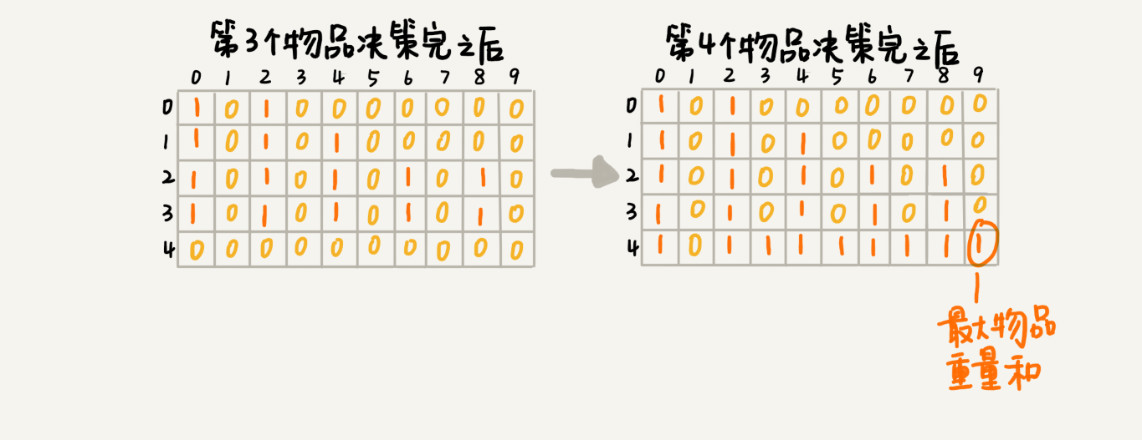
递归

private int maxW = Integer.MIN_VALUE; // 结果放到 maxW 中
private int[] weight = {2，2，4，6，3};  // 物品重量
private int n = 5; // 物品个数
private int w = 9; // 背包承受的最大重量
private boolean[][] mem = new boolean[5][10]; // 备忘录，默认值 false
public void f(int i, int cw) { // 调用 f(0, 0)
  if (cw == w || i == n) { // cw==w 表示装满了，i==n 表示物品都考察完了
    if (cw > maxW) maxW = cw;
    return;
  }
  if (mem[i][cw]) return; // 重复状态
  mem[i][cw] = true; // 记录 (i, cw) 这个状态
  f(i+1, cw); // 选择不装第 i 个物品
  if (cw + weight[i] <= w) {
    f(i+1,cw + weight[i]); // 选择装第 i 个物品
  }
}

动态规划

Java

//weight: 物品重量，n: 物品个数，w: 背包可承载重量

public int knapsack(int[] weight, int n, int w) {
  boolean[][] states = new boolean[n][w+1]; // 默认值 false
  states[0][0] = true;  // 第一行的数据要特殊处理，可以利用哨兵优化
  states[0][weight[0]] = true;
  for (int i = 1; i < n; ++i) { // 动态规划状态转移
    for (int j = 0; j <= w; ++j) {// 不把第 i 个物品放入背包
      if (states[i-1][j] == true) states[i][j] = states[i-1][j];
    }
    for (int j = 0; j <= w-weight[i]; ++j) {// 把第 i 个物品放入背包
      if (states[i-1][j]==true) states[i][j+weight[i]] = true;
    }
  }
  for (int i = w; i >= 0; --i) { // 输出结果
    if (states[n-1][i] == true) return i;
  }
  return 0;
}

C++

int knapsack(int W, int N, vector<int>& wt, vector<int>& val) {
    // vector 全填入 0，base case 已初始化
    vector<vector<int>> dp(N + 1, vector<int>(W + 1, 0));
    for (int i = 1; i <= N; i++) {
        for (int w = 1; w <= W; w++) {
            if (w - wt[i-1] < 0) {
                // 当前背包容量装不下，只能选择不装入背包
                dp[i][w] = dp[i - 1][w];
            } else {
                // 装入或者不装入背包，择优
                dp[i][w] = max(dp[i - 1][w - wt[i-1]] + val[i-1], dp[i - 1][w]);
            }
        }
    }

    return dp[N][W];
}

分割等和子集

给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

注意:

1. 每个数组中的元素不会超过 100
2. 数组的大小不会超过 200

示例 1:

输入: [1, 5, 11, 5]

输出: true

解释: 数组可以分割成 [1, 5, 5] 和 [11].

示例 2:

输入: [1, 2, 3, 5]

输出: false

解释: 数组不能分割成两个元素和相等的子集.

动态规划

二维

bool canPartition(vector<int>& nums) {
    int sum = 0;
    for (int num : nums) sum += num;
    // 和为奇数时，不可能划分成两个和相等的集合
    if (sum % 2 != 0) return false;
    int n = nums.size();
    sum = sum / 2;
    vector<vector<bool>> dp(n + 1, vector<bool>(sum + 1, false));
    // base case
    for (int i = 0; i <= n; i++)
        dp[i][0] = true;

    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= sum; j++) {
            if (j - nums[i - 1] < 0) {
               // 背包容量不足，不能装入第 i 个物品
                dp[i][j] = dp[i - 1][j]; 
            } else {
                // 装入或不装入背包
                dp[i][j] = dp[i - 1][j] | dp[i - 1][j-nums[i-1]];
            }
        }
    }
    return dp[n][sum];
}

一维

bool canPartition(vector<int>& nums) {
    int sum = 0, n = nums.size();
    for (int num : nums) sum += num;
    if (sum % 2 != 0) return false;
    sum = sum / 2;
    vector<bool> dp(sum + 1, false);
    // base case
    dp[0] = true;

    for (int i = 0; i < n; i++) 
        for (int j = sum; j >= 0; j--) 
            if (j - nums[i] >= 0) 
                dp[j] = dp[j] || dp[j - nums[i]];

    return dp[sum];
}

零钱兑换

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。

示例 1:

输入: coins = [1, 2, 5], amount = 11
输出: 3 
解释: 11 = 5 + 5 + 1

示例 2:

输入: coins = [2], amount = 3
输出: -1

说明:
你可以认为每种硬币的数量是无限的。

HashMap 来当记忆数组的递归

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        unordered_map<int, int> memo;
        memo[0] = 0;
        return coinChangeDFS(coins, amount, memo);
    }
    int coinChangeDFS(vector<int>& coins, int target, unordered_map<int, int>& memo) {
        if (target < 0) return - 1;
        if (memo.count(target)) return memo[target];
        int cur = INT_MAX;
        for (int i = 0; i < coins.size(); ++i) {
            int tmp = coinChangeDFS(coins, target - coins[i], memo);
            if (tmp >= 0) cur = min(cur, tmp + 1);
        }
        return memo[target] = (cur == INT_MAX) ? -1 : cur;
    }
};

动态规划

int change(int amount, int[] coins) {
    int n = coins.length;
    int[][] dp = amount int[n + 1][amount + 1];
    // base case
    for (int i = 0; i <= n; i++) 
        dp[i][0] = 1;

    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= amount; j++)
            if (j - coins[i-1] >= 0)
                dp[i][j] = dp[i - 1][j] 
                         + dp[i][j - coins[i-1]];
            else 
                dp[i][j] = dp[i - 1][j];
    }
    return dp[n][amount];
}

更新 dp[i] 的方法就是遍历每个硬币，如果遍历到的硬币值小于i值（比如不能用值为5的硬币去更新 dp[3]）时，用 dp[i - coins[j]] + 1 来更新 dp[i]，所以状态转移方程为：

dp[i] = min(dp[i], dp[i - coins[j]] + 1);

其中 coins[j] 为第j个硬币，而 i - coins[j] 为钱数i减去其中一个硬币的值，剩余的钱数在 dp 数组中找到值，然后加1和当前 dp 数组中的值做比较，取较小的那个更新 dp 数组。

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        vector<int> dp(amount + 1, amount + 1);
        dp[0] = 0;
        for (int i = 1; i <= amount; ++i) {
            for (int j = 0; j < coins.size(); ++j) {
                if (coins[j] <= i) {
                    dp[i] = min(dp[i], dp[i - coins[j]] + 1);
                }
            }
        }
        return (dp[amount] > amount) ? -1 : dp[amount];
    }
};

贪心 + DFS

1. 贪心

• 想要总硬币数最少，肯定是优先用大面值硬币，所以对 coins 按从大到小排序

• 先丢大硬币，再丢会超过总额时，就可以递归下一层丢的是稍小面值的硬币

2. 乘法对加法的加速

• 优先丢大硬币进去尝试，也没必要一个一个丢，可以用乘法算一下最多能丢几个

  k = amount / coins[c_index] 计算最大能投几个
  amount - k * coins[c_index] 减去扔了 k 个硬币
  count + k 加 k 个硬币

• 如果因为丢多了导致最后无法凑出总额，再回溯减少大硬币数量

3. 最先找到的并不是最优解

• 注意不是现实中发行的硬币，面值组合规划合理，会有奇葩情况

• 考虑到有 [1,7,10] 这种用例，按照贪心思路 10 + 1 + 1 + 1 + 1 会比 7 + 7 更早找到，所以还是需要把所有情况都递归完

4. ans 疯狂剪枝

• 贪心虽然得不到最优解，但也不是没用的
• 我们快速算出一个贪心的 ans 之后，虽然还会有奇葩情况，但是绝大部分普通情况就可以疯狂剪枝了

class Solution {
public:
    void coinChange(vector<int>& coins, int amount, int c_index, int count, int& ans){
        if (amount == 0){
            ans = min(ans, count);
            return;
        }
        if (c_index == coins.size()) return;

        for (int k = amount / coins[c_index]; k >= 0 && k + count < ans; k--){
            coinChange(coins, amount - k * coins[c_index], c_index + 1, count + k, ans);
        }
    }

    int coinChange(vector<int>& coins, int amount){
        if (amount == 0) return 0;
        sort(coins.rbegin(), coins.rend());
        int ans = INT_MAX;
        coinChange(coins, amount, 0, 0, ans);
        return ans == INT_MAX ? -1 : ans;
    }

};

零钱兑换 II

给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。

示例 1:

输入: amount = 5, coins = [1, 2, 5]
输出: 4
解释: 有四种方式可以凑成总金额:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1

示例 2:

输入: amount = 3, coins = [2]
输出: 0
解释: 只用面额2的硬币不能凑成总金额3。

示例 3:

输入: amount = 10, coins = [10] 
输出: 1

递归

class Solution {
public:
    int change(int amount, vector<int>& coins) {
        if (amount == 0) return 1;
        if (coins.empty()) return 0;
        map<pair<int, int>, int> memo;
        return helper(amount, coins, 0, memo);
    }
    int helper(int amount, vector<int>& coins, int idx, map<pair<int, int>, int>& memo) {
        if (amount == 0) return 1;
        else if (idx >= coins.size()) return 0;
        // 当用到最后一个硬币时，判断当前还剩的钱数是否能整除这个硬币，不能的话就返回0，否则返回1。
        else if (idx == coins.size() - 1) return amount % coins[idx] == 0;
        if (memo.count({amount, idx})) return memo[{amount, idx}];
        int val = coins[idx], res = 0;
        for (int i = 0; i * val <= amount; ++i) {
            int rem = amount - i * val;
            res += helper(rem, coins, idx + 1, memo);
        }
        return memo[{amount, idx}] = res;
    }
};

动态规划

	0	1	2	3
0	1	1	1	1
1	0	1	1	1
2	0	1	2	2
3	0	1	2	2
4	0	1	3	4
5	0	1	3	4

需要一个二维的 dp 数组，其中 dp[i][j] 表示用前i个硬币组成钱数为j的不同组合方法，怎么算才不会重复，也不会漏掉呢？

我们采用的方法是一个硬币一个硬币的增加，每增加一个硬币，都从1遍历到 amount，对于遍历到的当前钱数j，组成方法就是不加上当前硬币的拼法 dp[i-1][j]，还要加上，去掉当前硬币值的钱数的组成方法，当然钱数j要大于当前硬币值，状态转移方程也在上面的分析中得到了：

dp[i][j] = dp[i - 1][j] + (j >= coins[i - 1] ? dp[i][j - coins[i - 1]] : 0)

注意要初始化每行的第一个位置为0，参见代码如下：

C++

class Solution {
public:
    int change(int amount, vector<int>& coins) {
        vector<vector<int>> dp(coins.size() + 1, vector<int>(amount + 1, 0));
        dp[0][0] = 1;
        for (int i = 1; i <= coins.size(); ++i) {
            dp[i][0] = 1;
            for (int j = 1; j <= amount; ++j) {
                dp[i][j] = dp[i - 1][j] + (j >= coins[i - 1] ? dp[i][j - coins[i - 1]] : 0);
            }
        }
        return dp[coins.size()][amount];
    }
}; 

python

class Solution:
    def change(self, amount: int, coins: List[int]) -> int:
        dp = [[0 for _ in range(amount + 1)] for _ in range(len(coins) + 1)]
        # dp[i][j]的含义：
        # j代表所需要金额
        # i代表选到几种硬币，如
        # i=0代表一种硬币都不用，
        # i=1代表用coins[:1]类硬币（即只用coins[0]）,
        # i=2代表用coins[:2]类硬币（即只用coins[0],coins[1]）,以此类推
        # 初始化状态
        for c in range(1, amount + 1):
            dp[0][c] = 0  # 没有任何一种硬币，不论需要多少金额，都没有对应的方案数
        for r in range(len(coins) + 1):
            dp[r][0] = 1  # 如果金额为0，对多少种硬币来说都是1种方案
        for r in range(1, len(coins) + 1):
            for c in range(1, amount + 1):
                dp[r][c] = dp[r - 1][c]  # 不选当前指标r对应的硬币
                if c - coins[r - 1] >= 0:
                    dp[r][c] += dp[r][c - coins[r - 1]]  # 不选当前指标r对应的硬币
        return dp[-1][-1]

对空间进行优化，由于 dp[i][j] 仅仅依赖于 dp[i - 1][j] 和 dp[i][j - coins[i - 1]] 这两项，就可以使用一个一维dp数组来代替，此时的 dp[i] 表示组成钱数i的不同方法。

C++

class Solution {
public:
    int change(int amount, vector<int>& coins) {
        vector<int> dp(amount + 1, 0);
        dp[0] = 1;
        for (int coin : coins) {
            for (int i = coin; i <= amount; ++i) {
                dp[i] += dp[i - coin];
            }
        }
        return dp[amount];
    }
};

编辑距离

给你两个单词 word1 和 word2，请你计算出将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

1. 插入一个字符
2. 删除一个字符
3. 替换一个字符

示例 1：

输入：word1 = "horse", word2 = "ros"
输出：3
解释：
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

示例 2：

输入：word1 = "intention", word2 = "execution"
输出：5
解释：
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')

递归

class Solution {
public:
    int minDistance(string word1, string word2) {
        int m = word1.size(), n = word2.size();
        vector<vector<int>> memo(m, vector<int>(n));
        return helper(word1, 0, word2, 0, memo);
    }
    int helper(string& word1, int i, string& word2, int j, vector<vector<int>>& memo) {
        if (i == word1.size()) return (int)word2.size() - j;
        if (j == word2.size()) return (int)word1.size() - i;
        if (memo[i][j] > 0) return memo[i][j];
        int res = 0;
        if (word1[i] == word2[j]) {
            return helper(word1, i + 1, word2, j + 1, memo);
        } else {
            int insertCnt = helper(word1, i, word2, j + 1, memo);
            int deleteCnt = helper(word1, i + 1, word2, j, memo);
            int replaceCnt = helper(word1, i + 1, word2, j + 1, memo);
            res = min(insertCnt, min(deleteCnt, replaceCnt)) + 1;
        }
        return memo[i][j] = res;
    }
};

动态规划

	0	h	o	r	s	e
0	0	1	2	3	4	5
r	1	1	2	2	3	4
o	2	2	1	2	2	3
e	3	3	2	2	3	3

当 word1[i] == word2[j] 时，dp[i][j] = dp[i - 1][j - 1]，

其他情况时，dp[i][j] 是其左，左上，上的三个值中的最小值加1，其实这里的左，上，和左上，分别对应的增加，删除，修改操作，具体可以参见解法一种的讲解部分，那么可以得到状态转移方程为：

​ / dp[i - 1][j - 1] if word1[i - 1] == word2[j - 1]

dp[i][j] =

​ min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i][j - 1])) + 1 else

C++

class Solution {
public:
    int minDistance(string word1, string word2) {
        int m = word1.size(), n = word2.size();
        vector<vector<int>> dp(m + 1, vector<int>(n + 1));
        for (int i = 0; i <= m; ++i) dp[i][0] = i;
        for (int i = 0; i <= n; ++i) dp[0][i] = i;
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                if (word1[i - 1] == word2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    dp[i][j] = min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i][j - 1])) + 1;
                }
            }
        }
        return dp[m][n];
    }
};

python

int minDistance(String s1, String s2) {
    int m = s1.length(), n = s2.length();
    int[][] dp = new int[m + 1][n + 1];
    // base case 
    for (int i = 1; i <= m; i++)
        dp[i][0] = i;
    for (int j = 1; j <= n; j++)
        dp[0][j] = j;
    // 自底向上求解
    for (int i = 1; i <= m; i++)
        for (int j = 1; j <= n; j++)
            if (s1.charAt(i-1) == s2.charAt(j-1))
                dp[i][j] = dp[i - 1][j - 1];
            else               
                dp[i][j] = min(
                    dp[i - 1][j] + 1,
                    dp[i][j - 1] + 1,
                    dp[i-1][j-1] + 1
                );
    // 储存着整个 s1 和 s2 的最小编辑距离
    return dp[m][n];
}

int min(int a, int b, int c) {
    return Math.min(a, Math.min(b, c));
}

鸡蛋掉落

你将获得 K 个鸡蛋，并可以使用一栋从 1 到 N 共有 N 层楼的建筑。

每个蛋的功能都是一样的，如果一个蛋碎了，你就不能再把它掉下去。

你知道存在楼层 F ，满足 0 <= F <= N 任何从高于 F 的楼层落下的鸡蛋都会碎，从 F 楼层或比它低的楼层落下的鸡蛋都不会破。

每次移动，你可以取一个鸡蛋（如果你有完整的鸡蛋）并把它从任一楼层 X 扔下（满足 1 <= X <= N）。

你的目标是确切地知道 F 的值是多少。

无论 F 的初始值如何，你确定 F 的值的最小移动次数是多少？

示例 1：

输入：K = 1, N = 2
输出：2
解释：
鸡蛋从 1 楼掉落。如果它碎了，我们肯定知道 F = 0 。
否则，鸡蛋从 2 楼掉落。如果它碎了，我们肯定知道 F = 1 。
如果它没碎，那么我们肯定知道 F = 2 。
因此，在最坏的情况下我们需要移动 2 次以确定 F 是多少。

示例 2：

输入：K = 2, N = 6
输出：3

示例 3：

输入：K = 3, N = 14
输出：4

提示：

1. 1 <= K <= 100
2. 1 <= N <= 10000

动态规划

两个变量，鸡蛋数K和楼层数N，使用一个二维数组 DP，其中 dp[i][j] 表示有i个鸡蛋，j层楼要测需要的最小操作数。那么我们在任意k层扔鸡蛋的时候就有两种情况（注意这里的k跟鸡蛋总数K没有任何关系，k的范围是 [1, j]）：

• 鸡蛋碎掉：接下来就要用 i-1 个鸡蛋来测 k-1 层，所以需要 dp[i-1][k-1] 次操作。
• 鸡蛋没碎：接下来还可以用i个鸡蛋来测 j-k 层，所以需要 dp[i][j-k] 次操作。
  因为我们每次都要面对最坏的情况，所以在第j层扔，需要 max(dp[i-1][k-1], dp[i][j-k])+1 步，状态转移方程为：

dp[i][j] = min(dp[i][j], max(dp[i - 1][k - 1], dp[i][j - k]) + 1) ( 1 <= k <= j )

这种写法会超时 Time Limit Exceeded，OJ 对时间卡的还是蛮严格的，所以我们就需要想办法去优化时间复杂度。

这种写法里面我们枚举了 [1, j] 范围所有的k值，总时间复杂度为 O(KN^2)，若我们仔细观察 dp[i - 1][k - 1] 和 dp[i][j - k]，可以发现前者是随着k递增，后者是随着k递减，且每次变化的值最多为1，所以只要存在某个k值使得二者相等，那么就能得到最优解，否则取最相近的两个k值做比较，由于这种单调性，我们可以在 [1, j] 范围内对k进行二分查找，找到第一个使得 dp[i - 1][k - 1] 不小于 dp[i][j - k] 的k值，然后用这个k值去更新 dp[i][j] 即可，这样时间复杂度就减少到了 O(KNlgN)，其实也是险过，参见代码如下：

class Solution {
public:
    int superEggDrop(int K, int N) {
		vector<vector<int>> dp(K + 1, vector<int>(N + 1));
		for (int j = 1; j <= N; ++j) dp[1][j] = j;
		for (int i = 2; i <= K; ++i) {
			for (int j = 1; j <= N; ++j) {
				dp[i][j] = j;
				int left = 1, right = j;
				while (left < right) {
					int mid = left + (right - left) / 2;
					if (dp[i - 1][mid - 1] < dp[i][j - mid]) left = mid + 1;
					else right = mid;
				}
				dp[i][j] = min(dp[i][j], max(dp[i - 1][right - 1], dp[i][j - right]) + 1);
			}
		}
		return dp[K][N];
    }
};

对于固定的k，dp[i][j-k] 会随着j的增加而增加，最优决策点也会随着j单调递增，所以在每次移动j后，从上一次的最优决策点的位置来继续向后查找最优点即可，这样时间复杂度就优化到了 O(KN)，我们使用一个变量s表示当前的j值下的的最优决策点，然后当j值改变了，我们用一个 while 循环，来找到第下一个最优决策点s，使得 dp[i - 1][s - 1] 不小于 dp[i][j - s]，参见代码如下：

class Solution {
public:
    int superEggDrop(int K, int N) {
		vector<vector<int>> dp(K + 1, vector<int>(N + 1));
		for (int j = 1; j <= N; ++j) dp[1][j] = j;
		for (int i = 2; i <= K; ++i) {
			int s = 1;
			for (int j = 1; j <= N; ++j) {
				dp[i][j] = j;
				while (s < j && dp[i - 1][s - 1] < dp[i][j - s]) ++s;
				dp[i][j] = min(dp[i][j], max(dp[i - 1][s - 1], dp[i][j - s]) + 1);
			}
		}
		return dp[K][N];
    }
};

将问题转化一下，变成已知鸡蛋个数，和操作次数，求最多能测多少层楼的临界点。还是使用动态规划 来做，用一个二维 DP 数组，其中 dp[i][j] 表示当有i次操作，且有j个鸡蛋时能测出的最高的楼层数。再来考虑状态转移方程如何写，由于 dp[i][j] 表示的是在第i次移动且使用第j个鸡蛋测试第 dp[i-1][j-1]+1 层，因为上一个状态是第i-1次移动，且用第j-1个鸡蛋。此时还是有两种情况：

• 鸡蛋碎掉：说明至少可以测到的不会碎的层数就是 dp[i-1][j-1]。
• 鸡蛋没碎：那这个鸡蛋可以继续利用，此时我们还可以再向上查找 dp[i-1][j] 层。

那么加上当前层，总共可以通过i次操作和j个鸡蛋查找的层数范围是[0, dp[i-1][j-1] + dp[i-1][j] + 1]，这样就可以得到状态转移方程如下：

dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j] + 1

	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
0	0	0	0	0	0
1	0	1	2	3	4
2	0	1	3	6	10
3	0	1	3	7	14

当 dp[i][K] 正好小于N的时候，i就是我们要求的最小次数了，参见代码如下：

class Solution {
public:
    int superEggDrop(int K, int N) {
		vector<vector<int>> dp(N + 1, vector<int>(K + 1));
		int m = 0;
		while (dp[m][K] < N) {
			++m;
			for (int j = 1; j <= K; ++j) {
				dp[m][j] = dp[m - 1][j - 1] + dp[m - 1][j] + 1;
			}
		}
		return m;
    }
};

进一步的优化空间，因为当前的操作次数值的更新只跟上一次操作次数有关，所以我们并不需要保存所有的次数，可以使用一个一维数组，其中 dp[i] 表示当前次数下使用i个鸡蛋可以测出的最高楼层。状态转移方程的推导思路还是跟上面一样，参见代码如下：

class Solution {
public:
    int superEggDrop(int K, int N) {
		vector<int> dp(K + 1);
		int res = 0;
		for (; dp[K] < N; ++res) {
			for (int i = K; i > 0; --i) {
				dp[i] = dp[i] + dp[i - 1] + 1;
			}
		}
		return res;
    }
};