编译原理——实现一门脚本语言 原理篇（上）

正则文法和有限自动机

解析 age >= 45

词法分析示意图：

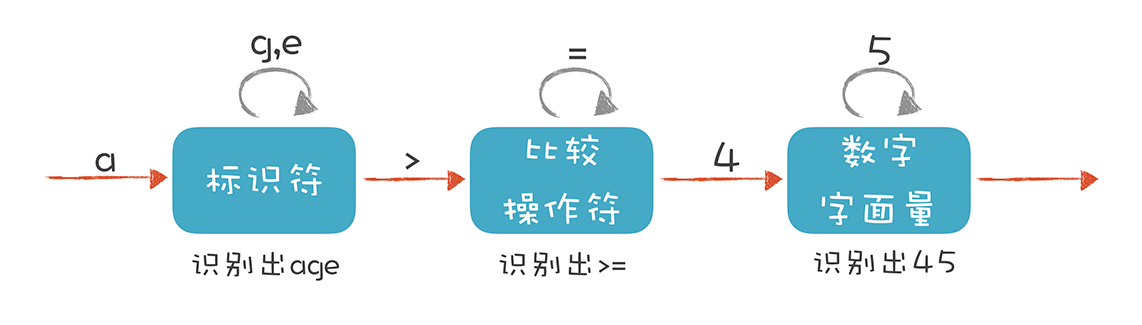
我们来描述一下标识符、比较操作符和数字字面量这三种Token的词法规则。

• 标识符：第一个字符必须是字母，后面的字符可以是字母或数字。
• 比较操作符：>和>=（其他比较操作符暂时忽略）。
• 数字字面量：全部由数字构成（像带小数点的浮点数，暂时不管它）。

我们就是依据这样的规则，来构造有限自动机的。这样，词法分析程序在遇到age、>=和45时，会分别识别成标识符、比较操作符和数字字面量。不过上面的图只是一个简化的示意图，一个严格意义上的有限自动机是下面这种画法：

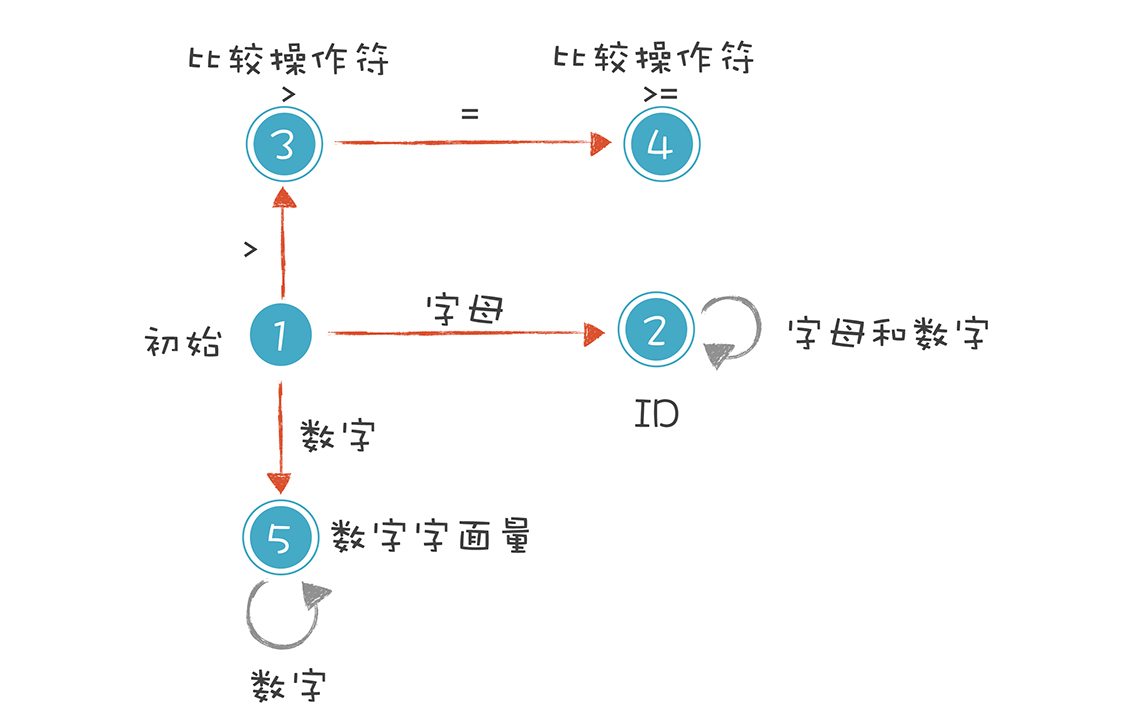
我来解释一下上图的5种状态。

1.初始状态：刚开始启动词法分析的时候，程序所处的状态。

2.标识符状态：在初始状态时，当第一个字符是字母的时候，迁移到状态2。当后续字符是字母和数字时，保留在状态2。如果不是，就离开状态2，写下该Token，回到初始状态。

3.大于操作符（GT）：在初始状态时，当第一个字符是>时，进入这个状态。它是比较操作符的一种情况。

4.大于等于操作符（GE）：如果状态3的下一个字符是=，就进入状态4，变成>=。它也是比较操作符的一种情况。

5.数字字面量：在初始状态时，下一个字符是数字，进入这个状态。如果后续仍是数字，就保持在状态5。

这里我想补充一下，你能看到上图中的圆圈有单线的也有双线的。双线的意思是这个状态已经是一个合法的Token了，单线的意思是这个状态还是临时状态。

按照这5种状态迁移过程，你很容易编成程序（我用Java写了代码示例，你可以用自己熟悉的语言编写）。我们先从状态1开始，在遇到不同的字符时，分别进入2、3、5三个状态：

DfaState nextState = DfaState.Initial;    //自动机的状态
if (isAlpha(ch)) {    //如果是字符，进入标识符状态
    nextState = DfaState.Id;
    token.type = TokenType.Identifier;
    tokenText.append(ch);
} else if (isDigit(ch)) {    //如果是数字，进入数字字面量状态
    nextState = DfaState.IntConstant;
    token.type = TokenType.IntConstant;
    tokenText.append(ch);
} else if (ch == '>') {
    nextState = DfaState.GT;
    token.type = TokenType.RelOp;
    tokenText.append(ch);
} else {
    nextState = DfaState.Initial;     // 暂时忽略其他的模式
}

上面的代码中，nextState是接下来要进入的状态。我用Java中的枚举（enum）类型定义了一些枚举值来代表不同的状态，让代码更容易读。

其中Token是自定义的一个数据结构，它有两个主要的属性：

一个是“type”，就是Token的类型，它用的也是一个枚举类型的值；

一个是“text”，也就是这个Token的文本值。

我们接着处理进入2、3、5三个状态之后的状态迁移过程：

while ((ich = reader.read()) != -1) {
    ch = (char) ich;
    switch (state) {
    case Initial:
        state = initToken(ch);  //重新确定后续状态
        break;
    case Id:
        if (isAlpha(ch) || isDigit(ch)) {
            tokenText.append(ch);    //保持标识符状态
        } else {
            state = initToken(ch);//退出标识符状态,保存Token
        }
        break;
    case GT:
        if (ch == '=') {
            token.type = TokenType.RelOp; 
            state = DfaState.GE;           //迁移到状态4
            tokenText.append(ch);
        } else {
            state = initToken(ch);//退出状态3，保存Token
        }
        break;
    case GE:
        state = initToken(ch);    //退出状态4，保存Token
        break;
    case IntConstant:
        if (isDigit(ch)) {
            tokenText.append(ch); //保持字符字面量状态   
        } else {
            state = initToken(ch);//退出字符字面量状态，存Token
        }
        break;
    }
}

运行这个示例程序，你就会成功地解析类似“age >= 45”这样的程序语句。不过，你可以先根据我的讲解自己实现一下，然后再去参考这个示例程序。

示例程序的输出如下，其中第一列是Token的类型，第二列是Token的文本值：

Identifier   age
GE           >=  
IntConstant  45  

上面的例子虽然简单，但其实已经讲清楚了词法原理，就是依据构造好的有限自动机，在不同的状态中迁移，从而解析出Token来。你只要再扩展这个有限自动机，增加里面的状态和迁移路线，就可以逐步实现一个完整的词法分析器了。

初识正则表达式

但是，这里存在一个问题。我们在描述词法规则时用了自然语言。比如，在描述标识符的规则时，我们是这样表达的：

第一个字符必须是字母，后面的字符可以是字母或数字。

这样描述规则并不精确，我们需要换一种严谨的表达方式，这种方式就是正则表达式。

上面的例子涉及了4种Token，这4种Token用正则表达式表达，是下面的样子：

Id :        [a-zA-Z_] ([a-zA-Z_] | [0-9])*
IntLiteral: [0-9]+
GT :        '>'
GE :        '>='

我先来解释一下这几个规则中用到的一些符号：

需要注意的是，不同语言的标识符、整型字面量的规则可能是不同的。比如，有的语言可以允许用Unicode作为标识符，也就是说变量名称可以是中文的。还有的语言规定，十进制数字字面量的第一位不能是0。这时候正则表达式会有不同的写法，对应的有限自动机自然也不同。而且，不同工具的正则表达式写法会略有不同，但大致是差不多的。

解析int age = 40，处理标识符和关键字规则的冲突

说完正则表达式，我们接着去处理其他词法，比如解析“int age = 40”这个语句，以这个语句为例研究一下词法分析中会遇到的问题：多个规则之间的冲突。

如果我们把这个语句涉及的词法规则用正则表达式写出来，是下面这个样子：

Int:        'int'
Id :        [a-zA-Z_] ([a-zA-Z_] | [0-9])*
Assignment : '='

这时候，你可能会发现这样一个问题：int这个关键字，与标识符很相似，都是以字母开头，后面跟着其他字母。

换句话说，int这个字符串，既符合标识符的规则，又符合int这个关键字的规则，这两个规则发生了重叠。这样就起冲突了，我们扫描字符串的时候，到底该用哪个规则呢？

当然，我们心里知道，int这个关键字的规则，比标识符的规则优先级高。普通的标识符是不允许跟这些关键字重名的。

在这里，我们来回顾一下：什么是关键字？

关键字是语言设计中作为语法要素的词汇，例如表示数据类型的int、char，表示程序结构的while、if，表述特殊数据取值的null、NAN等。

除了关键字，还有一些词汇叫保留字。保留字在当前的语言设计中还没用到，但是保留下来，因为将来会用到。我们命名自己的变量、类名称，不可以用到跟关键字和保留字相同的字符串。那么我们在词法分析器中，如何把关键字和保留字跟标识符区分开呢？

以“int age = 40”为例，我们把有限自动机修改成下面的样子，借此解决关键字和标识符的冲突。

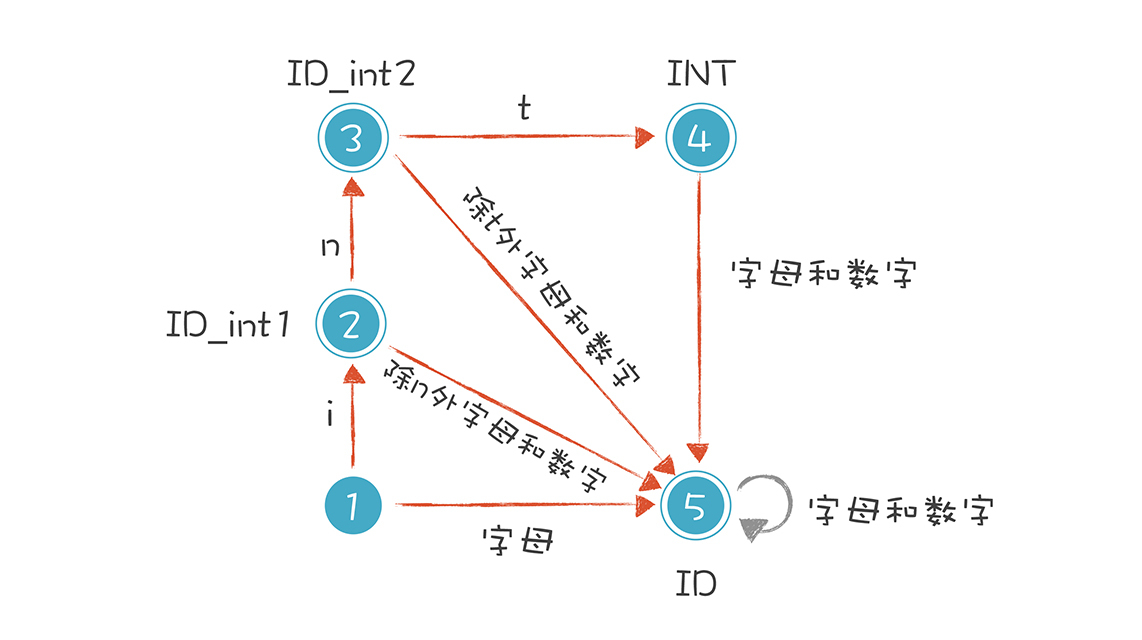
这个思路其实很简单。在识别普通的标识符之前，你先看看它是关键字还是保留字就可以了。具体做法是：

当第一个字符是i的时候，我们让它进入一个特殊的状态。接下来，如果它遇到n和t，就进入状态4。但这还没有结束，如果后续的字符还有其他的字母和数字，它又变成了普通的标识符。比如，我们可以声明一个intA（int和A是连着的）这样的变量，而不会跟int关键字冲突。

相应的代码也修改一下，文稿里的第一段代码要改成：

if (isAlpha(ch)) {
    if (ch == 'i') {
        newState = DfaState.Id_int1;  //对字符i特殊处理
    } else {
        newState = DfaState.Id;
    }
    ...  //后续代码
}

第二段代码要增加下面的语句：

case Id_int1:
    if (ch == 'n') {
        state = DfaState.Id_int2;
        tokenText.append(ch);
    }else if(isAlpha(ch) || isDigit(ch)){
        token.type = TokenType.Id; //变成标识符状态
        state = DfaState.Int;
    }else{
        token.type = TokenType.Id; 
        state = initToken(ch);     //记录下标识符i
        }
    break;
case Id_int2:
    if (ch == 't') {
        state = DfaState.Int;      //变成Int状态
        tokenText.append(ch);
    }else if(isAlpha(ch) || isDigit(ch)){
        token.type = TokenType.Id; //变成标识符状态
        state = DfaState.Int;
        tokenText.append(ch);
    }else{
        token.type = TokenType.Id;   
        state = initToken(ch);     //记录下标识符in
    }
    break;
case Int:
    if (!isAlpha(ch) && !isDigit(ch)) {
        token.type = TokenType.Int;
        state = initToken(ch);     //记录下关键字int
    }else{
        token.type = TokenType.Id;
        state = DfaState.Id;         //变成标识符状态
    }
    break;

接着，我们运行示例代码，就会输出下面的信息：

Int          int
Identifier   age
Assignment   =  
IntConstant  45  

而当你试着解析“intA = 10”程序的时候，会把intA解析成一个标识符。输出如下：

Identifier   intA
Assignment   =  
IntConstant  10  

解析算术表达式

解析完“int age = 40”之后，我们再按照上面的方法增加一些规则，这样就能处理算术表达式，例如“2+3*5”。 增加的词法规则如下：

Plus :  '+'
Minus : '-'
Star :  '*' 
Slash : '/'

然后再修改一下有限自动机和代码，就能解析“2+3*5”了，会得到下面的输出：

IntConstant  2
Plus         +  
IntConstant  3  
Star         *  
IntConstant  5  

文章的全部Code链接 提取码：e99j

纯手工打造公式计算器

我想你应该知道，公式是Excel电子表格软件的灵魂和核心。除此之外，在HR软件中，可以用公式自定义工资。而且，如果你要开发一款通用报表软件，也会大量用到自定义公式来计算报表上显示的数据。总而言之，很多高级一点儿的软件，都会用到自定义公式功能。

既然公式功能如此常见和重要，我们不妨实现一个公式计算器，给自己的软件添加自定义公式功能吧！

本节课将继续“手工打造”之旅，让你纯手工实现一个公式计算器，借此掌握语法分析的原理和递归下降算法（Recursive Descent Parsing），并初步了解上下文无关文法（Context-free Grammar，CFG）。

我所举例的公式计算器支持加减乘除算术运算，比如支持“2 + 3 * 5”的运算。

在学习语法分析时，我们习惯把上面的公式称为表达式。这个表达式看上去很简单，但你能借此学到很多语法分析的原理，例如左递归、优先级和结合性等问题。

当然了，要实现上面的表达式，你必须能分析它的语法。不过在此之前，我想先带你解析一下变量声明语句的语法，以便让你循序渐进地掌握语法分析。

解析变量声明语句：理解“下降”的含义

给出了一个简单的代码示例，也针对“int age = 45”这个语句，画了一个语法分析算法的示意图：

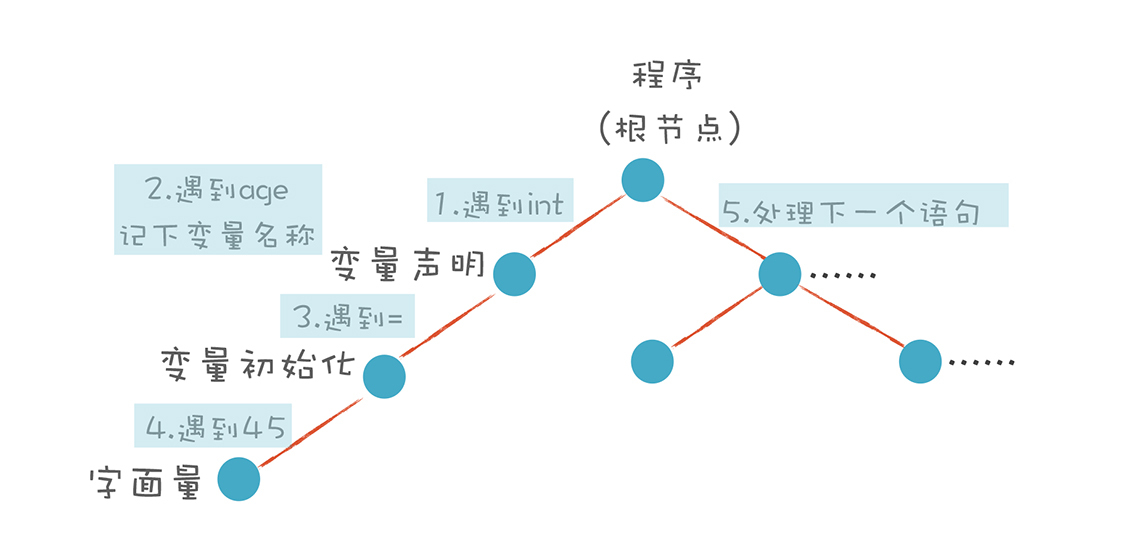
我们首先把变量声明语句的规则，用形式化的方法表达一下。它的左边是一个非终结符（Non-terminal）。右边是它的产生式（Production Rule）。在语法解析的过程中，左边会被右边替代。如果替代之后还有非终结符，那么继续这个替代过程，直到最后全部都是终结符（Terminal），也就是Token。只有终结符才可以成为AST的叶子节点。这个过程，也叫做推导（Derivation）过程：

intDeclaration : Int Identifier ('=' additiveExpression)?;

你可以看到，int类型变量的声明，需要有一个Int型的Token，加一个变量标识符，后面跟一个可选的赋值表达式。我们把上面的文法翻译成程序语句，伪代码如下：

//伪代码
MatchIntDeclare(){
  MatchToken(Int)；        //匹配Int关键字
  MatchIdentifier();       //匹配标识符
  MatchToken(equal);       //匹配等号
  MatchExpression();       //匹配表达式
}

实际代码在SimpleCalculator.java类的IntDeclare()方法中：

SimpleASTNode node = null;
Token token = tokens.peek();    //预读
if (token != null && token.getType() == TokenType.Int) {   //匹配Int
    token = tokens.read();      //消耗掉int
    if (tokens.peek().getType() == TokenType.Identifier) { //匹配标识符
        token = tokens.read();  //消耗掉标识符
        //创建当前节点，并把变量名记到AST节点的文本值中，
        //这里新建一个变量子节点也是可以的
        node = new SimpleASTNode(ASTNodeType.IntDeclaration, token.getText());
        token = tokens.peek();  //预读
        if (token != null && token.getType() == TokenType.Assignment) {
            tokens.read();      //消耗掉等号
            SimpleASTNode child = additive(tokens);  //匹配一个表达式
            if (child == null) {
                throw new Exception("invalide variable initialization, expecting an expression");
            }
            else{
                node.addChild(child);
            }
        }
    } else {
        throw new Exception("variable name expected");
    }
}

直白地描述一下上面的算法：

解析变量声明语句时，我先看第一个Token是不是int。如果是，那我创建一个AST节点，记下int后面的变量名称，然后再看后面是不是跟了初始化部分，也就是等号加一个表达式。我们检查一下有没有等号，有的话，接着再匹配一个表达式。

我们通常会对产生式的每个部分建立一个子节点，比如变量声明语句会建立四个子节点，分别是int关键字、标识符、等号和表达式。后面的工具就是这样严格生成AST的。但是我这里做了简化，只生成了一个子节点，就是表达式子节点。变量名称记到ASTNode的文本值里去了，其他两个子节点没有提供额外的信息，就直接丢弃了。

另外，从上面的代码中我们看到，程序是从一个Token的流中顺序读取。代码中的peek()方法是预读，只是读取下一个Token，但并不把它从Token流中移除。在代码中，我们用peek()方法可以预先看一下下一个Token是否是等号，从而知道后面跟着的是不是一个表达式。而read()方法会从Token流中移除，下一个Token变成了当前的Token。

这里需要注意的是，通过peek()方法来预读，实际上是对代码的优化，这有点儿预测的意味。我们后面会讲带有预测的自顶向下算法，它能减少回溯的次数。

我们把解析变量声明语句和表达式的算法分别写成函数。在语法分析的时候，调用这些函数跟后面的Token串做模式匹配。匹配上了，就返回一个AST节点，否则就返回null。如果中间发现跟语法规则不符，就报编译错误。

在这个过程中，上级文法嵌套下级文法，上级的算法调用下级的算法。表现在生成AST中，上级算法生成上级节点，下级算法生成下级节点。这就是“下降”的含义。

分析上面的伪代码和程序语句，你可以看到这样的特点：程序结构基本上是跟文法规则同构的。这就是递归下降算法的优点，非常直观。

接着说回来，我们继续运行这个示例程序，输出AST：

Programm Calculator
    IntDeclaration age
        AssignmentExp =
            IntLiteral 45

前面的文法和算法都很简单，这样级别的文法没有超出正则文法。也就是说，并没有超出我们做词法分析时用到的文法。

好了，解析完变量声明语句，带你理解了“下降”的含义之后，我们来看看如何用上下文无关文法描述算术表达式。

用上下文无关文法描述算术表达式

我们解析算术表达式的时候，会遇到更复杂的情况，这时，正则文法不够用，我们必须用上下文无关文法来表达。你可能会问：“正则文法为什么不能表示算术表达式？”别着急，我们来分析一下算术表达式的语法规则。

算术表达式要包含加法和乘法两种运算（简单起见，我们把减法与加法等同看待，把除法也跟乘法等同看待），加法和乘法运算有不同的优先级。我们的规则要能匹配各种可能的算术表达式：

• 2+3*5
• 2*3+5
• 2*3
• ……

思考一番之后，我们把规则分成两级：第一级是加法规则，第二级是乘法规则。把乘法规则作为加法规则的子规则，这样在解析形成AST时，乘法节点就一定是加法节点的子节点，从而被优先计算。

additiveExpression
    :   multiplicativeExpression
    |   additiveExpression Plus multiplicativeExpression
    ;

multiplicativeExpression
    :   IntLiteral
    |   multiplicativeExpression Star IntLiteral
    ;

你看，我们可以通过文法的嵌套，实现对运算优先级的支持。这样我们在解析“2 + 3 * 5”这个算术表达式时会形成类似下面的AST：

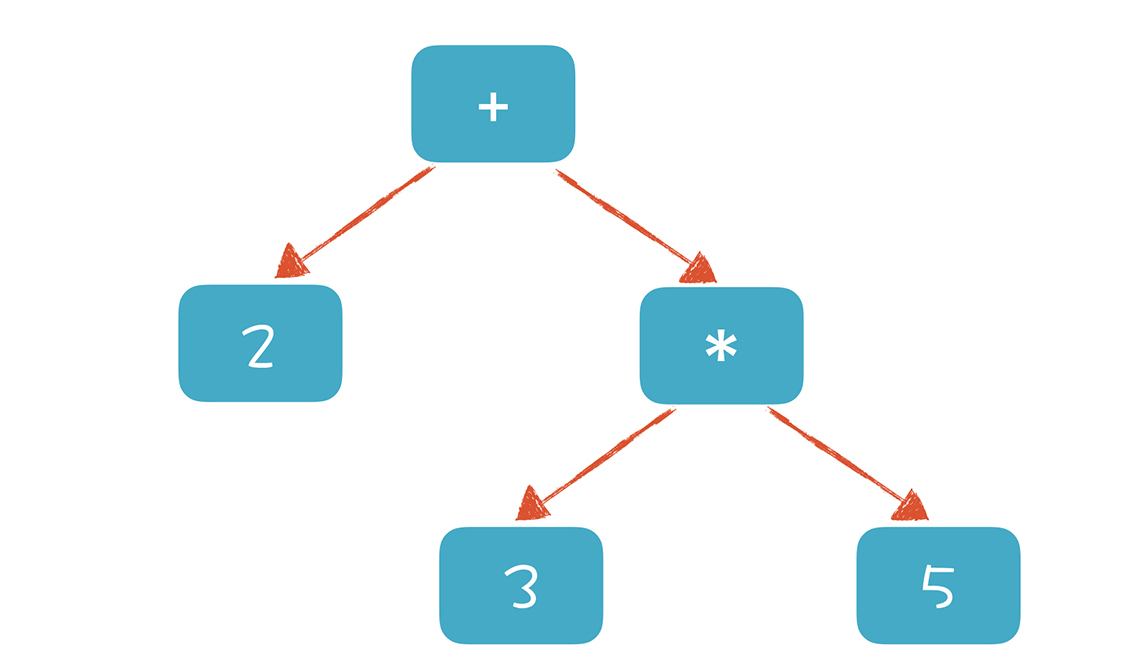
如果要计算表达式的值，只需要对根节点求值就可以了。为了完成对根节点的求值，需要对下级节点递归求值，所以我们先完成“3 * 5 = 15”，然后再计算“2 + 15 = 17”。

有了这个认知，我们在解析算术表达式的时候，便能拿加法规则去匹配。在加法规则中，会嵌套地匹配乘法规则。我们通过文法的嵌套，实现了计算的优先级。

应该注意的是，加法规则中还递归地又引用了加法规则。通过这种递归的定义，我们能展开、形成所有各种可能的算术表达式。比如“2+3*5” 的推导过程：

-->additiveExpression + multiplicativeExpression
-->multiplicativeExpression + multiplicativeExpression
-->IntLiteral + multiplicativeExpression
-->IntLiteral + multiplicativeExpression * IntLiteral 
-->IntLiteral + IntLiteral * IntLiteral

这种文法已经没有办法改写成正则文法了，它比正则文法的表达能力更强，叫做“上下文无关文法”。正则文法是上下文无关文法的一个子集。它们的区别呢，就是上下文无关文法允许递归调用，而正则文法不允许。

上下文无关的意思是，无论在任何情况下，文法的推导规则都是一样的。比如，在变量声明语句中可能要用到一个算术表达式来做变量初始化，而在其他地方可能也会用到算术表达式。不管在什么地方，算术表达式的语法都一样，都允许用加法和乘法，计算优先级也不变。好在你见到的大多数计算机语言，都能用上下文无关文法来表达它的语法。

那有没有上下文相关的情况需要处理呢？也是有的，但那不是语法分析阶段负责的，而是放在语义分析阶段来处理的。

解析算术表达式：理解“递归”的含义

在讲解上下文无关文法时，我提到了文法的递归调用，你也许会问，是否在算法上也需要递归的调用呢？要不怎么叫做“递归下降算法”呢？

的确，我们之前的算法只算是用到了“下降”，没有涉及“递归”，现在，我们就来看看如何用递归的算法翻译递归的文法。

我们先按照前面说的，把文法直观地翻译成算法。但是，我们遇到麻烦了。这个麻烦就是出现了无穷多次调用的情况。我们来看个例子。

在解析 “2 + 3”这样一个最简单的加法表达式的时候，我们直观地将其翻译成算法，结果出现了如下的情况：

• 首先匹配是不是乘法表达式，发现不是；
• 然后匹配是不是加法表达式，这里是递归调用；
• 会重复上面两步，无穷无尽。

“additiveExpression Plus multiplicativeExpression”这个文法规则的第一部分就递归地引用了自身，这种情况叫做左递归。通过上面的分析，我们知道左递归是递归下降算法无法处理的，这是递归下降算法最大的问题。

怎么解决呢？把“additiveExpression”调换到加号后面怎么样？我们来试一试。

additiveExpression
    :   multiplicativeExpression
    |   multiplicativeExpression Plus additiveExpression
    ;

我们接着改写成算法，这个算法确实不会出现无限调用的问题：

private SimpleASTNode additive(TokenReader tokens) throws Exception {
    SimpleASTNode child1 = multiplicative();  //计算第一个子节点
    SimpleASTNode node = child1;  //如果没有第二个子节点，就返回这个
    Token token = tokens.peek();
    if (child1 != null && token != null) {
        if (token.getType() == TokenType.Plus) {
            token = tokens.read();
            SimpleASTNode child2 = additive(); //递归地解析第二个节点
            if (child2 != null) {
                node = new SimpleASTNode(ASTNodeType.AdditiveExp, token.getText());
                node.addChild(child1);
                node.addChild(child2);
            } else {
                throw new Exception("invalid additive expression, expecting the right part.");
            }
        }
    }
    return node;
}

为了便于你理解，我解读一下上面的算法：

我们先尝试能否匹配乘法表达式，如果不能，那么这个节点肯定不是加法节点，因为加法表达式的两个产生式都必须首先匹配乘法表达式。遇到这种情况，返回null就可以了，调用者就这次匹配没有成功。如果乘法表达式匹配成功，那就再尝试匹配加号右边的部分，也就是去递归地匹配加法表达式。如果匹配成功，就构造一个加法的ASTNode返回。

同样的，乘法的文法规则也可以做类似的改写：

multiplicativeExpression
    :   IntLiteral
    |   IntLiteral Star multiplicativeExpression
    ;

现在我们貌似解决了左递归问题，运行这个算法解析 “2+3*5”，得到下面的AST：

Programm Calculator
    AdditiveExp +
        IntLiteral 2
        MulticativeExp *
            IntLiteral 3
            IntLiteral 5

是不是看上去一切正常？可如果让这个程序解析“2+3+4”呢？

Programm Calculator
    AdditiveExp +
        IntLiteral 2
        AdditiveExp +
            IntLiteral 3
            IntLiteral 4

问题是什么呢？计算顺序发生错误了。连续相加的表达式要从左向右计算，这是加法运算的结合性规则。但按照我们生成的AST，变成从右向左了，先计算了“3+4”，然后才跟“2”相加。这可不行！

为什么产生上面的问题呢？是因为我们修改了文法，把文法中加号左右两边的部分调换了一下。造成的影响是什么呢？你可以推导一下“2+3+4”的解析过程：

• 首先调用乘法表达式匹配函数multiplicative()，成功，返回了一个字面量节点2。
• 接着看看右边是否能递归地匹配加法表达式。
• 匹配的结果，真的返回了一个加法表达式“3+4”，这个变成了第二个子节点。错误就出在这里了。这样的匹配顺序，“3+4”一定会成为子节点，在求值时被优先计算。

所以，我们前面的方法其实并没有完美地解决左递归，因为它改变了加法运算的结合性规则。

实现表达式求值

上面帮助你理解了“递归”的含义，接下来，我要带你实现表达式的求值。其实，要实现一个表达式计算，只需要基于AST做求值运算。这个计算过程比较简单，只需要对这棵树做深度优先的遍历就好了。

深度优先的遍历也是一个递归算法。以上文中“2 + 3 * 5”的AST为例看一下。

• 对表达式的求值，等价于对AST根节点求值。
• 首先求左边子节点，算出是2。
• 接着对右边子节点求值，这时候需要递归计算下一层。计算完了以后，返回是15（3*5）。
• 把左右节点相加，计算出根节点的值17。

代码参见SimpleCalculator.Java中的evaluate()方法。

还是以“2+3*5”为例。它的求值过程输出如下，你可以看到求值过程中遍历了整棵树：

    Calculating: AdditiveExp          //计算根节点
        Calculating: IntLiteral      //计算第一个子节点
        Result: 2                     //结果是2
        Calculating: MulticativeExp   //递归计算第二个子节点
            Calculating: IntLiteral
            Result: 3
            Calculating: IntLiteral
            Result: 5
        Result: 15                //忽略递归的细节，得到结果是15
    Result: 17                    //根节点的值是17

解决二元表达式中的难点

简单地温习一下什么是左递归（Left Recursive）、优先级（Priority）和结合性（Associativity）。

在二元表达式的语法规则中，如果产生式的第一个元素是它自身，那么程序就会无限地递归下去，这种情况就叫做左递归。比如加法表达式的产生式“加法表达式 + 乘法表达式”，就是左递归的。而优先级和结合性则是计算机语言中与表达式有关的核心概念。它们都涉及了语法规则的设计问题。

我们要想深入探讨语法规则设计，需要像在词法分析环节一样，先了解如何用形式化的方法表达语法规则。“工欲善其事必先利其器”。熟练地阅读和书写语法规则，是我们在语法分析环节需要掌握的一项基本功。

书写语法规则，并进行推导

我们已经知道，语法规则是由上下文无关文法表示的，而上下文无关文法是由一组替换规则（又叫产生式）组成的，比如算术表达式的文法规则可以表达成下面这种形式：

add -> mul | add + mul
mul -> pri | mul * pri
pri -> Id | Num | (add) 

按照上面的产生式，add可以替换成mul，或者add + mul。这样的替换过程又叫做“推导”。以“2+3*5” 和 “2+3+4”这两个算术表达式为例，这两个算术表达式的推导过程分别如下图所示：

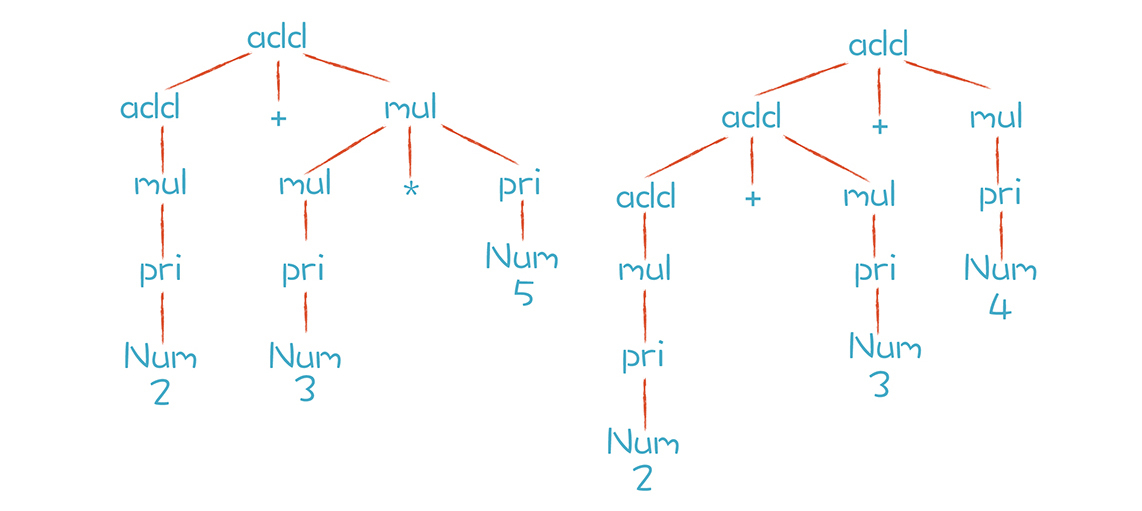
通过上图的推导过程，你可以清楚地看到这两个表达式是怎样生成的。而分析过程中形成的这棵树，其实就是AST。只不过我们手写的算法在生成AST的时候，通常会做一些简化，省略掉中间一些不必要的节点。比如，“add-add-mul-pri-Num”这一条分支，实际手写时会被简化成“add-Num”。其实，简化AST也是优化编译过程的一种手段，如果不做简化，呈现的效果就是上图的样子。

那么，上图中两颗树的叶子节点有哪些呢？Num、+和*都是终结符，终结符都是词法分析中产生的Token。而那些非叶子节点，就是非终结符。文法的推导过程，就是把非终结符不断替换的过程，让最后的结果没有非终结符，只有终结符。

而在实际应用中，语法规则经常写成下面这种形式：

add ::= mul | add + mul
mul ::= pri | mul * pri
pri ::= Id | Num | (add) 

这种写法叫做“巴科斯范式”，简称BNF。Antlr和Yacc这两个工具都用这种写法。为了简化书写把“::=”简化成一个冒号。

你有时还会听到一个术语，叫做扩展巴科斯范式(EBNF)。它跟普通的BNF表达式最大的区别，就是里面会用到类似正则表达式的一些写法。比如下面这个规则中运用了*号，来表示这个部分可以重复0到多次：

add -> mul (+ mul)*

其实这种写法跟标准的BNF写法是等价的，但是更简洁。为什么是等价的呢？因为一个项多次重复，就等价于通过递归来推导。从这里我们还可以得到一个推论：就是上下文无关文法包含了正则文法，比正则文法能做更多的事情。

确保正确的优先级

掌握了语法规则的写法之后，我们来看看如何用语法规则来保证表达式的优先级。刚刚，我们由加法规则推导到乘法规则，这种方式保证了AST中的乘法节点一定会在加法节点的下层，也就保证了乘法计算优先于加法计算。

听到这儿，你一定会想到，我们应该把关系运算（>、=、<）放在加法的上层，逻辑运算（and、or）放在关系运算的上层。的确如此，我们试着将它写出来：

exp -> or | or = exp   
or -> and | or || and
and -> equal | and && equal
equal -> rel | equal == rel | equal != rel
rel -> add | rel > add | rel < add | rel >= add | rel <= add
add -> mul | add + mul | add - mul 
mul -> pri | mul * pri | mul / pri 

这里表达的优先级从低到高是：赋值运算、逻辑运算（or）、逻辑运算（and）、相等比较（equal）、大小比较（rel）、加法运算（add）、乘法运算（mul）和基础表达式（pri）。

实际语言中还有更多不同的优先级，比如位运算等。而且优先级是能够改变的，比如我们通常会在语法里通过括号来改变计算的优先级。不过这怎么表达成语法规则呢？

其实，我们在最低层，也就是优先级最高的基础表达式（pri）这里，用括号把表达式包裹起来，递归地引用表达式就可以了。这样的话，只要在解析表达式的时候遇到括号，那么就知道这个是最优先的。这样的话就实现了优先级的改变：

pri -> Id | Literal | (exp)

了解了这些内容之后，到目前为止，你已经会写整套的表达式规则了，也能让公式计算器支持这些规则了。另外，在使用一门语言的时候，如果你不清楚各种运算确切的优先级，除了查阅常规的资料，你还多了一项新技能，就是阅读这门语言的语法规则文件，这些规则可能就是用BNF或EBNF的写法书写的。

弄明白优先级的问题以后，我们再来讨论一下结合性这个问题。

确保正确的结合性

在上一讲中，针对算术表达式写的第二个文法是错的，因为它的计算顺序是错的。“2+3+4”这个算术表达式，先计算了“3+4”然后才和“2”相加，计算顺序从右到左，正确的应该是从左往右才对。

这就是运算符的结合性问题。什么是结合性呢？同样优先级的运算符是从左到右计算还是从右到左计算叫做结合性。我们常见的加减乘除等算术运算是左结合的，“.”符号也是左结合的。

比如“rectangle.center.x” 是先获得长方形（rectangle）的中心点（center），再获得这个点的x坐标。计算顺序是从左向右的。那有没有右结合的例子呢？肯定是有的。赋值运算就是典型的右结合的例子。比如“x = y = 10”。

我们再来回顾一下“2+3+4”计算顺序出错的原因。用之前错误的右递归的文法解析这个表达式形成的简化版本的AST如下：

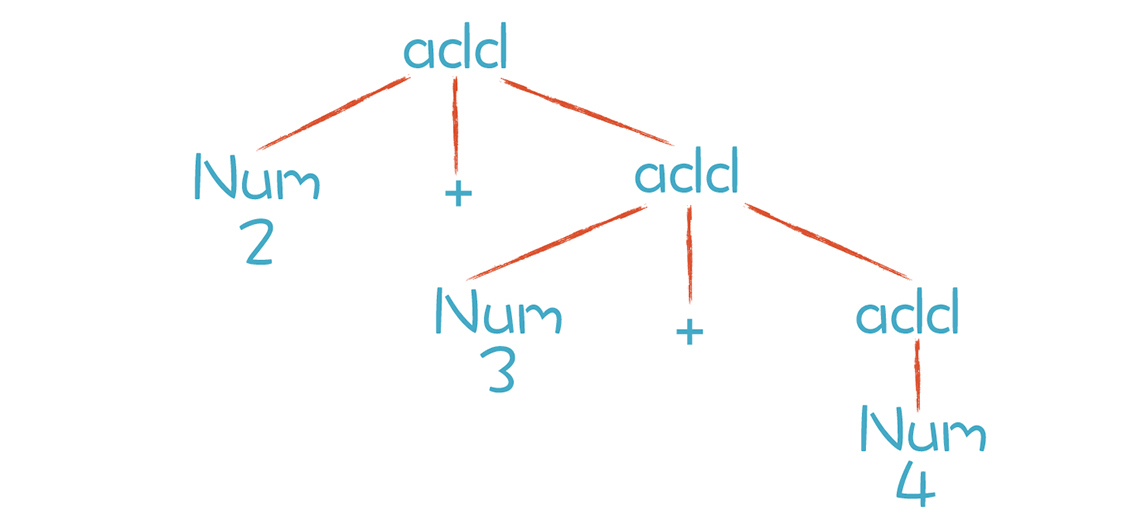
根据这个AST做计算会出现计算顺序的错误。不过如果我们将递归项写在左边，就不会出现这种结合性的错误。于是我们得出一个规律：对于左结合的运算符，递归项要放在左边；而右结合的运算符，递归项放在右边。

所以你能看到，我们在写加法表达式的规则的时候，是这样写的：

add -> mul | add + mul   

这是我们犯错之后所学到的知识。那么问题来了，大多数二元运算都是左结合的，那岂不是都要面临左递归问题？不用担心，我们可以通过改写左递归的文法，解决这个问题。

消除左递归

我提到过左递归的情况，也指出递归下降算法不能处理左递归。这里我要补充一点，并不是所有的算法都不能处理左递归，对于另外一些算法，左递归是没有问题的，比如LR算法。

消除左递归，用一个标准的方法，就能够把左递归文法改写成非左递归的文法。以加法表达式规则为例，原来的文法是“add -> add + mul”，现在我们改写成：

add -> mul add'
add' -> + mul add' | ε

文法中，ε（读作epsilon）是空集的意思。接下来，我们用刚刚改写的规则再次推导一下 “2+3+4”这个表达式，得到了下图中左边的结果：

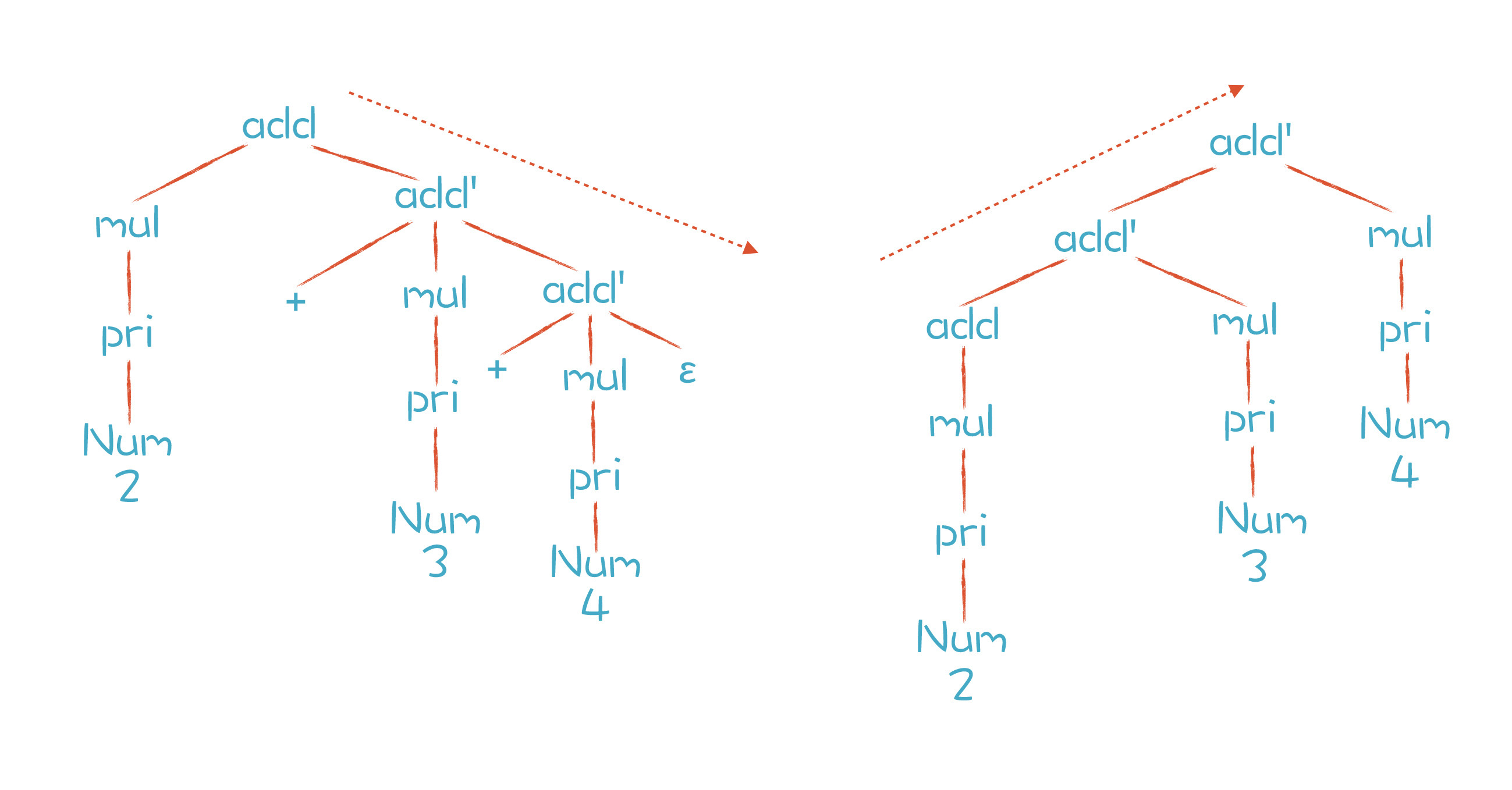
左边的分析树是推导后的结果。问题是，由于add’的规则是右递归的，如果用标准的递归下降算法，我们会跟上一讲一样，又会出现运算符结合性的错误。我们期待的AST是右边的那棵，它的结合性才是正确的。那么有没有解决办法呢？

答案是有的。我们仔细分析一下上面语法规则的推导过程。只有第一步是按照add规则推导，之后都是按照add’规则推导，一直到结束。

如果用EBNF方式表达，也就是允许用*号和+号表示重复，上面两条规则可以合并成一条：

add -> mul (+ mul)* 

写成这样有什么好处呢？能够优化我们写算法的思路。对于(+ mul)*这部分，我们其实可以写成一个循环，而不是一次次的递归调用。伪代码如下：

mul();
while(next token is +){
  mul()
  createAddNode
}

我们扩展一下话题。在研究递归函数的时候，有一个概念叫做尾递归，尾递归函数的最后一句是递归地调用自身。

编译程序通常都会把尾递归转化为一个循环语句，使用的原理跟上面的伪代码是一样的。相对于递归调用来说，循环语句对系统资源的开销更低，因此，把尾递归转化为循环语句也是一种编译优化技术。

好了，我们继续左递归的话题。现在我们知道怎么写这种左递归的算法了，大概是下面的样子：

private SimpleASTNode additive(TokenReader tokens) throws Exception {
    SimpleASTNode child1 = multiplicative(tokens);  //应用add规则
    SimpleASTNode node = child1;
    if (child1 != null) {
        while (true) {                              //循环应用add'
            Token token = tokens.peek();
            if (token != null && (token.getType() == TokenType.Plus || token.getType() == TokenType.Minus)) {
                token = tokens.read();              //读出加号
                SimpleASTNode child2 = multiplicative(tokens);  //计算下级节点
                node = new SimpleASTNode(ASTNodeType.Additive, token.getText());
                node.addChild(child1);              //注意，新节点在顶层，保证正确的结合性
                node.addChild(child2);
                child1 = node;
            } else {
                break;
            }
        }
    }
    return node;
}

修改完后，再次运行语法分析器分析“2+3+4+5”，会得到正确的AST：

Programm Calculator
    AdditiveExp +
        AdditiveExp +
        AdditiveExp +
            IntLiteral 2
            IntLiteral 3
                IntLiteral 4
        IntLiteral 5

这样，我们就把左递归问题解决了。

实现一门简单的脚本语言

继续实现一些功能，比如：

• 支持变量声明和初始化语句，就像“int age” “int age = 45”和“int age = 17+8+20”；
• 支持赋值语句“age = 45”；
• 在表达式中可以使用变量，例如“age + 10 *2”；
• 实现一个命令行终端，能够读取输入的语句并输出结果。

实现这些功能之后，我们的成果会更像一个脚本解释器。而且在这个过程中，我还会带你巩固语法分析中的递归下降算法，和你一起讨论“回溯”这个特征，让你对递归下降算法的特征理解得更加全面。

不过，为了实现这些新的语法，我们首先要把它们用语法规则描述出来。

增加所需要的语法规则

首先，一门脚本语言是要支持语句的，比如变量声明语句、赋值语句等等。单独一个表达式，也可以视为语句，叫做“表达式语句”。你在终端里输入2+3；，就能回显出5来，这就是表达式作为一个语句在执行。按照我们的语法，无非是在表达式后面多了个分号而已。C语言和Java都会采用分号作为语句结尾的标识，我们也可以这样写。

我们用扩展巴科斯范式（EBNF）写出下面的语法规则：

programm: statement+;  

statement
: intDeclaration
| expressionStatement
| assignmentStatement
;

变量声明语句以int开头，后面跟标识符，然后有可选的初始化部分，也就是一个等号和一个表达式，最后再加分号：

intDeclaration : 'int' Identifier ( '=' additiveExpression)? ';';

表达式语句目前只支持加法表达式，未来可以加其他的表达式，比如条件表达式，它后面同样加分号：

expressionStatement : additiveExpression ';';

赋值语句是标识符后面跟着等号和一个表达式，再加分号：

assignmentStatement : Identifier '=' additiveExpression ';';

为了在表达式中可以使用变量，我们还需要把primaryExpression改写，除了包含整型字面量以外，还要包含标识符和用括号括起来的表达式：

primaryExpression : Identifier| IntLiteral | '(' additiveExpression ')';

这样，我们就把想实现的语法特性，都用语法规则表达出来了。接下来，我们就一步一步实现这些特性。

让脚本语言支持变量

之前实现的公式计算器只支持了数字字面量的运算，如果能在表达式中用上变量，会更有用，比如能够执行下面两句：

int age = 45;
age + 10 * 2;

这两个语句里面的语法特性包含了变量声明、给变量赋值，以及在表达式里引用变量。为了给变量赋值，我们必须在脚本语言的解释器中开辟一个存储区，记录不同的变量和它们的值：

private HashMap<String, Integer> variables = new HashMap<String, Integer>();

我们简单地用了一个HashMap作为变量存储区。在变量声明语句和赋值语句里，都可以修改这个变量存储区中的数据，而获取变量值可以采用下面的代码：

if (variables.containsKey(varName)) {
    Integer value = variables.get(varName);  //获取变量值
    if (value != null) {
        result = value;                      //设置返回值
    } else {                                 //有这个变量，没有值
        throw new Exception("variable " + varName + " has not been set any value");
    }
}
else{ //没有这个变量。
    throw new Exception("unknown variable: " + varName);
}

通过这样的一个简单的存储机制，我们就能支持变量了。当然，这个存储机制可能过于简单了，我们后面讲到作用域的时候，这么简单的存储机制根本不够。不过目前我们先这么用着，以后再考虑改进它。

解析赋值语句

接下来，我们来解析赋值语句，例如“age = age + 10 * 2；”：

private SimpleASTNode assignmentStatement(TokenReader tokens) throws Exception {
    SimpleASTNode node = null;
    Token token = tokens.peek();    //预读，看看下面是不是标识符
    if (token != null && token.getType() == TokenType.Identifier) {
        token = tokens.read();      //读入标识符
        node = new SimpleASTNode(ASTNodeType.AssignmentStmt, token.getText());
        token = tokens.peek();      //预读，看看下面是不是等号
        if (token != null && token.getType() == TokenType.Assignment) {
            tokens.read();          //取出等号
            SimpleASTNode child = additive(tokens);
            if (child == null) {    //出错，等号右面没有一个合法的表达式
                throw new Exception("invalide assignment statement, expecting an expression");
            }
            else{
                node.addChild(child);   //添加子节点
                token = tokens.peek();  //预读，看看后面是不是分号
                if (token != null && token.getType() == TokenType.SemiColon) {
                    tokens.read();      //消耗掉这个分号

                } else {            //报错，缺少分号
                    throw new Exception("invalid statement, expecting semicolon");
                }
            }
        }
        else {
            tokens.unread();    //回溯，吐出之前消化掉的标识符
            node = null;
        }
    }
    return node;
}

为了方便你理解，我来解读一下上面这段代码的逻辑：

我们既然想要匹配一个赋值语句，那么首先应该看看第一个Token是不是标识符。

如果不是，那么就返回null，匹配失败。

如果第一个Token确实是标识符，我们就把它消耗掉，接着看后面跟着的是不是等号。

如果不是等号，那证明我们这个不是一个赋值语句，可能是一个表达式什么的。那么我们就要回退刚才消耗掉的Token，就像什么都没有发生过一样，并且返回null。

回退的时候调用的方法就是unread()。

如果后面跟着的确实是等号，那么在继续看后面是不是一个表达式，表达式后面跟着的是不是分号。

如果不是，就报错就好了。这样就完成了对赋值语句的解析。

利用上面的代码，我们还可以改造一下变量声明语句中对变量初始化的部分，让它在初始化的时候支持表达式，因为这个地方跟赋值语句很像，例如“int newAge = age + 10 * 2；”。

理解递归下降算法中的回溯

在设计语法规则的过程中，其实故意设计了一个陷阱，这个陷阱能帮我们更好地理解递归下降算法的一个特点：回溯。理解这个特点能帮助你更清晰地理解递归下降算法的执行过程，从而再去想办法优化它。

考虑一下age = 45；这个语句。肉眼看过去，你马上知道它是个赋值语句，但是当我们用算法去做模式匹配时，就会发生一些特殊的情况。看一下我们对statement语句的定义：

statement
: intDeclaration
| expressionStatement
| assignmentStatement
;

我们首先尝试intDeclaration，但是age = 45；语句不是以int开头的，所以这个尝试会返回null。然后我们接着尝试expressionStatement，看一眼下面的算法：

private SimpleASTNode expressionStatement() throws Exception {
        int pos = tokens.getPosition();  //记下初始位置
        SimpleASTNode node = additive(); //匹配加法规则
        if (node != null) {
            Token token = tokens.peek();
            if (token != null && token.getType() == TokenType.SemiColon) {   //要求一定以分号结尾
                tokens.read();
            } else {
                node = null;
                tokens.setPosition(pos); // 回溯
            }
        }
        return node;
    }

出现了什么情况呢？age = 45；语句最左边是一个标识符。根据我们的语法规则，标识符是一个合法的addtiveExpresion，因此additive()函数返回一个非空值。接下来，后面应该扫描到一个分号才对，但是显然不是，标识符后面跟的是等号，这证明模式匹配失败。

失败了该怎么办呢？我们的算法一定要把Token流的指针拨回到原来的位置，就像一切都没发生过一样。因为我们不知道addtive()这个函数往下尝试了多少步，因为它可能是一个很复杂的表达式，消耗掉了很多个Token，所以我们必须记下算法开始时候的位置，并在失败时回到这个位置。尝试一个规则不成功之后，恢复到原样，再去尝试另外的规则，这个现象就叫做“回溯”。

因为有可能需要回溯，所以递归下降算法有时会做一些无用功。在assignmentStatement的算法中，我们就通过unread()，回溯了一个Token。而在expressionStatement中，我们不确定要回溯几步，只好提前记下初始位置。匹配expressionStatement失败后，算法去尝试匹配assignmentStatement。这次获得了成功。

试探和回溯的过程，是递归下降算法的一个典型特征。通过上面的例子，你应该对这个典型特征有了更清晰的理解。递归下降算法虽然简单，但它通过试探和回溯，却总是可以把正确的语法匹配出来，这就是它的强大之处。当然，缺点是回溯会拉低一点儿效率。但我们可以在这个基础上进行改进和优化，实现带有预测分析的递归下降，以及非递归的预测分析。有了对递归下降算法的清晰理解，我们去学习其他的语法分析算法的时候，也会理解得更快。

我们接着再讲回溯牵扯出的另一个问题：什么时候该回溯，什么时候该提示语法错误？

大家在阅读示例代码的过程中，应该发现里面有一些错误处理的代码，并抛出了异常。比如在赋值语句中，如果等号后面没有成功匹配一个加法表达式，我们认为这个语法是错的。因为在我们的语法中，等号后面只能跟表达式，没有别的可能性。

token = tokens.read();          //读出等号
node = additive();    //匹配一个加法表达式
if (node == null) {
    //等号右边一定需要有另一个表达式  
    throw new Exception("invalide assignment expression, expecting an additive expression");
}

你可能会意识到一个问题，当我们在算法中匹配不成功的时候，我们前面说的是应该回溯呀，应该再去尝试其他可能性呀，为什么在这里报错了呢？换句话说，什么时候该回溯，什么时候该提示这里发生了语法错误呢？

其实这两种方法最后的结果是一样的。我们提示语法错误的时候，是说我们知道已经没有其他可能的匹配选项了，不需要浪费时间去回溯。就比如，在我们的语法中，等号后面必然跟表达式，否则就一定是语法错误。你在这里不报语法错误，等试探完其他所有选项后，还是需要报语法错误。所以说，提前报语法错误，实际上是我们写算法时的一种优化。

在写编译程序的时候，我们不仅仅要能够解析正确的语法，还要尽可能针对语法错误提供友好的提示，帮助用户迅速定位错误。错误定位越是准确、提示越是友好，我们就越喜欢它。

好了，到目前为止，已经能够能够处理几种不同的语句，如变量声明语句，赋值语句、表达式语句，那么我们把所有这些成果放到一起，来体会一下使用自己的脚本语言的乐趣吧！

我们需要一个交互式的界面来输入程序，并执行程序，这个交互式的界面就叫做REPL。

实现一个简单的REPL

脚本语言一般都会提供一个命令行窗口，让你输入一条一条的语句，马上解释执行它，并得到输出结果，比如Node.js、Python等都提供了这样的界面。这个输入、执行、打印的循环过程就叫做REPL（Read-Eval-Print Loop）。你可以在REPL中迅速试验各种语句，REPL即时反馈的特征会让你乐趣无穷。所以，即使是非常资深的程序员，也会经常用REPL来验证自己的一些思路，它相当于一个语言的PlayGround（游戏场），是个必不可少的工具。

在SimpleScript.java中，我们也实现了一个简单的REPL。基本上就是从终端一行行的读入代码，当遇到分号的时候，就解释执行，代码如下：

SimpleParser parser = new SimpleParser();
SimpleScript script = new SimpleScript();
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));   //从终端获取输入

String scriptText = "";
System.out.print("
>");   //提示符

while (true) {             //无限循环
    try {
        String line = reader.readLine().trim(); //读入一行
        if (line.equals("exit();")) {   //硬编码退出条件
            System.out.println("good bye!");
            break;
        }
        scriptText += line + "
";
        if (line.endsWith(";")) { //如果没有遇到分号的话，会再读一行
            ASTNode tree = parser.parse(scriptText); //语法解析
            if (verbose) {
                parser.dumpAST(tree, "");
            }
          
            script.evaluate(tree, ""); //对AST求值，并打印

            System.out.print("
>");   //显示一个提示符

            scriptText = "";
        }

    } catch (Exception e) { //如果发现语法错误，报错，然后可以继续执行
        System.out.println(e.getLocalizedMessage());
        System.out.print("
>");   //提示符
        scriptText = "";
    } 
}

运行java craft.SimpleScript，你就可以在终端里尝试各种语句了。如果是正确的语句，系统马上会反馈回结果。如果是错误的语句，REPL还能反馈回错误信息，并且能够继续处理下面的语句。我们前面添加的处理语法错误的代码，现在起到了作用！下面是在我电脑上的运行情况：

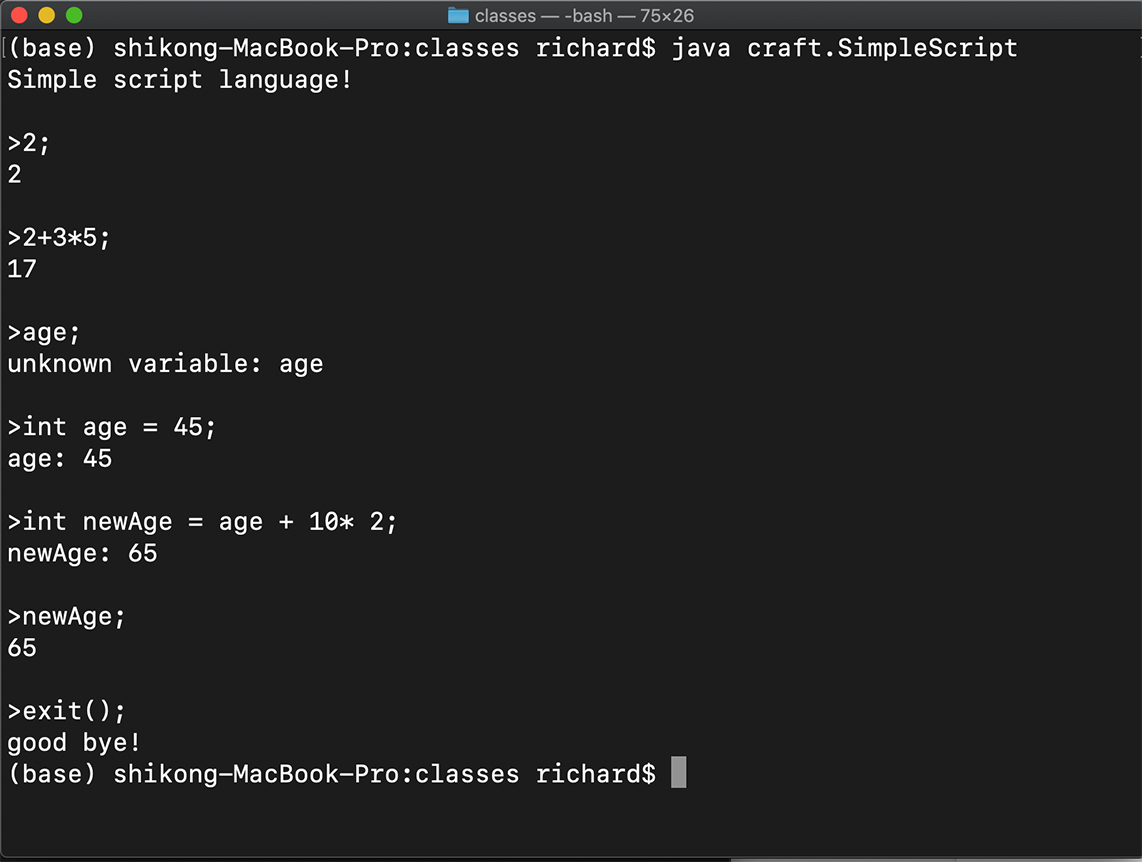
如果你用java craft.SimpleScript -v启动REPL，则进入Verbose模式，它还会每次打印出AST，你可以尝试一下。

退出REPL需要在终端输入ctl+c，或者调用exit()函数。我们目前的解释器并没有支持函数，所以我们是在REPL里硬编码来实现exit()函数的。后面的课程里，我会带你真正地实现函数特性。

用Antlr生成词法、语法分析器

前面重点讲解了词法分析和语法分析，在例子中提到的词法和语法规则也是高度简化的。虽然这些内容便于理解原理，也能实现一个简单的原型，在实际应用中却远远不够。实际应用中，一个完善的编译程序还要在词法方面以及语法方面实现很多工作，这里特意画了一张图，可以直观地看一下。

如果让编译程序实现上面这么多工作，完全手写效率会有点儿低，那么我们有什么方法可以提升效率呢？答案是借助工具。

编译器前端工具有很多，比如Lex（以及GNU的版本Flex）、Yacc（以及GNU的版本Bison）、JavaCC等等。我们只讲Antlr，主要有两个原因。

• Antlr能支持更广泛的目标语言，包括Java、C#、JavaScript、Python、Go、C++、Swift。无论你用上面哪种语言，都可以用它生成词法和语法分析的功能。而我们就使用它生成了Java语言和C++语言两个版本的代码。

• Antlr的语法更加简单。它能把类似左递归的一些常见难点在工具中解决，对提升工作效率有很大的帮助。这一点，你会在后面的课程中直观地感受到。

而我们今天的目标就是了解Antlr，然后能够使用Antlr生成词法分析器与语法分析器。

接下来，先来了解一下Antlr这个工具。

初识Antlr

Antlr是一个开源的工具，支持根据规则文件生成词法分析器和语法分析器，它自身是用Java实现的。

你可以下载Antlr工具，并根据说明做好配置。同时，你还需要配置好机器上的Java环境（可以在Oracle官网找到最新版本的JDK）。

GitHub上还有很多供参考的语法规则，你可以下载到本地硬盘随时查阅。

接下来，我带你实际用一用Antlr，让你用更轻松的方式生成词法分析器和语法分析器。

用Antlr生成词法分析器

Antlr通过解析规则文件来生成编译器。规则文件以.g4结尾，词法规则和语法规则可以放在同一个文件里。不过为了清晰起见，我们还是把它们分成两个文件，先用一个文件编写词法规则。

为了让你快速进入状态，我们先做一个简单的练习预热一下。我们创建一个Hello.g4文件，用于保存词法规则，然后把之前用过的一些词法规则写进去。

lexer grammar Hello;  //lexer关键字意味着这是一个词法规则文件，名称是Hello，要与文件名相同

//关键字
If :               'if';
Int :              'int';

//字面量
IntLiteral:        [0-9]+;
StringLiteral:      '"' .*? '"' ;  //字符串字面量

//操作符
AssignmentOP:       '=' ;    
RelationalOP:       '>'|'>='|'<' |'<=' ;    
Star:               '*';
Plus:               '+';
Sharp:              '#';
SemiColon:          ';';
Dot:                '.';
Comm:               ',';
LeftBracket :       '[';
RightBracket:       ']';
LeftBrace:          '{';
RightBrace:         '}';
LeftParen:          '(';
RightParen:         ')';

//标识符
Id :                [a-zA-Z_] ([a-zA-Z_] | [0-9])*;

//空白字符，抛弃
Whitespace:         [ 	]+ -> skip;
Newline:            ( '
' '
'?|'
')-> skip;

你能很直观地看到，每个词法规则都是大写字母开头，这是Antlr对词法规则的约定。而语法规则是以小写字母开头的。其中，每个规则都是用我们已经了解的正则表达式编写的。

接下来，我们来编译词法规则，在终端中输入命令：

antlr Hello.g4

这个命令是让Antlr编译规则文件，并生成Hello.java文件和其他两个辅助文件。你可以打开看一看文件里面的内容。接着，我用下面的命令编译Hello.java：

javac *.java

结果会生成Hello.class文件，这就是我们生成的词法分析器。接下来，我们来写个脚本文件，让生成的词法分析器解析一下：

int age = 45;
if (age >= 17+8+20){
  printf("Hello old man!");
}

我们将上面的脚本存成hello.play文件，然后在终端输入下面的命令：

grun Hello tokens -tokens hello.play

grun命令实际上是调用了我们刚才生成的词法分析器，即Hello类，打印出对hello.play词法分析的结果：

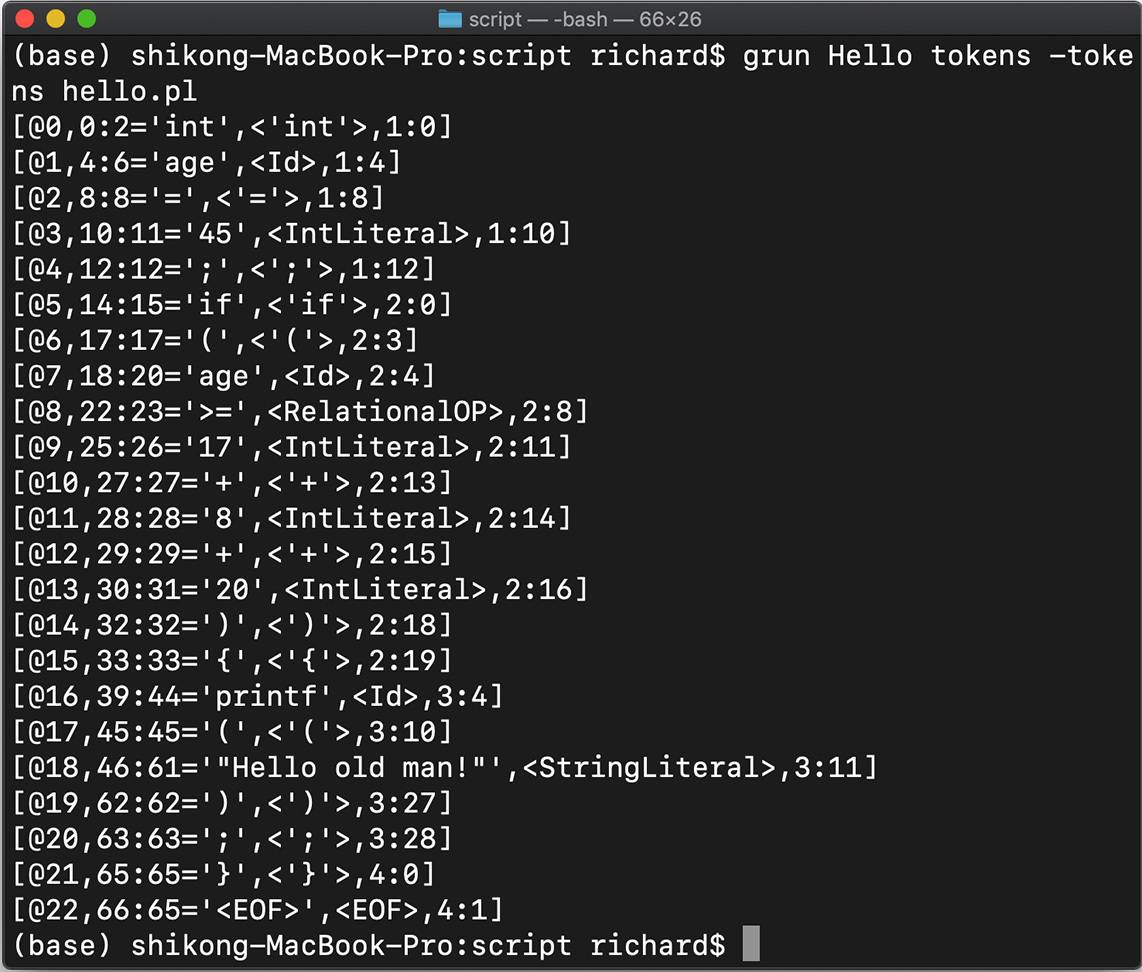
从结果中看到，我们的词法分析器把每个Token都识别了，还记录了它们在代码中的位置、文本值、类别。上面这些都是Token的属性。

以第二行[@1, 4:6=‘age’,< Id >,1:4]为例，其中@1是Token的流水编号，表明这是1号Token；4:6是Token在字符流中的开始和结束位置；age是文本值，Id是其Token类别；最后的1:4表示这个Token在源代码中位于第1行、第4列。

非常好，现在我们已经让Antlr顺利跑起来了！接下来，让词法规则更完善、更严密一些吧！怎么做呢？当然是参考成熟的规则文件。

从Antlr的一些示范性的规则文件中，我选了Java的作为参考。先看看我们之前写的字符串字面量的规则：

StringLiteral:      '"' .*? '"' ;  //字符串字面量

我们的版本相当简化，就是在双引号可以包含任何字符。可这在实际中不大好用，因为连转义功能都没有提供。我们对于一些不可见的字符，比如回车，要提供转义功能，如“ ”。同时，如果字符串里本身有双引号的话，也要将它转义，如“”。Unicode也要转义。最后，转义字符本身也需要转义，如“”。

下面这一段内容是Java语言中的字符串字面量的完整规则。你可以看一下文稿，这个规则就很细致了，把各种转义的情况都考虑进去了：

STRING_LITERAL:     '"' (~["\
] | EscapeSequence)* '"';

fragment EscapeSequence
    : '\' [btnfr"'\]
    | '\' ([0-3]? [0-7])? [0-7]
    | '\' 'u'+ HexDigit HexDigit HexDigit HexDigit
    ;

fragment HexDigit
    : [0-9a-fA-F]
    ;  

在这个规则文件中，fragment指的是一个语法片段，是为了让规则定义更清晰。它本身并不生成Token，只有StringLiteral规则才会生成Token。

当然了，除了字符串字面量，数字字面量、标识符的规则也可以定义得更严密。不过，因为这些规则文件都很严密，写出来都很长，在这里我就不一一展开了。如果感兴趣，我推荐你在下载的规则文件中找到这些部分看一看。你还可以参考不同作者写的词法规则，体会一下他们的设计思路。和高手过招，会更快地提高你的水平。

在带你借鉴了成熟的规则文件之后，想穿插性地讲解一下在词法规则中对Token归类的问题。在设计词法规则时，你经常会遇到这个问题，解决这个问题，词法规则会更加完善。

在前面练习的规则文件中，我们把>=、>、<都归类为关系运算符，算作同一类Token，而+、*等都单独作为另一类Token。那么，哪些可以归并成一类，哪些又是需要单独列出的呢？

其实，这主要取决于语法的需要。也就是在语法规则文件里，是否可以出现在同一条规则里。它们在语法层面上没有区别，只是在语义层面上有区别。

比如，加法和减法虽然是不同的运算，但它们可以同时出现在同一条语法规则中，它们在运算时的特性完全一致，包括优先级和结合性，乘法和除法可以同时出现在乘法规则中。

你把加号和减号合并成一类，把乘号和除号合并成一类是可以的。把这4个运算符每个都单独作为一类，也是可以的。但是，不能把加号和乘号作为同一类，因为它们在算术运算中的优先级不同，肯定出现在不同的语法规则中。

我们再来回顾分析词法冲突的问题，即标识符和关键字的规则是有重叠的。Antlr是怎么解决这个问题的呢？很简单，它引入了优先级的概念。在Antlr的规则文件中，越是前面声明的规则，优先级越高。所以，我们把关键字的规则放在ID的规则前面。算法在执行的时候，会首先检查是否为关键字，然后才会检查是否为ID，也就是标识符。

这跟我们当时构造有限自动机做词法分析是一样的。那时，我们先判断是不是关键字，如果不是关键字，才识别为标识符。而在Antlr里，仅仅通过声明的顺序就解决了这个问题，省了很多事儿啊！

用Antlr生成语法分析器

已经知道如何用Antlr做一个词法分析器，还知道可以借鉴成熟的规则文件，让自己的词法规则文件变得更完善、更专业。接下来，试着用Antlr生成一个语法分析器，替代之前手写的语法分析器吧！

这一次的文件名叫做PlayScript.g4。PlayScript是为我们的脚本语言起的名称，文件开头是这样的：

grammar PlayScript;
import CommonLexer;   //导入词法定义

/*下面的内容加到所生成的Java源文件的头部，如包名称，import语句等。*/
@header {
package antlrtest;
}

然后把之前做过的语法定义放进去。Antlr内部有自动处理左递归的机制，你可以放心大胆地把语法规则写成下面的样子：

expression
    :   assignmentExpression
    |   expression ',' assignmentExpression
    ;

assignmentExpression
    :   additiveExpression
    |   Identifier assignmentOperator additiveExpression
    ;

assignmentOperator
    :   '='
    |   '*='
    |	'/='
    |   '%='
    |   '+='
    |   '-='
    ;

additiveExpression
    :   multiplicativeExpression
    |   additiveExpression '+' multiplicativeExpression
    |   additiveExpression '-' multiplicativeExpression
    ;

multiplicativeExpression
    :   primaryExpression
    |   multiplicativeExpression '*' primaryExpression
    |   multiplicativeExpression '/' primaryExpression
    |   multiplicativeExpression '%' primaryExpression
    ;

我们继续运行下面的命令，生成语法分析器：

antlr PlayScript.g4
javac antlrtest/*.java

然后测试一下生成的语法分析器：

grun antlrtest.PlayScript expression -gui

这个命令的意思是：测试PlayScript这个类的expression方法，也就是解析表达式的方法，结果用图形化界面显示。

我们在控制台界面中输入下面的内容：

age + 10 * 2  + 10
^D

其中^{D是按下Ctl键的同时按下D，相当于在终端输入一个EOF字符，即文件结束符号（Windows操作系统要使用}Z）。当然，你也可以提前把这些语句放到文件中，把文件名作为命令参数。之后，语法分析器会分析这些语法，并弹出一个窗口来显示AST：

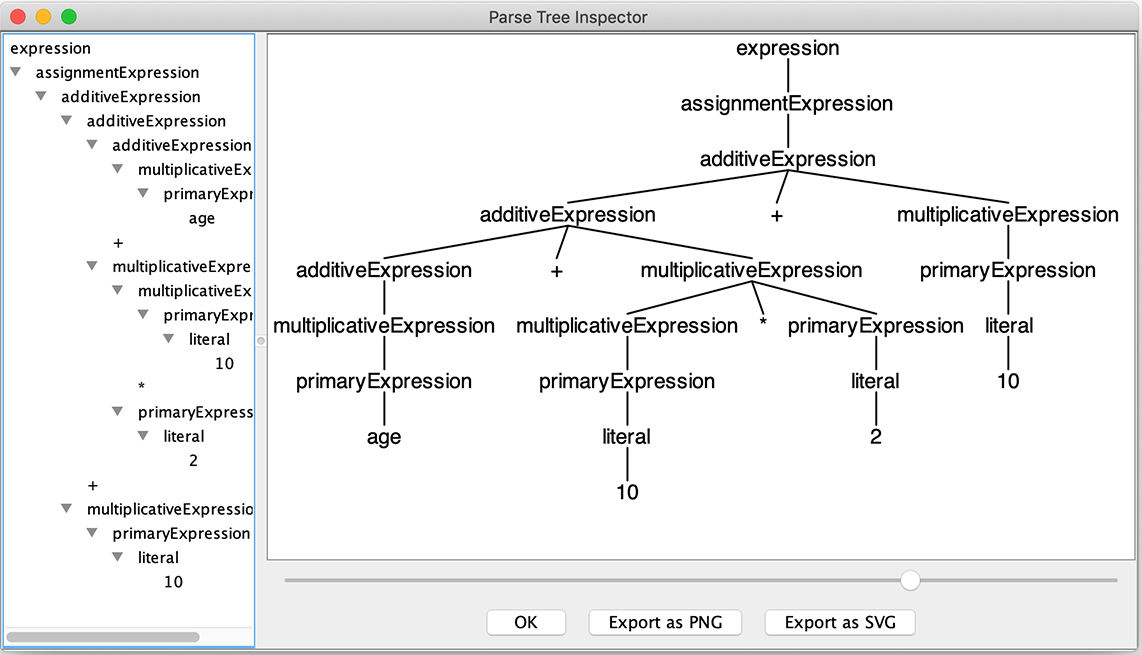
看得出来，AST完全正确，优先级和结合性也都没错。所以，Antlr生成的语法分析器还是很靠谱的。以后，你专注写语法规则就行了，可以把精力放在语言的设计和应用上。

总结

了解了Antlr，并用Antlr生成了词法分析器和语法分析器。有了工具的支持，你可以把主要的精力放在编写词法和语法规则上，提升了工作效率。

除此之外，我带你借鉴了成熟的词法规则和语法规则。你可以将这些规则用到自己的语言设计中。采用工具和借鉴成熟规则十分重要，站在别人的肩膀上能让自己更快成长。

用Antlr重构脚本语言

在词法方面，我们参考Java的词法规则文件，形成了一个CommonLexer.g4词法文件。在这个过程中，我们研究了更完善的字符串字面量的词法规则，还讲到要通过规则声明的前后顺序来解决优先级问题，比如关键字的规则一定要在标识符的前面。

目前来讲，我们已经完善了词法规则，所以今天我们来补充和完善一下语法规则，看一看怎样用最高效的速度，完善语法功能。比如一天之内，我们是否能为某个需要编译技术的项目实现一个可行性原型？

接下来，我们先把表达式的语法规则梳理一遍，让它达到成熟语言的级别，然后再把语句梳理一遍，包括前面几乎没有讲过的流程控制语句。最后再升级解释器，用Visitor模式实现对AST的访问，这样我们的代码会更清晰，更容易维护了。

完善表达式（Expression）的语法

我们可以把所有的运算都用一个语法规则来涵盖，然后用最简洁的方式支持表达式的优先级和结合性。在我建立的PlayScript.g4语法规则文件中，只用了一小段代码就将所有的表达式规则描述完了：

expression
    : primary
    | expression bop='.'
      ( IDENTIFIER
      | functionCall
      | THIS
      )
    | expression '[' expression ']'
    | functionCall
    | expression postfix=('++' | '--')
    | prefix=('+'|'-'|'++'|'--') expression
    | prefix=('~'|'!') expression
    | expression bop=('*'|'/'|'%') expression  
    | expression bop=('+'|'-') expression 
    | expression ('<' '<' | '>' '>' '>' | '>' '>') expression
    | expression bop=('<=' | '>=' | '>' | '<') expression
    | expression bop=INSTANCEOF typeType
    | expression bop=('==' | '!=') expression
    | expression bop='&' expression
    | expression bop='^' expression
    | expression bop='|' expression
    | expression bop='&&' expression
    | expression bop='||' expression
    | expression bop='?' expression ':' expression
    | <assoc=right> expression
      bop=('=' | '+=' | '-=' | '*=' | '/=' | '&=' | '|=' | '^=' | '>>=' | '>>>=' | '<<=' | '%=')
      expression
    ;

这个文件几乎包括了我们需要的所有的表达式规则，包括几乎没提到的点符号表达式、递增和递减表达式、数组表达式、位运算表达式规则等，已经很完善了。

那么它是怎样支持优先级的呢？原来，优先级是通过右侧不同产生式的顺序决定的。在标准的上下文无关文法中，产生式的顺序是无关的，但在具体的算法中，会按照确定的顺序来尝试各个产生式。

你不可能一会儿按这个顺序，一会儿按那个顺序。然而，同样的文法，按照不同的顺序来推导的时候，得到的AST可能是不同的。我们需要注意，这一点从文法理论的角度，是无法接受的，但从实践的角度，是可以接受的。比如LL文法和LR文法的概念，是指这个文法在LL算法或LR算法下是工作正常的。又比如我们之前做加法运算的那个文法，就是递归项放在右边的那个，在递归下降算法中会引起结合性的错误，但是如果用LR算法，就完全没有这个问题，生成的AST完全正确。

additiveExpression
    :   IntLiteral
    |   IntLiteral Plus additiveExpression
    ;

Antlr的这个语法实际上是把产生式的顺序赋予了额外的含义，用来表示优先级，提供给算法。所以，我们可以说这些文法是Antlr文法，因为是与Antlr的算法相匹配的。当然，这只是起的一个名字，方便你理解，免得你产生困扰。

我们再来看看Antlr是如何依据这个语法规则实现结合性的。在语法文件中，Antlr对于赋值表达式做了<assoc=right>的属性标注，说明赋值表达式是右结合的。如果不标注，就是左结合的，交给Antlr实现了！

我们不妨继续猜测一下Antlr内部的实现机制。我们已经分析了保证正确的结合性的算法，比如把递归转化成循环，然后在构造AST时，确定正确的父子节点关系。那么Antlr是不是也采用了这样的思路呢？或者说还有其他方法？你可以去看看Antlr生成的代码验证一下。

通过这个简化的算法，AST被成功简化，不再有加法节点、乘法节点等各种不同的节点，而是统一为表达式节点。你可能会问了：“如果都是同样的表达式节点，怎么在解析器里把它们区分开呢？怎么知道哪个节点是做加法运算或乘法运算呢？”

很简单，我们可以查找一下当前节点有没有某个运算符的Token。比如，如果出现了或者运算的Token（“||”），就是做逻辑或运算，而且语法里面的bop=、postfix=、prefix=这些属性，作为某些运算符Token的别名，也会成为表达式节点的属性。通过查询这些属性的值，你可以很快确定当前运算的类型。

到目前为止，我们彻底完成了表达式的语法工作，可以放心大胆地在脚本语言里使用各种表达式，把精力放在完善各类语句的语法工作上了。

完善各类语句（Statement）的语法

我先带你分析一下PlayScript.g4文件中语句的规则：

statement
    : blockLabel=block
    | IF parExpression statement (ELSE statement)?
    | FOR '(' forControl ')' statement
    | WHILE parExpression statement
    | DO statement WHILE parExpression ';'
    | SWITCH parExpression '{' switchBlockStatementGroup* switchLabel* '}'
    | RETURN expression? ';'
    | BREAK IDENTIFIER? ';'
    | SEMI
    | statementExpression=expression ';'
    ;

同表达式一样，一个statement规则就可以涵盖各类常用语句，包括if语句、for循环语句、while循环语句、switch语句、return语句等等。表达式后面加一个分号，也是一种语句，叫做表达式语句。

从语法分析的难度来看，上面这些语句的语法比表达式的语法简单的多，左递归、优先级和结合性的问题这里都没有出现。

1.研究一下if语句

在C和Java等语言中，if语句通常写成下面的样子：

if (condition)
  做一件事情;
else
  做另一件事情;

但更多情况下，if和else后面是花括号起止的一个语句块，比如：

if (condition){
  做一些事情；
}
else{
  做另一些事情；
}

它的语法规则是这样的：

statement : 
          ...
          | IF parExpression statement (ELSE statement)? 
          ...
          ;
parExpression : '(' expression ')';

我们用了IF和ELSE这两个关键字，也复用了已经定义好的语句规则和表达式规则。你看，语句规则和表达式规则一旦设计完毕，就可以被其他语法规则复用，多么省心！

但是if语句也有让人不省心的地方，比如会涉及到二义性文法问题。所以，接下来我们就借if语句，分析一下二义性文法这个现象。

2.解决二义性文法

学计算机语言的时候，提到if语句，会特别提一下嵌套if语句和悬挂else的情况，比如下面这段代码：

if (a > b)
if (c > d)
做一些事情；
else
做另外一些事情；

在上面的代码中，我故意取消了代码的缩进。那么，你能不能看出else是跟哪个if配对的呢？

一旦你语法规则写得不够好，就很可能形成二义性，也就是用同一个语法规则可以推导出两个不同的句子，或者说生成两个不同的AST。这种文法叫做二义性文法，比如下面这种写法：

stmt -> if expr stmt
      | if expr stmt else stmt
      | other

按照这个语法规则，先采用第一条产生式推导或先采用第二条产生式推导，会得到不同的AST。左边的这棵AST中，else跟第二个if配对；右边的这棵AST中，else跟第一个if配对。

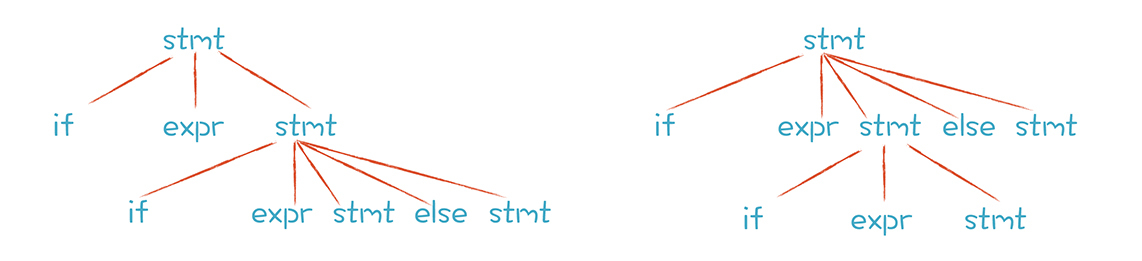
大多数高级语言在解析这个示例代码时都会产生第一个AST，即else跟最邻近的if配对，也就是下面这段带缩进的代码表达的意思：

if (a > b)
  if (c > d)
    做一些事情；
  else
    做另外一些事情；

那么，有没有办法把语法写成没有二义性的呢？当然有了。

stmt -> fullyMatchedStmt | partlyMatchedStmt
fullyMatchedStmt -> if expr fullyMatchedStmt else fullyMatchedStmt
                   | other
partlyMatchedStmt -> if expr stmt
                   | if expr fullyMatchedStmt else partlyMatchedStmt

按照上面的语法规则，只有唯一的推导方式，也只能生成唯一的AST：

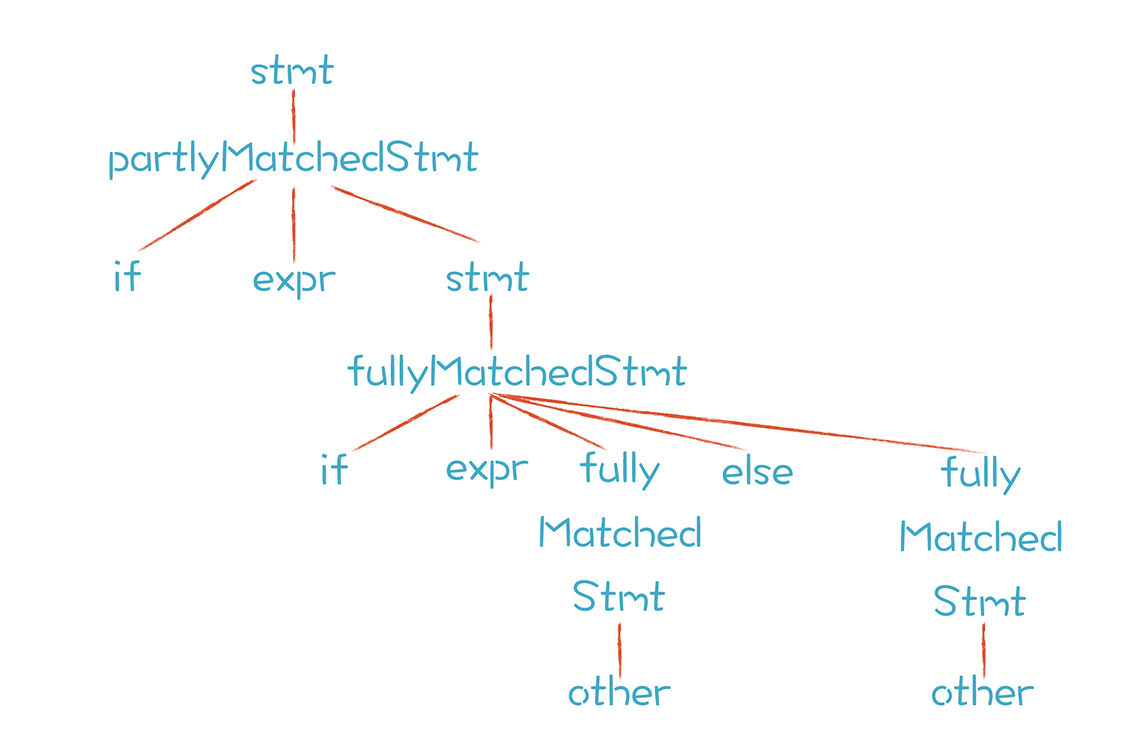
其中，解析第一个if语句时只能应用partlyMatchedStmt规则，解析第二个if语句时，只能适用fullyMatchedStmt规则。

这时，我们就知道可以通过改写语法规则来解决二义性文法。至于怎么改写规则，确实不像左递归那样有清晰的套路，但是可以多借鉴成熟的经验。

再说回我们给Antlr定义的语法，这个语法似乎并不复杂，怎么就能确保不出现二义性问题呢？因为Antlr解析语法时用到的是LL算法。

LL算法是一个深度优先的算法，所以在解析到第一个statement时，就会建立下一级的if节点，在下一级节点里会把else子句解析掉。如果Antlr不用LL算法，就会产生二义性。这再次验证了我们前面说的那个知识点：文法要经常和解析算法配合。

分析完if语句，并借它说明了二义性文法之后，我们再针对for语句做一个案例研究。

3.研究一下for语句

for语句一般写成下面的样子：

for (int i = 0; i < 10; i++){
  println(i);
}

相关的语法规则如下：

statement : 
         ...
          | FOR '(' forControl ')' statement
         ...
          ;

forControl 
          : forInit? ';' expression? ';' forUpdate=expressionList?
          ;

forInit 
          : variableDeclarators 
          | expressionList 
          ;

expressionList
          : expression (',' expression)*
          ;

从上面的语法规则中看到，for语句归根到底是由语句、表达式和变量声明构成的。代码中的for语句，解析后形成的AST如下：

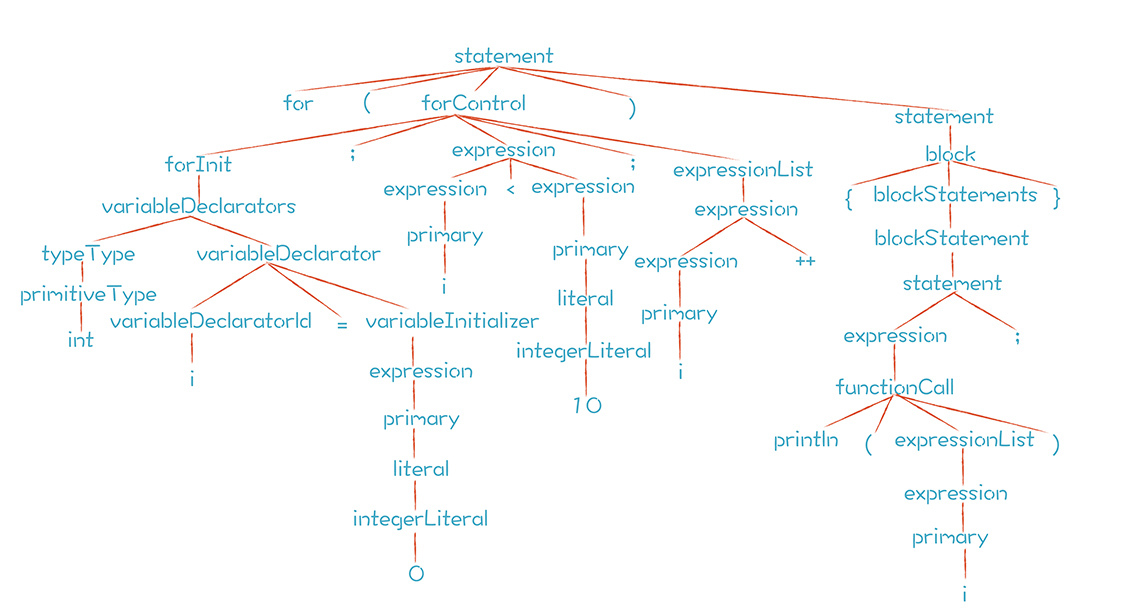
熟悉了for语句的语法之后，我想提一下语句块（block）。在if语句和for语句中，会用到它，所以我捎带着把语句块的语法构成写了一下，供你参考：

block
    : '{' blockStatements '}'
    ;

blockStatements
    : blockStatement*
    ;

blockStatement
    : variableDeclarators ';'     //变量声明
    | statement
    | functionDeclaration         //函数声明
    | classDeclaration            //类声明
    ;

现在，我们已经拥有了一个相当不错的语法体系，除了要放到后面去讲的函数、类有关的语法之外，我们几乎完成了playscript的所有的语法设计工作。接下来，我们再升级一下脚本解释器，让它能够支持更多的语法，同时通过使用Visitor模式，让代码结构更加完善。

用Vistor模式升级脚本解释器

我们在纯手工编写的脚本语言解释器里，用了一个evaluate()方法自上而下地遍历了整棵树。随着要处理的语法越来越多，这个方法的代码量会越来越大，不便于维护。而Visitor设计模式针对每一种AST节点，都会有一个单独的方法来负责处理，能够让代码更清晰，也更便于维护。

Antlr能帮我们生成一个Visitor处理模式的框架，我们在命令行输入：

antlr -visitor PlayScript.g4

-visitor参数告诉Antlr生成下面两个接口和类：

public interface PlayScriptVisitor<T> extends ParseTreeVisitor<T> {...}

public class PlayScriptBaseVisitor<T> extends AbstractParseTreeVisitor<T> implements PlayScriptVisitor<T> {...}

在PlayScriptBaseVisitor中，可以看到很多visitXXX()这样的方法，每一种AST节点都对应一个方法，例如：

@Override 
public T visitPrimitiveType(PlayScriptParser.PrimitiveTypeContext ctx) {...}

其中泛型< T >指的是访问每个节点时返回的数据的类型。在我们手工编写的版本里，当时只处理整数，所以返回值一律用Integer，现在我们实现的版本要高级一点，AST节点可能返回各种类型的数据，比如：

• 浮点型运算的时候，会返回浮点数；
• 字符类型运算的时候，会返回字符型数据；
• 还可能是程序员自己设计的类型，如某个类的实例。

所以，我们就让Visitor统一返回Object类型好了，能够适用于各种情况。这样，我们的Visitor就是下面的样子（泛型采用了Object）：

public class MyVisitor extends PlayScriptBaseVisitor<Object>{
  ...
}

这样，在visitExpression()方法中，我们可以编写各种表达式求值的代码，比如，加法和减法运算的代码如下：

public Object visitExpression(ExpressionContext ctx) {
        Object rtn = null;
        //二元表达式
        if (ctx.bop != null && ctx.expression().size() >= 2) {
            Object left = visitExpression(ctx.expression(0));
            Object right = visitExpression(ctx.expression(1));
            ...
            Type type = cr.node2Type.get(ctx);//数据类型是语义分析的成果

            switch (ctx.bop.getType()) {
            case PlayScriptParser.ADD:        //加法运算
                rtn = add(leftObject, rightObject, type);
                break;
            case PlayScriptParser.SUB:        //减法运算
                rtn = minus(leftObject, rightObject, type);
                break;
            ...   
            }
        }
        ...
}

其中ExpressionContext就是AST中表达式的节点，叫做Context，意思是你能从中取出这个节点所有的上下文信息，包括父节点、子节点等。其中，每个子节点的名称跟语法中的名称是一致的，比如加减法语法规则是下面这样：

expression bop=('+'|'-') expression 

那么我们可以用ExpressionContext的这些方法访问子节点：

ctx.expression();     //返回一个列表，里面有两个成员，分别是左右两边的子节点
ctx.expression(0);    //运算符左边的表达式，是另一个ExpressionContext对象
ctx.expression(1);    //云算法右边的表达式
ctx.bop();            //一个Token对象，其类型是PlayScriptParser.ADD或SUB
ctx.ADD();            //访问ADD终结符，当做加法运算的时候，该方法返回非空值
ctx.MINUS()；         //访问MINUS终结符

在做加法运算的时候我们还可以递归的对下级节点求值，就像代码里的visitExpression(ctx.expression(0))。同样，要想运行整个脚本，我们只需要visit根节点就行了。

所以，我们可以用这样的方式，为每个AST节点实现一个visit方法。从而把整个解释器升级一遍。除了实现表达式求值，我们还可以为今天设计的if语句、for语句来编写求值逻辑。以for语句为例，代码如下：

// 初始化部分执行一次
if (forControl.forInit() != null) {
    rtn = visitForInit(forControl.forInit());
}

while (true) {
    Boolean condition = true; // 如果没有条件判断部分，意味着一直循环
    if (forControl.expression() != null) {
        condition = (Boolean) visitExpression(forControl.expression());
    }

    if (condition) {
        // 执行for的语句体
        rtn = visitStatement(ctx.statement(0));

        // 执行forUpdate，通常是“i++”这样的语句。这个执行顺序不能出错。
        if (forControl.forUpdate != null) {
            visitExpressionList(forControl.forUpdate);
        }
    } else {
        break;
    }
}

你需要注意for语句中各个部分的执行规则，比如：

• forInit部分只能执行一次；
• 每次循环都要执行一次forControl，看看是否继续循环；
• 接着执行for语句中的语句体；
• 最后执行forUpdate部分，通常是一些“i++”这样的语句。

支持了这些流程控制语句以后，我们的脚本语言就更丰富了！

总结

用Antlr高效地完成了很多语法分析工作，比如完善表达式体系，完善语句体系。除此之外，我们还升级了脚本解释器，使它能够执行更多的表达式和语句。

在实际工作中，针对面临的具体问题，我们完全可以像今天这样迅速地建立可以运行的代码，专注于解决领域问题，快速发挥编译技术的威力。

而且在使用工具时，针对工具的某个特性，比如对优先级和结合性的支持，我们大致能够猜到工具内部的实现机制，因为我们已经了解了相关原理。