单调栈
- 单调递增栈:数据出栈的序列为单调递增序列(比站内元素小就入栈,否则将栈中比当前元素小的元素弹出后再入栈)
- 单调递减栈:数据出栈的序列为单调递减序列(比站内元素大就入栈,否则将栈中比当前元素大的元素弹出后再入栈)
视野总和
描叙:有n个人站队,所有的人全部向右看,个子高的可以看到个子低的发型,给出每个人的身高,问所有人能看到其他人发现总和是多少。
输入:4 3 7 1
输出:2
思路:设置一个单调递增栈,当这个人可以被站内人看到时(即比栈内数小时)入栈,同时将栈内每个人能看到的人数加一,如果遇到了一个比栈顶元素高的人,那么栈内一些人是看不到他的,所以将这些看不到他的人出栈,出栈完成后再将栈内剩下元素能看到的人数各自加一。大致是这种思路,但是由于这题求得是总和,所以不必求出每个人能看到多少人,避免每次有元素入栈都要遍历原有栈内的元素。可以改为在每个元素出栈时计算他能看到的人数。例如第i个人要入栈(即第i个人比s.top()这个人高时),此时栈内s.top()这个人被第i个人挡住了,第i个人后面的都看不到了,所以其出栈时看到的人数为i~s.top()之间的人。
#include<bits/stdc++.h>
using namespace std;
int FieldSum(vector<int>& v)
{
int sum=0;
v.push_back(INT_MAX);
stack<int> s;
for(int i=0;i<v.size();i++)
{
while(!s.empty()&&v[i]>v[s.top()])
{
int x=s.top();
s.pop();
sum+=(i-x-1); //i为当前元素,x为出栈元素,相减部分为x可以看到的数量;
}
s.push(i);
}
return sum;
}
int main()
{
int a[6]={8,3,2,7,1,4};
vector<int> v;
for(int i=0;i<6;i++)
{
v.push_back(a[i]);
}
cout<<FieldSum(v)<<endl;
return 0;
}
柱状图中最大
描述
Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1,
find the area of largest rectangle in the histogram.
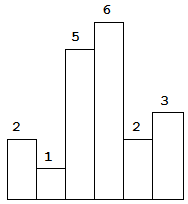
图 4-1 Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].
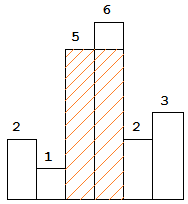
图 4-2 The largest rectangle is shown in the shaded area, which has area = 10 unit.
For example, Given height = [2,1,5,6,2,3], return 10.
单调栈
理解:当遍历到第i个数时,会算出所有向左看时在数i前即包含第(i-1)个数的最大值,假设这个最大值矩形左边边界为left,右边为right(即此时right+1大于left-1),这种情况下,以左边界[left]>[right+1]但是[left-1]<[right+1],所以 这里的大小关系也是出栈的依据,以此来计算宽度,h[right]即为这一段上的最小值。
#include<bits/stdc++.h>
using namespace std;
//#define MAX 10005
int largestRectangleArea(vector<int>& heights)
{
stack<int> s;
int max=0;
heights.push_back(0); //用于处理最后一个数据
int len=heights.size();
for(int i=0;i<len;i++)
{
while(!s.empty()&&heights[s.top()]>heights[i])
{
int x=s.top();
s.pop();
//temp为宽度,如果s为空,则说明,x之前的元素都比x高,所以均可计入,宽度即为(i-1-0+1)
//s为空时,两边的边界依次为下标为0,下标为i-1;
int temp=heights[x]*(s.empty()?i:(i-s.top()-1));
max=max>temp?max:temp;
}
s.push(i);
}
return max;
}
int main()
{
int a[6]={2,1,5,6,2,3};
vector<int> v;
for(int i=0;i<6;i++)
{
v.push_back(a[i]);
}
cout<<largestRectangleArea(v)<<endl;
return 0;
}
分治法
此题还可以使用分治法,记左右边界为left,right,可以先找出一个序列中的最小值min,若最大矩形包含这个min,则最大矩形一定为(right-left+1)*min;所以可以分为(left,min-1),(min+1,right)两个子问题寻找最大矩形,然后三种情况取最大值。(因为最大矩形连续,而第二三种情况一定不包含min,所以可以分开看成两个无联系的子问题)
int maxArea(int left,int right,vector<int>& v)
{
if(left==right)
return v[left];
bool sortedlr=true; //是否从左到右递增
bool sortedrl=true; //是否从右到左递增
int min=left;
for(int i=left;i<=right;i++)
{
if(v[i]>v[i-1])
{
sortedrl=false;
}
if(v[i]<v[i-1])
{
sortedlr=false;
}
if(v[i]<v[min])
{
min=i;
}
}
if(sortedlr)
{
int maxa=v[left]*(right-left+1);
for(int i=left+1;i<=right;i++)
{
int temp=v[i]*(right-i+1);
maxa=maxa>temp?maxa:temp;
}
return maxa;
}
if(sortedrl)
{
int maxa=v[right]*(right-left+1);
for(int i=right-1;i>=left;i--)
{
int temp=v[i]*(i-left+1);
maxa=maxa>temp?maxa:temp;
}
return maxa;
}
else
{
//继续分治
int l=0;
if(left<min)
{
l=maxArea(left,min-1,v);
}
int r=0;
if(right>min)
{
r=maxArea(min+1,right,v);
}
int x=l>r?l:r;
int temp=v[min]*(right-left+1);
return x>temp?x:temp;
}
}
int largestRectangleArea(vector<int>& heights)
{
int left=0;
int right=heights.size()-1;
if(right==-1)
return 0;
else if(right==0)
{
return heights[0];
}
else
{
return maxArea(left,right,heights);
}
}
求最大区间
描述:给出一组数字,求一区间,使得区间元素和乘以区间最小值最大,结果要求给出这个最大值和区间的左右端点
输入:3 1 6 4 5 2
输出:60
3 5
解释:将3到5(6+4+5)这段区间相加,将和与区间内最小元素相乘获得最大数字60
思路:使用暴力解法求出所有区间,再求出区间的最小值相乘跟新数据,并不是一种很好的算法,所以经过上面俩题的磨炼,此时我们应该使用一个单调递减栈同矩形相似,如果以一个数为该区间最小值,则算出该最小值可以构成的最大区间。
#include<bits/stdc++.h>
using namespace std;
int findMax(vector<int>& v,int &p,int &q)
{
v.push_back(0);
stack<int> s;
int max=0;
int sum;
for(int i=0;i<v.size();i++)
{
while(!s.empty()&&v[s.top()]>v[i])
{
int x=s.top();
s.pop();
sum=0;
int j;
if(s.empty())
{
//p=0;
j=0;
}
else
{
//p=s.top()+1;
j=s.top()+1;
}
for(j;j<i;j++)
{
sum+=v[j];
}
int temp=sum*v[x];
max=max>temp?max:temp;
if(max==temp)
{
p=s.empty()?0:s.top()+1;
q=i-1;
}
}
s.push(i);
}
return max;
}
int main()
{
int a[]={3,1,6,4,5,2};
vector<int> v;
int p,q;
for(int i=0;i<6;i++)
{
v.push_back(a[i]);
}
int x=findMax(v,p,q);
cout<<x<<endl;
cout<<(p+1)<<" "<<(q+1)<<endl; //p,q,为下标,输出为序号
return 0;
}
寻找无序数组每个元素的后面第一个比它大的元素值
如题
#include<bits/stdc++.h>
using namespace std;
vector<int> nextmax(vector<int> &v)
{
stack<int> s;
vector<int> res(v.size());
int size=v.size();
int i=0;
while(i<size)
{
if(s.empty()||v[s.top()]>=v[i])
{
s.push(i++);
}
else
{
int tmp=s.top();
res[tmp]=v[i];
s.pop();
}
}
while(!s.empty())
{
res[s.top()]=INT_MAX; //将后面没有比他更大的元素置为INT_MAXINT_MAX
s.pop();
}
return res;
}
int main()
{
int a[10]={1,2,4,2,5,76,89,3,45,34};
vector<int> v;
for(int i=0;i<10;i++)
{
v.push_back(a[i]);
}
vector<int> res=nextmax(v);
for(int i=0;i<res.size();i++)
{
cout<<res[i]<<endl;
}
return 0;
}