题解:
首先观察到题目要求的是合法回文串的个数,而回文串要求从前往后和从后往前是一样的,因此我们假设有两只猪,分别从左上和右下开始走,走相同的步数最后相遇,那么它们走的路能拼在一起构成一个回文串,当且仅当它们走字符串是完全相同的。
那么我们可以根据这个性质进行DP,设f[i][j][k][l]表示第一只猪走到(i, j),第二只猪走到(k, l)的方案数。
那么观察到$i + j = k + l$,所以$l$是没必要记录的,因为前面三个确定,l就确定了,然后因为i从1 开始枚举,每次只能走一步,所以只会用到上一步的方案,所以可以滚动一下,这样时空复杂度就都可以承受了。
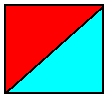
因为要限制两只猪走的步数一样,注意限制第一只猪在红色的三角形中,另一只猪在蓝色的三角形中。

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define R register int 4 #define AC 510 5 #define mod 1000000007 6 #define LL long long 7 8 int n, m; 9 LL f[2][AC][AC], ans; 10 char s[AC][AC]; 11 12 void pre() 13 { 14 scanf("%d%d", &n, &m); 15 for(R i = 1; i <= n; i ++) scanf("%s", s[i] + 1); 16 if(s[1][1] != s[n][m]) {printf("0 "); exit(0);} 17 } 18 19 inline bool check(int i, int j, int k, int l) 20 { 21 if(i == k && j == l) return true; 22 else if(i + 1 == k && j == l) return true; 23 else if(i == k && j + 1 == l) return true; 24 return false; 25 } 26 27 void work() 28 { 29 int l, now = 1, b = (n + m) / 2; 30 f[1][1][n] = 1; 31 for(R i = 1; i <= n; i ++, now ^= 1) 32 { 33 for(R j = 1; j + i - 1 <= b; j ++) 34 { 35 if(i == 1 && j == 1) continue; 36 for(R k = n; k >= i; k --) 37 { 38 l = n + m + 2 - i - j - k; 39 if(l < j || l > m) continue; 40 if(s[i][j] != s[k][l]) continue; 41 f[now][j][k] = f[now ^ 1][j][k] + f[now ^ 1][j][k + 1]; 42 f[now][j][k] += f[now][j - 1][k] + f[now][j - 1][k + 1]; 43 f[now][j][k] %= mod; 44 if(check(i, j, k, l)) ans += f[now][j][k]; 45 if(ans > mod) ans -= mod; 46 } 47 } 48 memset(f[now ^ 1], 0, sizeof(f[now ^ 1]));//因为有同层转移,所以要memset,而不能枚举到它的时候再重置 49 } 50 printf("%lld ", ans); 51 } 52 53 void work1() 54 { 55 int l, now = 1, b = (n + m) / 2; 56 f[1][1][n] = 1; 57 for(R i = 1; i <= n; i ++, now ^= 1) 58 { 59 for(R j = 1; j + i - 1 <= b; j ++) 60 { 61 if(i == 1 && j == 1) continue; 62 for(R k = n; k >= i; k --) 63 { 64 l = n + m + 2 - i - j - k; 65 if(l < j || l > m) continue; 66 if(s[i][j] != s[k][l]) continue; 67 f[i][j][k] += f[i - 1][j][k] + f[i - 1][j][k + 1]; 68 f[i][j][k] += f[i][j - 1][k] + f[i][j - 1][k + 1]; 69 f[i][j][k] %= mod; 70 if(check(i, j, k, l)) ans += f[i][j][k]; 71 if(ans > mod) ans -= mod; 72 } 73 } 74 } 75 printf("%lld ", ans); 76 } 77 78 int main() 79 { 80 // freopen("in.in", "r", stdin); 81 pre(); 82 work(); 83 // fclose(stdin); 84 return 0; 85 }
