st表是一种基于倍增思想的DP。
用于求一个数列中的某个区间的最大/最小值。
用st[i][j]表示从第i个开始往后2^j个点,最大的是多少。
我们令k[i]表示2^i等于多少
那么有转移方程
st[i][j] = max(st[i][j - 1], st[i + k[i - 1]][j - 1]);
为什么呢?
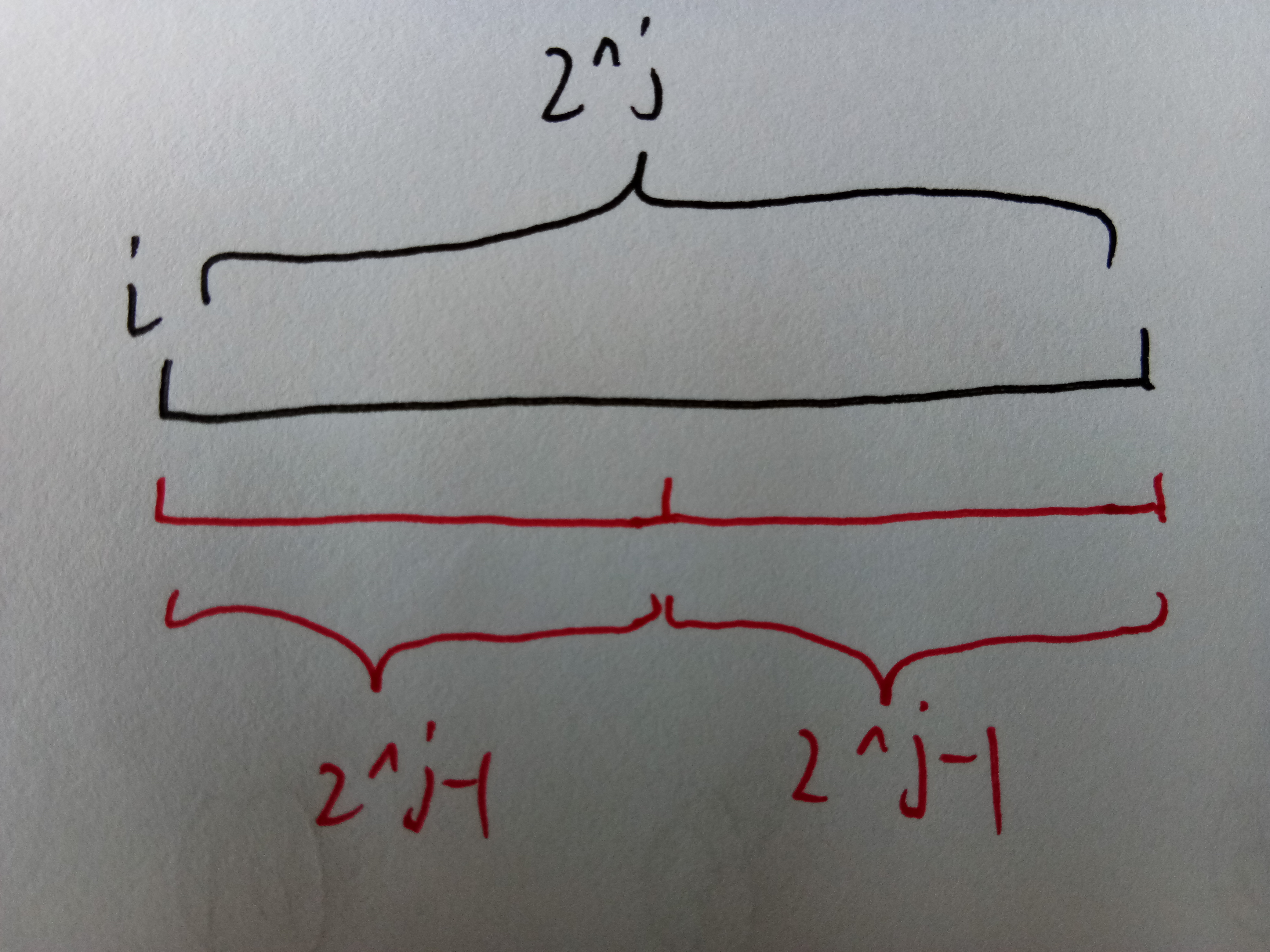
例如这幅图,显然黑色块的答案可以由合并下面两块得到。
那如果查询的时候不是2的整次幂怎么办?
这其实是没有问题的,你可以观察下图……
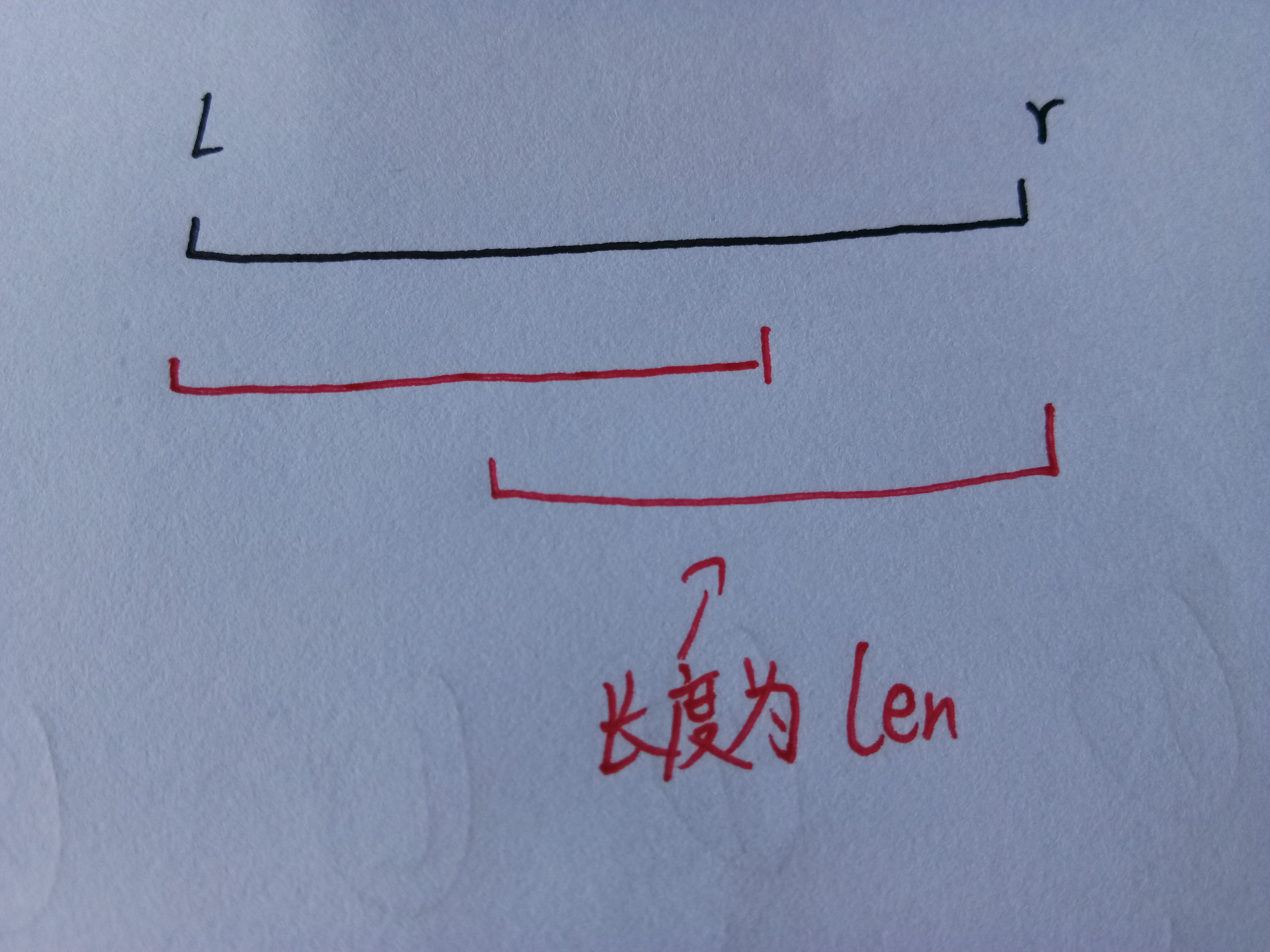
因为小区间有重叠部分并不影响,因此完全可以用稍大一点的小区间凑出大区间。
预处理一点信息以快速查询答案即可。
(早期代码,没有空格空行,略丑)
1 #include<bits/stdc++.h> 2 using namespace std; 3 int n,m,s[100500],f[100500][18],p[100500]; 4 int Max(int a,int b) 5 { 6 if(a>b)return a; 7 else return b; 8 } 9 int Min(int a,int b) 10 { 11 if(a<b)return a; 12 else return b; 13 } 14 void pre() 15 { 16 int i,a,key=1; 17 for(i=1;i<=n;i++) 18 { 19 if(i==(key<<1))p[i]=p[i-1]+1,key<<=1; 20 else p[i]=p[i-1]; 21 scanf("%d",&a); 22 f[i][0]=a; 23 } 24 for(int j=1;j<=17;j++) 25 for(i=1;i<=n;i++) 26 { 27 f[i][j]=Max(f[i][j-1],f[Min(i+(1<<(j-1)),n)][j-1]); 28 } 29 } 30 int main() 31 { 32 int i,a,b,k; 33 scanf("%d%d",&n,&m); 34 pre(); 35 for(i=1;i<=m;i++) 36 { 37 scanf("%d%d",&a,&b); 38 k=p[b-a+1]; 39 printf("%d ",Max(f[a][k],f[b-(1<<k)+1][k])); 40 } 41 return 0; 42 }