复习一下,,,
刚开始学树链剖分的时候想了好久都没明白。
实际上树链剖分也不是什么很高大上的东西,懂了还是很简单的。
其实这就是一个对树进行遍历并编号的过程。
同时为了方便(跟复杂度相关?),每次都优先选择重儿子进行编号。
接下来就是具体过程了。
首先是一些概念:
1,重儿子
我们令点x的所有儿子中,Size最大的点为它的重儿子。
2,重链
我们从一个点沿着重儿子向下遍历,所遍历到的链称为重链。
(我们从点x向下遍历时,点x属于从它向下遍历到的重链,且为链首)
3,轻链
我们从x向下遍历时,除了重链,其他链对于x都是轻链(因为是轻儿子开头)
4,Size
一个节点(包括自己)的子树大小。
5,top
每个点的链首。
因为我们是在dfs遍历整棵树,重儿子只是改变了我们遍历的顺序,因此显然每个点只会被遍历一次,因此每个点也将属于且仅属于一条链
画个图吧。
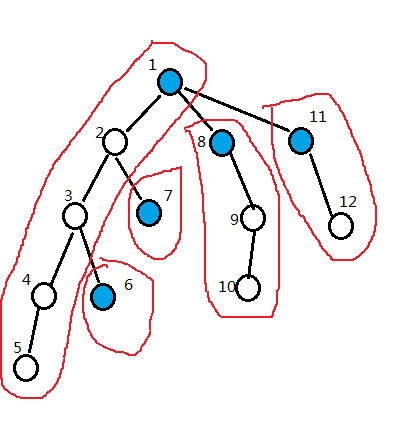
每个红圈都是一条链,蓝色节点则为链首。
那么根据这样的编号方式我们可以发现什么规律呢?
1,每条链中的点的编号是连续的。
比如最长的那条链,编号依次为1, 2, 3, 4, 5。
原因很显然,因为我们编号时是先走的重儿子,因此一条链的形成是一次性遍历到的,中途没有任何拐弯。
2,每棵子树中的点的编号是连续的。
这个原因也很好理解,因为我们虽然优先走了重儿子,但本质上还是一个dfs遍历的过程,所以子树内编号当然是连续的了。
这样分完有什么用呢?
可以将树上的问题转化为链上的问题。
比如如果要修改6 ~ 10 的路径,如果不用树链剖分的话我们就需要获取t = LCA(6, 10),然后分别从6和10开始往上跑,O(n)的修改路径上的权值,这显然是不够优的。
如果我们使用树链剖分的话,我们就可以把这个问题转化为修改6, 3 --- > 1, 10 --->8了。而3 ---> 1 = 3 ---> 2 ---> 1, 10 ---> 8 = 10 ---> 9 ---> 8,因为中间编号都是连续的,
所以如果我们知道了端点,就知道了我们要修改哪些点,所以就可以直接用线段树来维护了。这样就只用O(logn)的修改了。
而具体修改方法应该是像倍增找LCA哪样两个点同时跳,免得错过了LCA,其实原理和倍增是一样的,只不过倍增跳的比较有规律一点,而树链剖分就是杂乱无章的跳了。。。
但是如果遇到一个很长的链,一下子就可以上去了,而这个几率还是很高的,因此树链剖分的效率是很高的。
当然也不一定要用线段树来维护,因为树链剖分的作用只是将树给剖成几条链而已。转化为序列上的问题后想怎么维护自然是怎么维护了
下面是luogu树链剖分模板,不过由于本人代码及其冗长。。。(但自认为还是很清晰的)而且这个是早期代码,所以可能会有一些奇怪的变量名。。。

#include<bits/stdc++.h> using namespace std; #define Rint register int #define AC 200200 //~~~~~~~~~~~~~~~~~~~~~ #define ACway 420040 #define D printf("line in %d ",__LINE__); int n,m,mod,root,change; int tot,date[ACway],Next[ACway],Head[AC]; int top[AC],power[AC],size[AC],deep[AC],repower[AC],cnt,son[AC],father[AC],id[AC]; int tree[ACway],l[ACway],r[ACway],lazy[ACway],ans,addnum; inline int read() { int x=0,k=1;char c; while(isspace(c=getchar())); if(c=='-')k=-1,c=getchar(); while(c>='0' && c<='9')x=x*10+c-'0',c=getchar(); return x*k; } inline void add(int f,int w)//加双向边 { date[++tot]=w , Next[tot]=Head[f] , Head[f]=tot; date[++tot]=f , Next[tot]=Head[w] , Head[w]=tot; } inline void pre() { int a,b; n=read() , m=read() , root=read() , mod=read(); for(int i=1; i<=n ;i++) power[i]=read(); for(Rint i=1; i<=n-1 ;i++) { a=read(),b=read(); add(a,b); } } void dfs1(int x, int fa, int dep)//求出size && 重儿子 && 深度 { int maxson=-1,now; deep[x]=dep; father[x]=fa; size[x]=1;//size初始值为1 for(Rint i=Head[x]; i ;i=Next[i]) { now=date[i]; if(now!=fa)//不是父亲,即为儿子 { dfs1(now,x,dep+1);//先求出儿子的size size[x]+=size[now];//加上儿子的size if(size[now] > maxson) maxson=size[now],son[x]=now;//寻找重儿子 } } } void dfs2(int x, int topx)//编号 && 当前所在链的链首 { int now; id[x]=++cnt;//按优先重儿子的DFS序为节点重新编号 repower[cnt]=power[x];//直接放到树上 top[x]=topx; if(!son[x])return ;//如果没有儿子了就返回 dfs2(son[x],topx);//由于是重儿子,所以top是要继承下去的 for(Rint i=Head[x]; i ;i=Next[i]) { now=date[i]; if(father[x]==now || now==son[x])continue;//跳过重儿子和父亲 dfs2(now,now);//新开一条链 } } void built(int x,int ll,int rr)//建树 { int mid=(ll+rr)/2; l[x]=ll,r[x]=rr; if(ll==rr) { tree[x]=repower[ll]; return ; } else { built(x*2,ll,mid); built(x*2+1,mid+1,rr); tree[x]=tree[x*2]+tree[x*2+1]; } } void search(int x,int ll,int rr)//线段树的区间查询 { int mid=(l[x]+r[x])/2;//mid是属于左儿子的,mid+1属于右儿子 if(lazy[x])//下传标记 { if(l[x]==r[x]) { tree[x]+=lazy[x]; ans+=tree[x]; if(ans>mod)ans%=mod;//error!!!这里也改变了ans,所以也要取模 lazy[x]=0;//error!!!!!!! return ;//如果是叶子节点,直接返回 } tree[x]=(tree[x]+(lazy[x]*(r[x]-l[x]+1))%mod)%mod;//因为是区间和 lazy[x*2]+=lazy[x];//不能直接等于,因为可能儿子的lazy里面是有数的,不能覆盖了 lazy[x*2+1]+=lazy[x]; lazy[x]=0; } if(l[x]==ll && r[x]==rr) { ans+=tree[x]; if(ans>mod)ans%=mod;//如果找到当前查询区间,那么加入ans return ; } else if(mid>=rr) search(x*2,ll,rr);//如果这个区间在左边,去左儿子 else if(mid+1<=ll) search(x*2+1,ll,rr); else //不然就两边都有 { search(x*2,ll,mid); search(x*2+1,mid+1,rr); } } void adddate(int x,int ll,int rr)//区间修改 { int mid=(l[x]+r[x])/2; if(l[x]==ll && r[x]==rr)//如果区间完全吻合,打上标记 { lazy[x]+=addnum; return; } else tree[x]=(tree[x]+(rr-ll+1)*addnum) % mod;//不然就直接更新值 error!!!! if(mid>=rr) adddate(x*2,ll,rr); else if(mid+1<=ll) adddate(x*2+1,ll,rr); else { adddate(x*2,ll,mid); adddate(x*2+1,mid+1,rr); } } inline void getans1(int x,int y) { int ans1=0; while(top[x]!=top[y])//不在同一条链上error!!!啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊while啊啊啊啊啊啊啊啊 { if(deep[top[x]]<deep[top[y]])swap(x,y); ans=0; search(1,id[top[x]],id[x]); ans1+=ans; ans1%=mod; x=father[top[x]]; } if(deep[x]>deep[y])swap(x,y);//x换成深度浅的 ans=0; search(1,id[x],id[y]); ans1+=ans; printf("%d ",ans1%mod); } void changetree(int x,int y) { addnum%=mod; while(top[x]!=top[y]) { if(deep[top[x]] < deep[top[y]])swap(x,y); adddate(1,id[top[x]],id[x]); x=father[top[x]]; } if(deep[x]<deep[y])adddate(1,id[x],id[y]); else adddate(1,id[y],id[x]); } inline void work() { int a,b; for(Rint i=1; i<=m ;i++) { a=read(); if(a==1)//修改 { a=read(),b=read(),addnum=read(); changetree(a,b); } else if(a==2)//查询路径上的区间和 { a=read(),b=read(); getans1(a,b); } else if(a==3) { a=read(),addnum=read(); addnum%=mod; adddate(1,id[a],id[a]+size[a]-1); } else { a=read(); ans=0; search(1,id[a],id[a]+size[a]-1); printf("%d ",ans%mod);//error!!!在这里取个mod保险啊 } } } int main() { // freopen("in.in","r",stdin); pre(); dfs1(root,0,1); dfs2(root,root); built(1,1,size[root]); work(); // fclose(stdin); return 0; }
