如果学不会也不要打我。
假设你会线段树
开始!
主席树也叫可持久化线段树
顾名思义,它能够保存线段树在每个时刻的版本。
什么叫每个时刻的版本?你可能对一棵普通线段树进行各种修改,这每种样子就是我们所说的不同时刻的版本。
假设我们对线段树进行单点修改,维护区间和。
每次修改操作中,只有logn个节点会被修改,我们可以复制这些被修改的节点,而不复制没有被改变的节点(以提高效率)。
最后通过特殊的方式建立出新时刻的树。
建造方式如下:
假设上一时刻的树长这样:
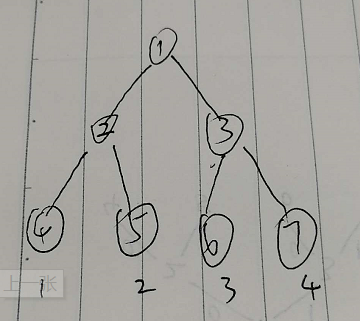
现在进行修改操作,对下标为3的位置修改,也就是说修改1 3 6号节点。若是普通线段树,则直接修改1 3 6三个节点。但是在主席树中,我们不直接在1 3 6号节点上修改。而是新建3个节点,分别对应1 3 6号节点,对新建节点进行本想在1 3 6号节点进行的操作(“本想”指普通线段树)。
如图:
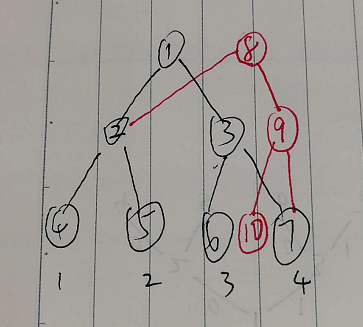
关于不同版本的线段树理解
接上图,可以观察到,1号和8号往下分别是两棵不同版本的线段树,不同版本共用很多节点。这并不会影响自上而下的查询。
单点修改的例子

以下内容质量不高:
寒羽吾:
用主席树做kth number,就是在空线段树的基础上,依次在线段树的位置a[1]处加一,a[2]处加一。即用线段树维护值在某区间中的ai有多少个。然后可以在线段树上移动指针,找到第k个。
寒羽吾:
考虑区间[l,r]的限制,即r时刻的线段树减去l-1时刻的线段树,就得到维护ai(下标i在[l,r]中)的线段树了。
寒羽吾:
查询的时候不必真把做差得到的线段树求出来,需要这个线段树的什么位置就访问r版本和l-1版本的对应点,取出值相减即可。
寒羽吾:
上面是我写的板子,t表示树节点,w[0]左孩子w[1]右孩子。
寒羽吾:
理论上维护21e9个元素的线段树是开不下节点的(也是时间上不可建立的),但因为主席树的特殊性:只建立需要用(改变)的节点。所以可以不对ai进行离散化,直接建立“看似”能维护21e9个元素的线段树。
#include<bits/stdc++.h>
using namespace std;
struct node{
int sum;
int w[2];
}t[5000005];
int np;
int n,m;
int st[100005];
int a[100005];
void plu(int x,int c,int num){
int now=++np;
t[now]=t[x];
if(c<0){
t[now].sum++;
return;
}
int p=(num>>c)&1;
plu(t[now].w[p],c-1,num);
t[now].w[p]=now+1;
t[now].sum=t[t[now].w[0]].sum+t[t[now].w[1]].sum;
}
int solve(int l,int r,int k){
int lx=st[l-1],rx=st[r],ans=0;
for(int i=0;i<=30;i++){
int p=0;
if(t[t[rx].w[0]].sum-t[t[lx].w[0]].sum<k)
k-=t[t[rx].w[0]].sum-t[t[lx].w[0]].sum,
p=1;
lx=t[lx].w[p],
rx=t[rx].w[p],
ans=ans<<1|p;
}
return ans;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
a[i]+=1e9;
}
np=1;st[0]=1;
for(int i=1;i<=n;i++){
st[i]=np+1;
plu(st[i-1],30,a[i]);
}
for(int i=1;i<=m;i++){
int l,r,k;
scanf("%d%d%d",&l,&r,&k);
printf("%d
",int(solve(l,r,k)-1e9));
}
return 0;
}