午后的阳光,那么灿烂,如果不是温度过高,那么去西湖看看风景还是不错的。想着,现在西湖边应该是平静的湖面,加上无数知了在柳枝上演奏着交响曲吧。小看了下非诚勿扰,那男生为了女孩唐静付出了7年,唉,可是他错了,女孩根本不爱他,不过期间他的执着和付出,很让我感动,也许自己不太像他那样,才会让自己有现在的处境吧。也许吧。小感慨下。不过现在也挺好的,上上班,写写文章,然后天气凉快点还可以到处玩,杭州是个旅游休闲的好地方啊。扯远了,吃了饭回来,还是有些小感触啊。
回归正题,既然二分法讲完了,那么继续三分法吧。二分法适用于求单调的时候用的,就比如说排序好的数组,那是递增的或者递减的。如果像出现了下图二次函数那样的怎么求他的最值呢?

二分法早就失去了他的意义了。不过还是可以用三分法来实现的,就是二分中再来二分。比如我们定义了L和R,m = (L + R) / 2,mm = (mid + R) / 2; 如果mid靠近极值点,则R = mm;否则就是mm靠近极值点,则L = m;这样的话,极值还是可以求的。具体的还是看看题目吧。
zoj 3203 Light Bulb
--------------------------------------------------------------------------------
Time Limit: 1 Second Memory Limit: 32768 KB
--------------------------------------------------------------------------------
Compared to wildleopard's wealthiness, his brother mildleopard is rather poor. His house is narrow and he has only one light bulb in his house. Every night, he is wandering in his incommodious house, thinking of how to earn more money. One day, he found that the length of his shadow was changing from time to time while walking between the light bulb and the wall of his house. A sudden thought ran through his mind and he wanted to know the maximum length of his shadow.

Input
The first line of the input contains an integer T (T <= 100), indicating the number of cases.
Each test case contains three real numbers H, h and D in one line. H is the height of the light bulb while h is the height of mildleopard. D is distance between the light bulb and the wall. All numbers are in range from 10-2 to 103, both inclusive, and H - h >= 10-2.
Output
For each test case, output the maximum length of mildleopard's shadow in one line, accurate up to three decimal places..
Sample Input
3
2 1 0.5
2 0.5 3
4 3 4
Sample Output
1.000
0.750
4.000
题意很简单,就是人左右走动,求影子L的最长长度。
由图可知,当人走进时,当影子刚好没有投到墙上的时候,是最长的。接着影子到了墙上就变小了,所以可以用三分法来求最值。当然用高数的求导还是可以解决的,只是定义域要注意下。
#include <stdio.h>
int main()
{
int t;
scanf("%d", &t);
while(t--)
{
double h, H, D;
scanf("%lf%lf%lf", &H, &h, &D);
double left = 0, right = D * h / H;
int size = 100;
double mid, midmid, ans1, ans2;
while(size--)
{
mid = (left + right) / 2;
midmid = (mid + right) / 2;
ans1 = ((h*D-H*mid)/(H-h)*H)/((h*D-H*mid)/(H-h)+D)+mid;
ans2 = ((h*D-H*midmid)/(H-h)*H)/((h*D-H*midmid)/(H-h)+D)+midmid;
if(ans1 > ans2) right = midmid;
else left = mid;
}
printf("%.3lf\n", ans1);
}
return 0;
}
这个基本上是模版吧,只是那个函数要自己去写,只要解决了这个函数,就一直让他循环求极值吧,差不多100次就可以找到这个点了。
再来看一道题目
hdu 2438Turn the corner
Time Limit: 3000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 404 Accepted Submission(s): 103
Problem Description
Mr. West bought a new car! So he is travelling around the city.One day he comes to a vertical corner. The street he is currently in has a width x, the street he wants to turn to has a width y. The car has a length l and a width d. Can Mr. West go across the corner?

Input
Every line has four real numbers, x, y, l and w. Proceed to the end of file.
Output
If he can go across the corner, print "yes". Print "no" otherwise.
Sample Input
10 6 13.5 4
10 6 14.5 4
Sample Output
yes
no

其实就是汽车能不能拐弯的问题,告诉你X, Y, l, d判断是否能够拐弯,由下图可知,如果d大于X,Y的话,那么怎么样汽车也过不了。接着就是三分求下图那个最值了,如果到了这个地步,所求的h还是比Y小的话,那么肯定是可以拐弯的。
#include <cstdio> #include <cmath> const double pi = 3.1415926535; int main() { double x, y, l, w; while(scanf("%lf%lf%lf%lf", &x, &y, &l, &w) != EOF) { int size = 100; double left = 0, right = pi / 2; double mid = 0, midmid = 0, ans1, ans2; if(x < w || y < w){printf("no\n"); continue;} while(size--) { mid = (left+right) / 2; midmid = (mid+right) / 2; ans1 = (x-l*sin(mid)-w/cos(mid)) / tan(mid); ans2 = (x-l*sin(midmid)-w/cos(midmid)) / tan(midmid); if(ans1 < ans2) right = midmid; else left = mid; } if(fabs(ans1) > y) printf("no\n"); else printf("yes\n"); } return 0; }
这两题几乎就是用了三分的模版,然后就是简单的公式推导,然后就可以很方便的实现了,接着我们来看看稍微复杂点的吧。
xmu 1125.越野车大赛
Description
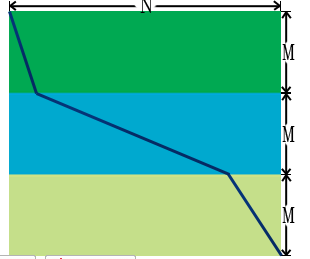
TheBeet正在参加一场越野车大赛。比赛的场地如右图:共分三块,每一块地面的长宽均为N与M,但地表情况不同,越野车在这段路面上的最高速度也不同。蓝色线表示TheBeet可能的行车路线。
比赛的要求是要求选手从比赛的场地左上角驾车至右下角。TheBeet想知道如果他在所有路段都以最快速度行驶(不考虑加速阶段),最快能在多少时间内完成比赛。
Input
输入数据的第一行为两个正整数N M(N<=3000,M<=1000),表示一块路面的长和宽。
第二行为三个正整数S1,S2,S3(0<S1,S2,S3<=100),从上至下依次表示各个路面上越野车的最高速度。
Output
输出一个实数表示TheBeet最快能在多少时间内完成比赛。请输出一个尽可能精确的数字,控制误差在±0.000001的内。
Sample Input
30 10
2 5 3
Sample Output
13.7427361525
Hint
如果你的输出和结果的相差在0.000001之内,则认为是正确答案。
分析下该题,其实也是要求求最值,不过这个最值是满足两个地方的要求,想想和三分有什么关系呢?其实还是一样的,只是这里要用到两个三分了,不仅仅满足第一个要求,第二个要求也要一并给他满足了,接着这样的最值就是题目所要求的了。下面是搓搓的代码:
#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
const double pi = 3.141592654;
inline double dis(double x1, double y1, double x2, double y2)
{
return sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2));
}
int main()
{
double n, m, a, b, c;
while(cin >> n >> m)
{
cin >> a >> b >> c;
double left1 = 0, right1 = pi / 2;
double mid1, midmid1, mid2, midmid2, ans1, ans11, ans2, ans3, ans4, ans5, ans44, ans55;
int size = 30;
while(size--)
{
mid1 = (left1 + right1) / 2;
midmid1 = (mid1 + right1) / 2;
ans1 = dis((n - m / tan(mid1)), m, n, 0);
ans11 = dis((n - m / tan(midmid1)), m, n, 0);
int size1 = 30;
double left2 = 0, right2 = pi / 2;
while(size1--)
{
mid2 = (left2 + right2) / 2;
midmid2 = (mid2 + right2) / 2;
ans2 = dis((n - m / tan(mid1)), m, (n - m / tan(mid1) - m / tan(mid2)), 2*m);
ans3 = dis((n - m / tan(mid1)), m, (n - m / tan(mid1)- m / tan(midmid2)), 2*m);
ans4 = ans1 / c + ans2 / b + dis(0, 3*m, (n - m / tan(mid1) - m / tan(mid2)), 2*m) / a;
ans5 = ans1 / c + ans3 / b + dis(0, 3*m, (n - m / tan(mid1) - m / tan(midmid2)), 2*m) / a;
if(ans4 > ans5) left2 = mid2;
else right2 = midmid2;
}
left2 = 0, right2 = pi / 2;
size1 = 30;
while(size1--)
{
mid2 = (left2 + right2) / 2;
midmid2 = (mid2 + right2) / 2;
ans2 = dis((n - m / tan(midmid1)), m, (n - m / tan(midmid1) - m / tan(mid2)), 2*m);
ans3 = dis((n - m / tan(midmid1)), m, (n - m / tan(midmid1) - m / tan(midmid2)), 2*m);
ans44 = ans11 / c + ans2 / b + dis(0, 3 * m, (n - m / tan(midmid1) - m / tan(mid2)), 2*m) / a;
ans55 = ans11 / c + ans3 / b + dis(0, 3 * m, (n - m / tan(midmid1) - m / tan(midmid2)),2*m) /a;
if(ans44 > ans55) left2 = mid2;
else right2 = midmid2;
}
if(ans4 > ans44) left1 = mid1;
else right1 = midmid1;
}
printf("%.10lf\n", ans4);
}
return 0;
}
至此,三分法就是这样的了,很简单吧,总结下,就是要求出那个公式,然后调用那个框架。只要理解了原理,题目都是换汤不换药的。小憩片刻,还是回公司看看书去吧。这时代,不看书,不多学点东西,会被时代淘汰的。。。。。。