Ipad,IPhone（矩阵求递推项+欧拉定理）

Ipad,IPhone

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)

Total Submission(s): 100 Accepted Submission(s): 46

Problem Description

In ACM_DIY, there is one master called “Lost”. As we know he is a “-2Dai”, which means he has a lot of money.
  
Well, Lost use Ipad and IPhone to reward the ones who solve the following problem.
  
In this problem, we define F( n ) as :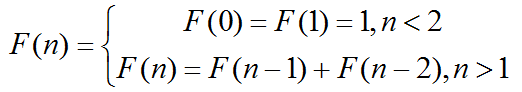
  
Then Lost denote a function G(a,b,n,p) as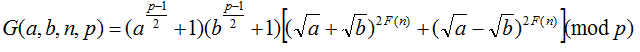

Here a, b, n, p are all positive integer!
If you could tell Lost the value of G(a,b,n,p) , then you will get one Ipad and one IPhone!

 

Input

The first line is one integer T indicates the number of the test cases. (T <= 100)
Then for every case, only one line containing 4 positive integers a, b, n and p.
(1 ≤a, b, n, p≤2*10⁹ , p is an odd prime number and a,b < p.)

 

Output

Output one line,the value of the G(a,b,n,p) .

 

Sample Input

4
2 3 1 10007
2 3 2 10007
2 3 3 10007
2 3 4 10007

 

Sample Output

40
392
3880
9941

 

Author

AekdyCoin

 

Recommend

notonlysuccess

/*
题意：给出如图所示的式子，让你求出值

初步思路：斐波那契数列后推一位，直接求是不可以的，因为几十项就会爆，所以用到矩阵求斐波那契数列，式子的前半部分可以直接用快速幂求得
    现在有一个问题，就是X^t mod q是不是等于 X^(t mod q) 先爆一发试试

#错误：上面的想法显然是错误的！

#改进：后边的比较麻烦,后半部分用矩阵求递推项，这几天看这个好麻烦啊，转专业没学线性代数，构造矩阵就麻烦死了。
    首先令    Xn=(sqrt(a)+sqrt(b))^(2*fn)
            Yn=(sqrt(a)-sqrt(b))^(2*fn)
    然后得    X1=a+b+2*sqrt(ab)
            Y1=a+b-2*sqrt(ab)
        得    X1+Y1=2*(a+b)
            X1*Y1=(a-b)^2
由韦达定理
求特征方程：u^2-2*(a+b)*u+(a-b)^2=0;

得特征方程    Zn^2=2*(a+b)*Zn-1 - (a-b)^2*Zn-2

由此构造矩阵 Zn=(Z0,Z1)*{ 0 , -(a-b)^2 }^n
                        { 1 , 2*(a+b)  }    
                        
*/
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll mod;
/******************快速幂*************************/
ll my_pow(ll a,ll b){
    ll ans = 1;
    while(b){
        if (b%2)
            ans = (ans*a)%mod;
        b/=2;
        a=(a*a)%mod;
    }
    return ans;
}
/******************快速幂*************************/

/*******************矩阵快速幂**********************/
struct Mar{
    ll mat[2][2];
};
Mar E={1,0,0,1},unit2={0,1,1,1};
Mar mul(Mar a,Mar b){
    ll fumod(ll);
    Mar ans={0,0,0,0};
    for (int i = 0; i < 2; ++i)
        for (int j = 0; j < 2; ++j)
            for (int k = 0; k <2; ++k){
                ans.mat[i][j]+=(a.mat[i][k]*b.mat[k][j])%mod;
                ans.mat[i][j]%=mod;
        }
    return ans;
}
Mar pow2(Mar a,ll n){
    Mar ans = E;
    while(n){
        if (n%2)
            ans = mul(ans,a);
        n/=2;
        a=mul(a,a);
    }
    return ans;
}
/*******************矩阵快速幂**********************/

ll fib(ll n){//求斐波那契数列
    Mar uu={1,1,1,1};
    Mar p=pow2(unit2,n);
    p=mul(uu,p);
    return p.mat[0][0];
}
int main(){
    //freopen("in.txt","r",stdin);
    ll T,a,b,n,p;
    scanf("%lld",&T);
    while(T--){
        scanf("%lld%lld%lld%lld",&a,&b,&n,&p);
        mod = p;
        //前边的两项
        ll temp1=(my_pow(a,(p-1)/2)+1)%mod;
        ll temp2=(my_pow(b,(p-1)/2)+1)%mod;
        
        if (!temp1 || !temp2){cout << "0" << endl;continue;}
        --mod;
        
        ll fn=fib(n);
        ++mod;
        
        //矩阵求后边的两项
        Mar unit={2,2*(a+b)%mod,1,1};
        Mar tmp1={0,-(a-b)*(a-b)%mod,1,2*(a+b)%mod};
        Mar p=pow2(tmp1,fn);
        p=mul(unit,p);
        ll pn=p.mat[0][0];
        ll ans = pn%mod*temp1%mod*temp2%mod;
        while(ans < 0)ans+=mod;
        printf("%lld
",ans);
    }
    return 0;
}