Description
Alice gets two sequences A and B. A easy problem comes. How many pair of sequence A' and sequence B' are same. For example, {1,2} and {1,2} are same. {1,2,4} and {1,4,2} are not same. A' is a subsequence of A. B' is a subsequence of B. The subsequnce can be not continuous. For example, {1,1,2} has 7 subsequences {1},{1},{2},{1,1},{1,2},{1,2},{1,1,2}. The answer can be very large. Output the answer mod 1000000007.
Input
The input contains multiple test cases.
For each test case, the first line cantains two integers

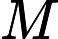





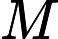





 . The next line contains N integers. The next line followed M integers. All integers are between 1 and 1000.
. The next line contains N integers. The next line followed M integers. All integers are between 1 and 1000.
For each test case, the first line cantains two integers


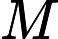





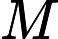





 . The next line contains N integers. The next line followed M integers. All integers are between 1 and 1000.
. The next line contains N integers. The next line followed M integers. All integers are between 1 and 1000.Output
For each test case, output the answer mod 1000000007.
Sample Input
3 2 1 2 3 2 1 3 2 1 2 3 1 2
Sample Output
2 3
/*
给你两个序列,让你求有多少个公共子序列。
dp[i][j]表示第一串到i位置,第二串到j位置,最多有多少相同子序列;
那么状态转移方程就变成了dp[i][j]=dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1];
这里列一个矩阵更好帮助理解
*/
# include <iostream>
# include <cstring>
# include <stdio.h>
using namespace std;
const int MAX = 1005;
const long long int mod = 1000000007;
int a[MAX], b[MAX];
long long int dp[MAX][MAX];
int main()
{
int n, m;
while(scanf("%d%d",&n,&m))
{
for(int i = 1; i <= n; i++)
scanf("%d",&a[i]);
for(int i = 1; i <= m; i++)
scanf("%d",&b[i]);
memset(dp, 0, sizeof(dp));
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
{
if(a[i] == b[j])
dp[i][j] = (dp[i - 1][j] + dp[i][j - 1] + 1) % mod;
else
dp[i][j] = (dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + mod)%mod;//注意这里很可能出现负数
}
printf("%d
",dp[n][m]);
}
return 0;
}