吉布斯效应 Gibbs effect

将具有不连续点的周期函数（如矩形脉冲)进行傅立叶级数展开后，选取有限项进行合成。当选取的项数越多，在所合成的波形中出现的峰起越靠近原信号的不连续点。当选取的项数很大时，该峰起值趋于一个常数，大约等于总跳变值的9%。这种现象称为吉布斯效应。

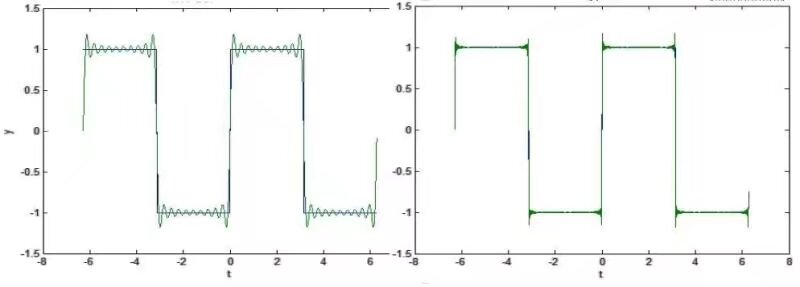
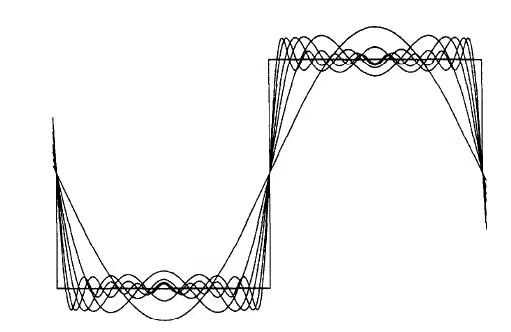
 吉布斯效应:当选用的傅里叶级数的项数增多时，更接近于原周期函

 吉布斯效应

如上图示例，当选用的傅里叶级数的项数增多时，更接近于原周期函数。

我的理解就是:离散信号也可以用傅里叶级数表示，而且选取的有效项越多，越接近原始信号。