题目链接:POJ 2451
Problem Description
Prince Remmarguts solved the CHESS puzzle successfully. As an award, Uyuw planned to hold a concert in a huge piazza named after its great designer Ihsnayish.
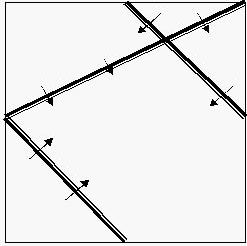
The piazza in UDF - United Delta of Freedom’s downtown was a square of [0, 10000] * [0, 10000]. Some basket chairs had been standing there for years, but in a terrible mess. Look at the following graph.
In this case we have three chairs, and the audiences face the direction as what arrows have pointed out. The chairs were old-aged and too heavy to be moved. Princess Remmarguts told the piazza's current owner Mr. UW, to build a large stage inside it. The stage must be as large as possible, but he should also make sure the audience in every position of every chair would be able to see the stage without turning aside (that means the stage is in the forward direction of their own).
To make it simple, the stage could be set highly enough to make sure even thousands of chairs were in front of you, as long as you were facing the stage, you would be able to see the singer / pianist – Uyuw.
Being a mad idolater, can you tell them the maximal size of the stage?
Input
In the first line, there's a single non-negative integer N (N <= 20000), denoting the number of basket chairs. Each of the following lines contains four floating numbers x1, y1, x2, y2, which means there’s a basket chair on the line segment of (x1, y1) – (x2, y2), and facing to its LEFT (That a point (x, y) is at the LEFT side of this segment means that (x – x1) * (y – y2) – (x – x2) * (y – y1) >= 0).
Output
Output a single floating number, rounded to 1 digit after the decimal point. This is the maximal area of the stage.
Sample Input
3
10000 10000 0 5000
10000 5000 5000 10000
0 5000 5000 0
Sample Output
54166666.7
Source
POJ Monthly, Zeyuan Zhu
Hint
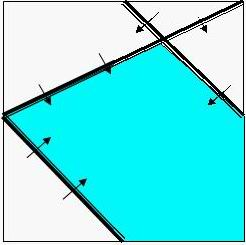
Sample input is the same as the graph above, while the correct solution for it is as below:
I suggest that you use Extended in pascal and long double in C / C++ to avoid precision error. But the standard program only uses double.
Solution
题意
给定一个正方形的边界和 (n) 个向量,求围出的多边形的核的面积。
题解
半平面交
半平面交求多边形的核的模板题。
POJ 的 g++ 好像经常用 long double 才能过。
Code
#include <cstdio>
#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long ll;
typedef long double db;
const db eps = 1e-10;
const db pi = acos(-1.0);
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll maxn = 1e5 + 10;
inline int dcmp(db x) {
if(fabs(x) < eps) return 0;
return x > 0? 1: -1;
}
class Point {
public:
double x, y;
Point(double x = 0, double y = 0) : x(x), y(y) {}
inline void input() {
scanf("%lf%lf", &x, &y);
}
bool operator<(const Point &a) const {
return (!dcmp(x - a.x))? dcmp(y - a.y) < 0: x < a.x;
}
bool operator==(const Point &a) const {
return dcmp(x - a.x) == 0 && dcmp(y - a.y) == 0;
}
db dis2(const Point a) {
return pow(x - a.x, 2) + pow(y - a.y, 2);
}
db dis(const Point a) {
return sqrt(dis2(a));
}
db dis2() {
return x * x + y * y;
}
db dis() {
return sqrt(dis2());
}
Point operator+(const Point a) {
return Point(x + a.x, y + a.y);
}
Point operator-(const Point a) {
return Point(x - a.x, y - a.y);
}
Point operator*(double p) {
return Point(x * p, y * p);
}
Point operator/(double p) {
return Point(x / p, y / p);
}
db dot(const Point a) {
return x * a.x + y * a.y;
}
db cross(const Point a) {
return x * a.y - y * a.x;
}
db ang(Point a) {
return acos((a.dis() * dis()) / dot(a));
}
};
typedef Point Vector;
Point p[maxn], ip[maxn];
class Line {
public:
Point s, e;
db angle;
Line() {}
Line(Point s, Point e) : s(s), e(e) {}
inline void input() {
s.input();e.input();
}
bool operator<(const Line &a) const {
Line l = a;
if(dcmp(angle - l.angle) == 0) {
return l.toLeftTest(s) == 1;
}
return angle < l.angle;
}
void get_angle() {
angle = atan2(e.y - s.y, e.x - s.x);
}
int toLeftTest(Point p) {
if((e - s).cross(p - s) > 0) return 1;
else if((e - s).cross(p - s) < 0) return -1;
return 0;
}
int linecrossline(Line l) {
if(dcmp((e - s).cross(l.e - l.s)) == 0) {
if(dcmp((l.s - e).cross(l.e - s)) == 0) {
return 0;
}
return 1;
}
return 2;
}
Point crosspoint(Line l) {
db a1 = (l.e - l.s).cross(s - l.s);
db a2 = (l.e - l.s).cross(e - l.s);
db x = (s.x * a2 - e.x * a1) / (a2 - a1);
db y = (s.y * a2 - e.y * a1) / (a2 - a1);
if(dcmp(x) == 0) x = 0;
if(dcmp(y) == 0) y = 0;
return Point(x, y);
}
};
Line l[maxn], q[maxn];
db half_plane(int cnt) {
sort(l + 1, l + 1 + cnt);
int tmp = 1;
for(int i = 2; i <= cnt; ++i) {
if(dcmp(l[i].angle - l[tmp].angle) == 1) l[++tmp] = l[i];
}
cnt = tmp;
int head = 1, tail = 2;
q[1] = l[1], q[2] = l[2];
for(int i = 3; i <= cnt; ++i) {
while(head < tail && l[i].toLeftTest(q[tail].crosspoint(q[tail - 1])) == -1) {
--tail;
}
while(head < tail && l[i].toLeftTest(q[head].crosspoint(q[head + 1])) == -1) {
++head;
}
q[++tail] = l[i];
}
while(head < tail && q[head].toLeftTest(q[tail].crosspoint(q[tail - 1])) == -1) {
--tail;
}
while(head < tail && q[tail].toLeftTest(q[head].crosspoint(q[head + 1])) == -1) {
++head;
}
if(tail - head + 1 <= 2) {
return 0.0;
}
tmp = 0;
for(int i = head; i < tail; ++i) {
ip[++tmp] = q[i].crosspoint(q[i + 1]);
}
ip[++tmp] = q[head].crosspoint(q[tail]);
db ans = 0;
for(int i = 3; i <= tmp; ++i) {
ans += (ip[i - 1] - ip[1]).cross(ip[i] - ip[1]);
}
ans *= 0.5;
if(dcmp(ans) == 0) ans = 0.0;
return ans;
}
int main() {
int n;
int _ = 0;
while(~scanf("%d", &n)) {
l[1] = Line(Point(0, 0), Point(10000, 0)); l[1].get_angle();
l[2] = Line(Point(10000, 0), Point(10000, 10000)); l[2].get_angle();
l[3] = Line(Point(10000, 10000), Point(0, 10000)); l[3].get_angle();
l[4] = Line(Point(0, 10000), Point(0, 0)); l[4].get_angle();
for(int i = 1; i <= n; ++i) {
l[4 + i].input();
l[4 + i].get_angle();
}
// cout << ++_ << " ";
printf("%.1lf
", half_plane(n + 4));
}
return 0;
}