洛谷 P3187 BZOJ 1185 [HNOI2007]最小矩形覆盖 (旋转卡壳)

题目链接：

洛谷 P3187 [HNOI2007]最小矩形覆盖

BZOJ 1185: [HNOI2007]最小矩形覆盖

Description

给定一些点的坐标，要求求能够覆盖所有点的最小面积的矩形，

输出所求矩形的面积和四个顶点坐标

Input

第一行为一个整数n（3<=n<=50000）

从第2至第n+1行每行有两个浮点数，表示一个顶点的x和y坐标，不用科学计数法

Output

第一行为一个浮点数，表示所求矩形的面积（精确到小数点后5位），

接下来4行每行表示一个顶点坐标，要求第一行为y坐标最小的顶点，

其后按逆时针输出顶点坐标.如果用相同y坐标，先输出最小x坐标的顶点

Sample Input

6 1.0 3.00000

1 4.00000

2.0000 1

3 0.0000

3.00000 6

6.0 3.0

Sample Output

18.00000

3.00000 0.00000

6.00000 3.00000

3.00000 6.00000

0.00000 3.00000

Solution

旋转卡壳

旋转卡壳求最小面积多边形外接矩形的模板题。

精度问题卡了好久，-0.00000 被卡了，真的毒瘤。

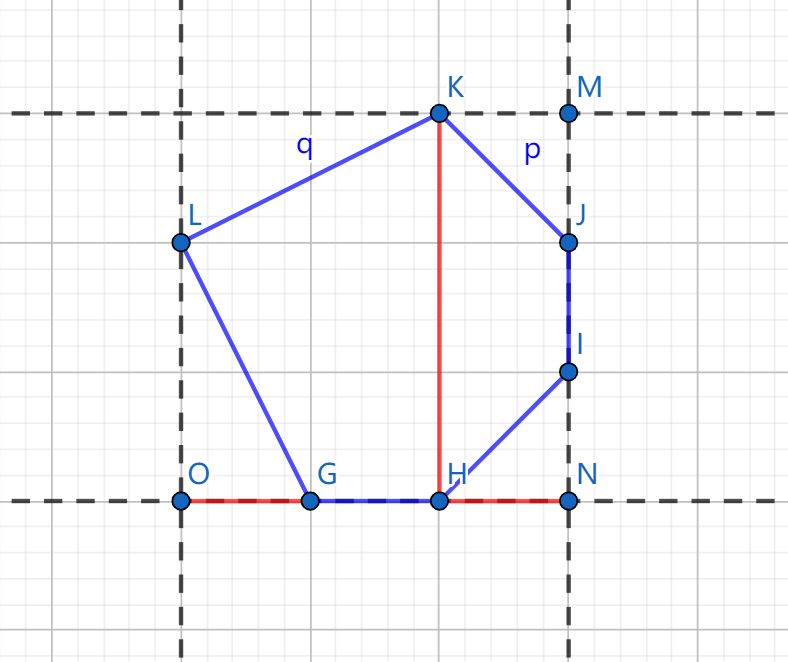
首先求凸包，然后用旋转卡壳维护最左边的点，最上面的点和最右边的点即可。(下图中的 (L), (K), (J) 点)

最上面的点的求法类似凸包的直径，就是求对踵点，用叉积维护即可。

最左边和最右边的点就是投影最大的点。用点积维护。

注：比较的时候最好不要直接用比较运算符。

Code

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const double eps = 1e-8;
const int maxn = 100000 + 5;

int n;

inline int dcmp(double x) {
    if(fabs(x) < eps) return 0;
    return x > 0? 1: -1;
}

class Point {
public:
    double x, y;
    Point(double x = 0, double y = 0) : x(x), y(y) {}
    Point operator+(Point a) {
        return Point(a.x + x, a.y + y);
    }
    Point operator-(Point a) {
        return Point(x - a.x, y - a.y);
    }
    bool operator<(const Point &a) const {
        if (x == a.x)
            return y < a.y;
        return x < a.x;
    }
    Point operator*(double a) {
        return Point(x * a, y * a);
    }
    bool operator==(const Point &a) const {
        if (x == a.x && y == a.y)
            return 1;
        return 0;
    }
    double len() {
        return sqrt(x * x + y * y);
    }
    double dis2(const Point a) {
        return pow(x - a.x, 2) + pow(y - a.y, 2);
    }
    double dis(const Point a) {
        return sqrt(dis2(a));
    }
};

Point ans[10];

typedef Point Vector;

double cross(Vector a, Vector b) {
    return a.x * b.y - a.y * b.x;
}

double dot(Vector a, Vector b) {
    return a.x * b.x + a.y * b.y;
}

typedef vector<Point> Polygon;
Polygon Andrew(Polygon P) {
    int n = P.size(), k = 0;
    vector<Point> H(2 * n);
    sort(P.begin(), P.end());
    for (int i = 0; i < n; ++i) {
        while (k >= 2 && cross(H[k - 1] - H[k - 2], P[i] - H[k - 2]) < eps) {
            k--;
        }
        H[k++] = P[i];
    }
    int t = k + 1;
    for (int i = n - 1; i > 0; --i) {
        while (k >= t && cross(H[k - 1] - H[k - 2], P[i - 1] - H[k - 2]) < eps) {
            k--;
        }
        H[k++] = P[i - 1];
    }
    H.resize(k - 1);
    return H;
}

double rotating_caliper(Polygon v) {
    double min_s = 1e18;
	int cnt = v.size();
    v.push_back(v[0]);
    int u = 1, r = 1, l = 1;
    for (int i = 0; i < cnt; ++i) {
        // 最上面的点
        while (dcmp(fabs(cross(v[u] - v[i], v[i + 1] - v[i])) - fabs(cross(v[u + 1] - v[i], v[i + 1] - v[i]))) <= 0) {
            u = (u + 1) % cnt;
        }

        // 最右边的点
        while (dcmp(dot(v[r] - v[i], v[i + 1] - v[i]) - dot(v[r + 1] - v[i], v[i + 1] - v[i])) <= 0) {
            r = (r + 1) % cnt;
        }

        if(!i) l = r;

        // 最左边的点
        while (dcmp(dot(v[l] - v[i], v[i + 1] - v[i]) - dot(v[l + 1] - v[i], v[i + 1] - v[i])) >= 0) {
            l = (l + 1) % cnt;
        }
        double d = v[i].dis(v[i + 1]);
        double R = dot(v[r] - v[i], v[i + 1] - v[i]) / d; 
        double L = dot(v[l] - v[i], v[i + 1] - v[i]) / d;
        double ll = R - L;
        double dd = fabs(cross(v[u] - v[i], v[i + 1] - v[i])) / d;
        double s = ll * dd;
        if(s < min_s) {
            min_s = s;
            ans[0] = v[i] + (v[i + 1] - v[i]) * (R / d);
            ans[1] = ans[0] + (v[r] - ans[0]) * (dd / v[r].dis(ans[0]));
            ans[2] = ans[1] + (v[i] - ans[0]) * (ll / R);
            ans[3] = ans[2] + (ans[0] - ans[1]);
        }
    }
    return min_s;
}

int main() {
    scanf("%d", &n);
    Polygon s;
    for(int i = 0; i < n; ++i) {
        Point p;
        scanf("%lf%lf", &p.x, &p.y);
        s.push_back(p);
    }
    Polygon p = Andrew(s);
    double d = rotating_caliper(p);
    printf("%.5lf
", d);
    double miny = 1e18;
    int index = 1;
    for(int i = 0; i < 4; ++i) {
        if(dcmp(ans[i].x) == 0) ans[i].x = 0;
        if(dcmp(ans[i].y) == 0) ans[i].y = 0;
        if(ans[i].y < miny) {
            miny = ans[i].y;
            index = i;
        }
    }
    double minx = 1e18;
    for(int i = 0; i < 4; ++i) {
        if(ans[i].y == miny && ans[i].x < minx) {
            minx = ans[i].x;
            index = i;
        }
    }
    for(int i = 0; i < 4; ++i)  {
        printf("%.5lf %.5lf
", ans[(i + index) % 4].x, ans[(i + index) % 4].y);
    }
    return 0;
}