2016012024+小学四则运算练习软件项目报告
代码仓库地址为:https://git.coding.net/wujy123/arithmetic.git
测试效果见生成的result.txt
一、前言
这两周的学习让我收获满满。我原来一直学的是前端js的相关知识,对于java不怎么熟悉,笨鸟就要先飞,上周我用了近一周的时间复习了java的相关知识后才开始写这次的作业。虽然完成的功能不是很完善,但我学习到了很多,也让我重新学习java有了很好的开端
二、需求分析
小学生计算能力需要通过练习大量的运算题目得到锻炼,因此很多老师让家长每天给学生出相应的练习题。为了方便老师的教学任务,同时减轻家长的负担,现在需要一个可以出四则混合运算的小型软件。
需求:
1.通过程序接收一个数字n,产生n道加减乘除练习题。
2.判断传入参数是否合法,是否是在0-1000之间的整数。
3.考虑到我们的用户对象是小学生,每个数字在0-100之间,运算符3-5个
4.由于小学生的知识储备,故运算过程不能出现负数(减法时注意)和非整数(除法时注意)
5.计算出练习题结果
6.所有信息输出到result.txt文件
三、功能设计
基础功能:
程序可接收一个输入参数n,然后随机产生n道加减乘除练习题,每个数字在 0 和 100 之间,运算符在3个到5个之间。
为了让小学生得到充分锻炼,每个练习题至少要包含2种运算符。同时,由于小学生没有分数与负数的概念,你所出的练习题在运算过程中不得出现负数与非整数,比如不能出 3/5+2=2.6,2-5+10=7等算式。
练习题生成好后,将你的学号与生成的n道练习题及其对应的正确答案输出到文件“result.txt”中,不要输出额外信息,文件目录与程序目录一致。
当程序接收的参数为4时,以下为输出文件示例。

扩展功能:
支持有括号的运算式,包括出题与求解正确答案。注意,算式中存在的括号必须大于2个,且不得超过运算符的个数。
扩展程序功能支持真分数的出题与运算,例如:1/6 + 1/8 + 2/3= 23/24。注意在实现本功能时,需支持运算时分数的自动化简,比如 1/2+1/6=2/3,而非4/6。
四、设计实现:
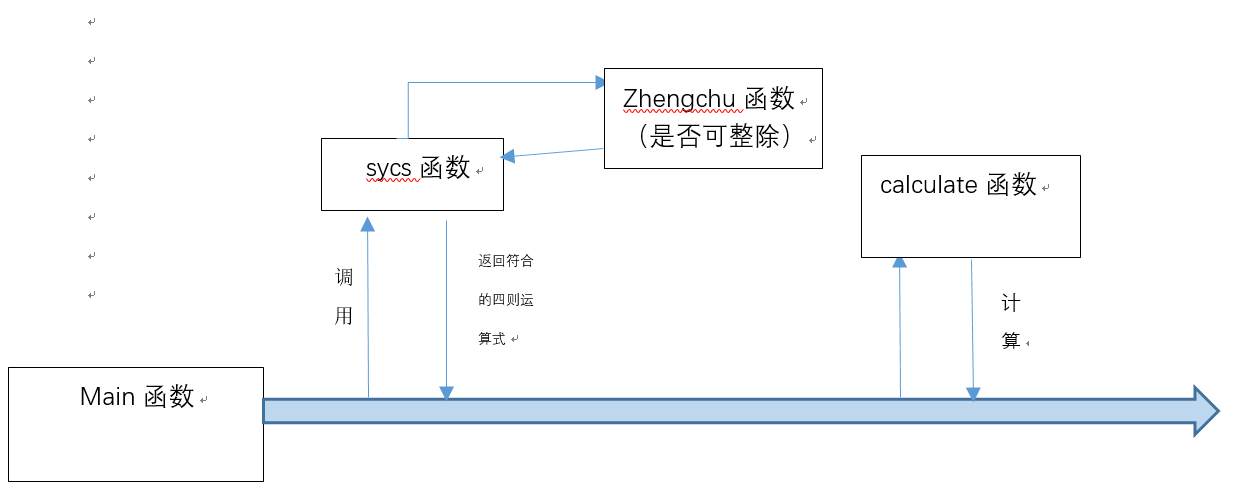
在实现过程中,我只用了一个Main类,功能全由对Main类的方法的调用来实现实现。
用到的函数有:
main函数:
主函数,负责接收参数n,判断参数n的合法性,调用函数产生合格的四则运算式,计算运算式结果并将式子+结果通过打印输出流输出到文件中的功能。
scys函数:
生成一个符合要求的四则运算式(两种以上的运算符且可以整除,不会产生分数)。
zhengchu函数:
判断是否可以整除
calculate 函数:
用于计算生成的四则运算式的结果,假如结果小于0,就重新生成一个式子
yuefen 函数:
对结果寻找他们的最大公因式来实现约分
五、算法详解:
生成四则运算式:
由于有整数和分数两种计算式,我就先生成一个小于接收到的参数n的随机数zs,从而在下一步时生成zs个整数四则运算式和n-zs个分数式
生成整数式:
先随机生成一个3-5的随机数用于表示这个式子的运算符数量,再通过for循环每循环一次就生成一个1-99的随机数(运算数)和一个0-3的随机数(对应运算符)“拼接”在字符串中,相邻的两个运算符不能相同,并判断假如是除号,判断是否可以整除:
// 判断是否整除 private static int zhengchu(int a, int b) { if (a % b != 0) { for (int i = a - 1; i > 0; i--) { if (a % i == 0) { return i; } } return 1; } else { return b; } }
判断后,再附加一个数在字符串中,就生成一个符合要求的整数四则运算式.。
完整代码如下:
// 生成一个式子 public String scys() { Random random = new Random(); int n = random.nextInt(3) + 3;// 3-5的随机数——运算符数量 String str = new String(); int[] arr = new int[n + 1];// 把数字存进去 int[] ops = new int[2]; // 避免出现同一个字符 int prec = 0; for (int j = 0; j < n; j++) { // 附加 ops[j % 2] = random.nextInt(4);// 随机选择一个运算符 int c;// 本次添加的运算符 if (j == 0) { c = ops[0]; } else { while (ops[j % 2] == ops[(j + 1) % 2]) { ops[j % 2] = random.nextInt(4);// 避免出现重复字符 } c = ops[j % 2]; } // int c=(int)(Math.random()*3);//0-3,对应四个运算符 // String p=String.valueOf(ope[c]); //随机选择某个运算符 int a = (int) (Math.random() * 98) + 1; if ((j != 0) && (prec == 3)) { a = zhengchu(arr[j - 1], a); } arr[j] = a; str += a + String.valueOf(ope[c]); prec = c; // System.out.print(a+p); } int b = (int) (Math.random() * 98) + 1; arr[n] = b; // System.out.println(arr); str += b; // System.out.println(str); return str; }
计算:
熟悉js的人都知道js中的eval()函数可以将字符串算出结果来。引JavaScript中的eval()就可以很轻松的完成计算,参见博客: https://blog.csdn.net/msyqmsyq/article/details/52954833 代码如下:
private int calculate(String strs) { ScriptEngine se = new ScriptEngineManager().getEngineByName("JavaScript"); String x; int x2 = 0; try { x = se.eval(strs).toString(); x2 = (int) Double.parseDouble(x); if (x2 < 0) { Main u = new Main(); String str_ = u.scys(); Main calu_ = new Main(); x2 = calu_.calculate(str_); } } catch (ScriptException e) { // TODO Auto-generated catch block e.printStackTrace(); } return x2; }
问过大佬后发现,用逆波兰表达式也可以计算出来,代码如下:
public int calculate(String strs) {//运算混合四则运算方法,利用栈实现 Stack<String> number = new Stack<String>();//创建一个存储数字或符号的栈 Stack<Character> operate = new Stack<Character>();//创建一个存储操作符的栈 int p = (int) (Math.random() * 2) + 2;// p则是产生简单等式的次数,这里取2或3,以保证运算符为3个或5个 String question = MakeQuestion2(p);//调用方法MakeQuestion2(p);产生一个四则运算题目 int len = question.length(); int k = 0;//k是遍历字符串的一个参数 int same=0; for (int j = -1; j < len - 1; j++) {//把题目字符串进行拆分,拆分出数字和运算符,分别进行存储 if (question.charAt(j + 1) == '+' || question.charAt(j + 1) == '-' || question.charAt(j + 1) == '*' || question.charAt(j + 1) == '÷' || question.charAt(j + 1) == '(' || question.charAt(j + 1) == ')' || j == len - 2) { if (j == -1) {//如果第一个就是运算符,即左括号,存储在操作符栈中 operate.push(question.charAt(0)); } else if (j == len - 2) {//如果到字符串的最后了,直接存储到数字栈中 number.push(question.substring(k)); break; } else { if (k <= j) { number.push(question.substring(k, j + 1));//是数字的话存储到数字这个栈中 } if (operate.empty() || question.charAt(j + 1) == '(') {//操作符栈为空或者接下来的符号是左括号的话都直接存储到操作符栈中 operate.push(question.charAt(j + 1)); } else if ((operate.peek() == '+' || operate.peek() == '-') && (question.charAt(j + 1) == '*' || question.charAt(j + 1) == '÷')) { operate.push(question.charAt(j + 1));//如果将要放入栈中的运算符优先级比栈顶元素高,直接入栈 } else if (operate.peek() == '(') {//栈顶是左括号的话,下一个操作符也直接入栈 operate.push(question.charAt(j + 1)); } else if (question.charAt(j + 1) == ')') {//下一个操作符是右括号的话,弹出操作符栈顶元素并压入数字栈中 number.push(String.valueOf(operate.pop())); if (!operate.empty()) { operate.pop(); } } else {//操作符是同等优先级的时候,把栈顶元素弹出压入数字栈中,并把下一个操作符压入操作符栈中 if(operate.peek()==question.charAt(j + 1)){ same++; } number.push(String.valueOf(operate.pop())); operate.push(question.charAt(j + 1)); } } k = j + 2; } } if(same==p+2){//判断题目的符号是否都相同 ifsame=1; } while (!operate.empty()) {//最后把操作符栈中剩余的元素都压入数字栈中 number.push(String.valueOf(operate.pop())); } String[] result = new String[20]; int k1 = 0; while (!number.empty()) {//把数字栈中的元素也就是形成的后缀表达式存储在数组中 result[k1] = number.pop(); k1++; } for (k1 = k1 - 1; k1 >= 0; k1--) {//逆序遍历数组,运算得到的后缀表达式 if (!result[k1].equals("+") && !result[k1].equals("-") && !result[k1].equals("*") && !result[k1].equals("÷")) {//是数字的话,先压入栈中 number.push(result[k1]); } else { int a1 = 0; int b1 = 0; if (!number.empty()) {//弹出两个数进行相应运算 b1 = Integer.parseInt(number.pop()); } if (!number.empty()) { a1 = Integer.parseInt(number.pop()); } if (result[k1].equals("+")) {//如果是加号的话,弹出两个数相加 int c1 = a1 + b1; number.push(String.valueOf(c1)); } else if (result[k1].equals("-")) { int c1 = a1 - b1; number.push(String.valueOf(c1)); } else if (result[k1].equals("*")) { int c1 = a1 * b1; number.push(String.valueOf(c1)); } else { int c1 = a1 / b1; number.push(String.valueOf(c1)); } } } return number.pop());//最后输出问题和答案 }
两种方法都可以计算出结果。
分数表达式:
由于我java的能力有限,只能实现两个分数的加减乘除四则运算并对结果化简,它和未实现的括号一样,都是我下一步要学习并完善的功能
目前代码如下:
// 分数运算 int M, Z; int x1, x2, m1, m2; for (i = 0; i < x - zs; i++) { m1 = 1 + (int) (Math.random() * 99);// 随机生成一个小于99的分母 x1 = 1 + (int) (Math.random() * m1);// 生成一个比分母小的分子,实现真分数 m2 = 1 + (int) (Math.random() * 99);// 随机生成一个小于99的分母 x2 = 1 + (int) (Math.random() * m2);// 生成一个比分母小的分子,实现真分数 int c = (int) (Math.random() * 3);// 生成运算符 if (c == 0) { Z = x1 * m2 + x2 * m1; M = m1 * m2; } else if (c == 1) { Z = x1 * m2 - x2 * m1; M = m1 * m2; } else if (c == 2) { Z = x1 * x2; M = m1 * m2; } else { Z = m1 * x2; M = m2 * x1; } d = yuefen(Z, M); shizi = x1 + "/" + m1 + "+" + x2 + "/" + m2 + "=" + d;
六、测试运行
控制台输出如下:

文件内容如下:

命令行输出如下:
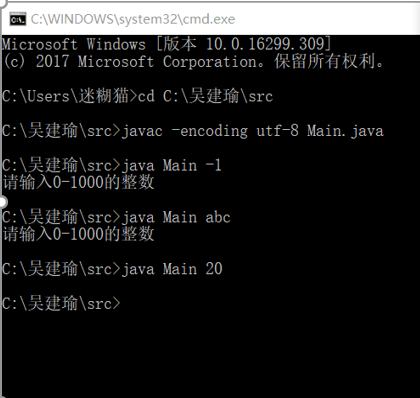
可以看到它只支持0-1000的参数
值得一提的是,刚开始命令行测试时,总是在输入javac -encoding utf-8 Main.java后,报错:非法字符:“ufeff” “需要class,interface或enum”
怎么改都会报这两个错,后来才知道:这是因为我是utf-8-BOM的编码,用Notepad++改成utf-8编码即可。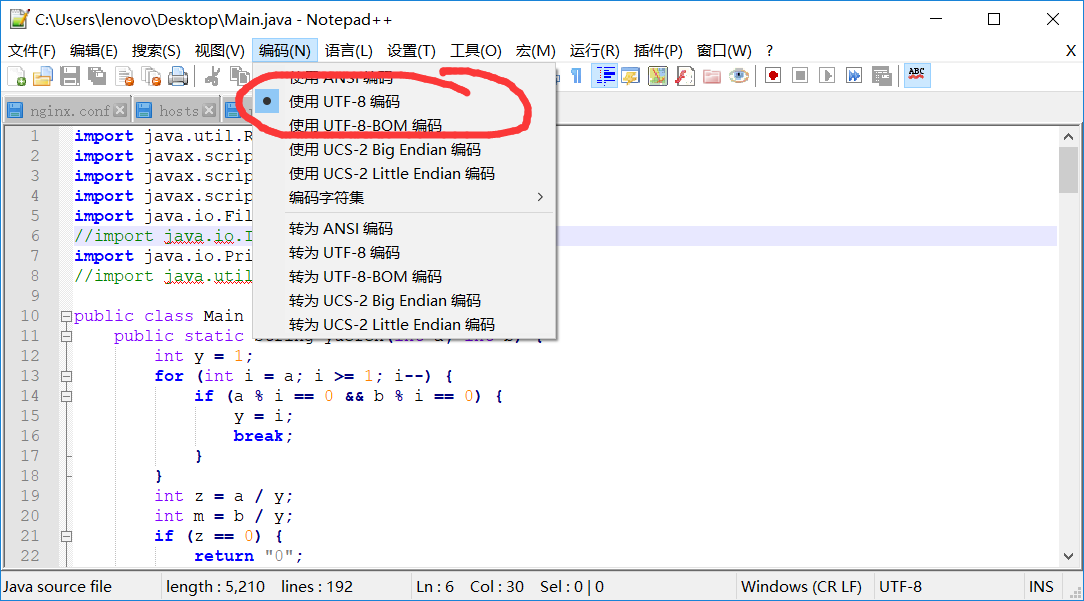
七、代码片段
输出的除号要求是“÷”而不是“/”,但是“÷”无法被eval()函数识别。怎么办呢?
身为一个前台人员,我立即想到了正则表达式,上网一查,java也支持强大的正则表达式,只需要引入
import java.util.regex.Pattern; import java.util.regex.Matcher;
即可。
如:
Main calu = new Main();
shizi = str2.replaceAll("/", "÷") + "=" + calu.calculate(str2);
就可以轻松的实现将“/”换为“÷”的功能!
更多介绍可参考:http://www.runoob.com/java/java-regular-expressions.html https://www.cnblogs.com/xyou/p/7427779.html
八、模块化原则
我写了五个函数来分别实现程序的不同功能:
- 生成一个符合标准的四则运算式(含一种以上运算符)
- 有除号就检查数字是否可以整除,如不能则不断改变,直到获得可以整除的数字。
- 将所有的四则运算式计算出结果,并在计算过程中将不符合条件的式子进行替换。
- 将分数运算式的结果进行约分。
- 负责接收参数n,判断参数n的合法性,调用函数产生合格的四则运算式,计算运算式结果并将式子+结果通过打印输出流输出到文件中。
将代码按照不同的功能分开后,想要修改哪一个部分的代码只需要在相应的函数中修改即可,让我的程序有了一定的独立性,稳定性和移植性。
一开始我将生成四则运算式和整除都放进了main函数里,但这样到了后面发现判断和计算的时候很难调用,于是就又把它放到了函数中来调用。
经过这样的修改,我对软件的模块化设计有了十分清晰和直观地认识,在以后的作业中我会更加注意模块化的设计。
九、psp展示
|
PSP2.1 |
任务内容 |
计划共完成需要的时间(min) |
实际完成需要的时间(min) |
|
Planning |
计划 |
8 |
6 |
|
· Estimate |
· 估计这个任务需要多少时间,并规划大致工作步骤 |
8 |
6 |
|
Development |
开发 |
82 |
88 |
|
· Analysis |
· 需求分析 (包括学习新技术) |
6 |
10 |
|
· Design Spec |
· 生成设计文档 |
5 |
5 |
|
· Design Review |
· 设计复审 (和同事审核设计文档) |
4 |
4 |
|
· Coding Standard |
· 代码规范 (为目前的开发制定合适的规范) |
3 |
3 |
|
· Design |
· 具体设计 |
10 |
12 |
|
· Coding |
· 具体编码 |
36 |
23 |
|
· Code Review |
· 代码复审 |
7 |
9 |
|
· Test |
· 测试(自我测试,修改代码,提交修改) |
13 |
21 |
|
Reporting |
报告 |
9 |
6 |
|
· Test Report |
· 测试报告 |
3 |
2 |
|
· Size Measurement |
· 计算工作量 |
2 |
1 |
|
· Postmortem & Process Improvement Plan |
· 事后总结, 并提出过程改进计划 |
3 |
3 |
十、总结
通过这次作业我比较好地直观感受到了psp流程的必要性。在前期分析需求和功能设计时,我并没有深入地研究,而是简单的审题后就想当然地认为用字符串拼接输出即可,但在后面的代码实现,包括判断整除,运算符的多样性等问题上都出了问题,很难实现。于是不得已又翻上去重新“补”数组。这样的问题也出现在方法的调用上。假如前期就在功能设计上多下功夫,具体代码的时间就 还能再缩短。