汉诺塔问题

       汉诺塔，相信大家已经不再陌生。我觉得也可能是很多人比较迷茫的问题。今天，不知道怎么突然灵光一现，把这个困扰我好久的问题给解决了。分享给大家，希望有所帮助。
      至于问题背景，这里再大致介绍一下,如图：

     

      将一系列木块，从A移动到C，可以借助B，当然，木块的秩序不能改变，即小的木块一定要放在大的木块上面。现在要怎么做呢？

      递归？没错！就是递归，那怎么分析呢？

 

      现在，可以这样想：

 

      ①假设只有一个木块，直接从A移动到C就可以了，问题完成。

 

      ②如果有n个木块，那么把A上面的n-1个木块通过C移动到B上，A上面还剩下最大的一块，直接移动到C上不就好了吗？（至于如何实现n-1块木块的移动，具体细节可以先不考虑，这里只是一种思想）

 

      ③现在的情况变成了B上还有n-1块，A空了，需要把这n-1块移动通过A移动到C上，看一下，这一个步骤是不是和②是相同的呢，只是参数相对发生了一下变化而已。这不就是递归的典型应用吗，最后当只剩下一块的时候就是递归出口。以三块为例,下面是移动的图解过程：

     

 

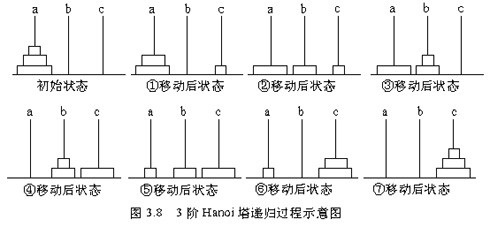
      以上所讲都是在图解的方式下，理解起来应该不是太难。但问题毕竟要用程序来实现，现在我们换一种思路，用算法来分析该问题：

     

/**
n 移动的木块个数
a,b,c 中介木板
*/
hanoi(n,a,b,c)
1    if n==1 then
2        move(a,c)
3    else
4        hanoi(n-1,a,c,b)
5        move(a,c)
6        hanoi(n-1,b,a,c)

 具体分析如下：

      ①代码第一行的四个参数表示为，把a上的n个木块通过b移动到c

      ②如果n为1，那么直接从a移动到c即可，此为递归出口

      ③当n不为1的时候，要先把a上面的n-1个木块通过c移动到b

      ④再把a上面的一个移动到c

      ⑤最后把b上面的n-1个木块通过a移动到c

      OK，问题至此解决！

      当然，使用算法讲解时，只是一种思想，不能跟踪到到每一次的具体实现。如果想跟踪每一步的移动怎么办呢，于是我把代码稍微改动了一下，使之每移动一次都显示出来，完整如下：

#include<stdio.h>
void move(char x,char y)
{
     printf("%c-->%c
",x,y);
}
void Hanoi(int n,char a,char b,char c)
{
    if(n==1)
        move(a,c);
    else
    {
        Hanoi(n-1,a,c,b);
        move(a,c);
        Hanoi(n-1,b,a,c);
    }
}
int main()
{
    int N;
    printf("请输入要移动的木块数：");
    scanf("%d",&N);
    Hanoi(N,'A','B','C');
    return 0;
}

      经过这样的一点小小改动之后，程序就能将每一步如何移动显示出来了，也就达到了跟踪观察的目的。当然，如果有兴趣的话，不妨自己手动追踪一下，肯定会有不一样的感受；

运行结果如下：

     

      最后，经过我的几组测试，貌似发现了一个有趣的结论：采用汉诺塔移动木块时，移动的次数是2的n次方减1（2^n-1，其中n为要移动的木块数），如果有误，恳请大家指点。

 

 

      注：以上代码均在 Code::Blocks + GNU gcc环境下编译运行通过