题目描述
小 Y 是一个爱好旅行的 OIer。她来到 X 国,打算将各个城市都玩一遍。
小Y了解到, X国的 nn 个城市之间有 mm 条双向道路。每条双向道路连接两个城市。 不存在两条连接同一对城市的道路,也不存在一条连接一个城市和它本身的道路。并且, 从任意一个城市出发,通过这些道路都可以到达任意一个其他城市。小 Y 只能通过这些 道路从一个城市前往另一个城市。
小 Y 的旅行方案是这样的:任意选定一个城市作为起点,然后从起点开始,每次可 以选择一条与当前城市相连的道路,走向一个没有去过的城市,或者沿着第一次访问该 城市时经过的道路后退到上一个城市。当小 Y 回到起点时,她可以选择结束这次旅行或 继续旅行。需要注意的是,小 Y 要求在旅行方案中,每个城市都被访问到。
为了让自己的旅行更有意义,小 Y 决定在每到达一个新的城市(包括起点)时,将 它的编号记录下来。她知道这样会形成一个长度为 nn 的序列。她希望这个序列的字典序 最小,你能帮帮她吗? 对于两个长度均为 nn 的序列 AA 和 BB,当且仅当存在一个正整数 xx,满足以下条件时, 我们说序列 AA 的字典序小于 BB。
- 对于任意正整数 1 ≤ i < x1≤i<x,序列 AA 的第 ii 个元素 A_iAi 和序列 BB 的第 ii 个元素 B_iBi 相同。
- 序列 AA 的第 xx 个元素的值小于序列 BB 的第 xx 个元素的值。
输入格式
输入文件共 m + 1m+1 行。第一行包含两个整数 n,m(m ≤ n)n,m(m≤n),中间用一个空格分隔。
接下来 m 行,每行包含两个整数 u,v (1 ≤ u,v ≤ n)u,v(1≤u,v≤n) ,表示编号为 uu 和 vv 的城市之 间有一条道路,两个整数之间用一个空格分隔。
输出格式
输出文件包含一行,nn 个整数,表示字典序最小的序列。相邻两个整数之间用一个 空格分隔。
输入输出样例
6 5 1 3 2 3 2 5 3 4 4 6
1 3 2 5 4 6
6 6 1 3 2 3 2 5 3 4 4 5 4 6
1 3 2 4 5 6
说明/提示
【数据规模与约定】
对于 100\%100% 的数据和所有样例, 1 le n le 50001≤n≤5000 且 m = n − 1 或 m = nm=n 。
对于不同的测试点, 我们约定数据的规模如下:
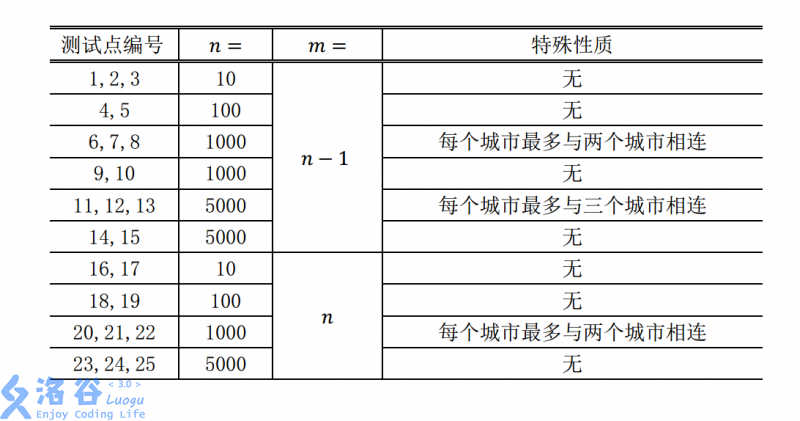
题解;那个啥基环图也不是很会…60分够了恩。
#include<cstdio> #include<iostream> #include<algorithm> #include<cstring> #include<cmath> #include<cstdlib> using namespace std; const int N=5001; int n,m,xx,yy; bool f[N][N]; int k,a[N]; bool vis[N]; void dfs1(int x,int now){ if(now==n) return; bool flag=0; for(int i=1;i<=n;i++){ if(vis[i]==0 && f[x][i]==1){ vis[i]=1; flag=1; a[k++]=i; dfs1(i,now+1); } } if(flag==1) return; } void dfs2(int x,int now){ if(now==n) return; bool flag=0; for(int i=1;i<=n;i++){ if(vis[i]==0 && f[x][i]==1){ vis[i]=1; flag=1; a[k++]=i; dfs2(i,now+1); } } if(flag==1) return; } int main(){ scanf("%d %d",&n,&m); for(int i=1;i<=m;i++){ scanf("%d %d",&xx,&yy); f[xx][yy]=f[yy][xx]=1; } if(m==n-1){ vis[1]=1; a[k++]=1; dfs1(1,0); for(int i=0;i<n;i++) printf("%d ",a[i]); } if(m==n){ vis[1]=1; a[k++]=1; dfs2(1,0); for(int i=0;i<n;i++) printf("%d ",a[i]); } //I am the best return 0; }