【洛谷 3884】二叉树问题

题目描述

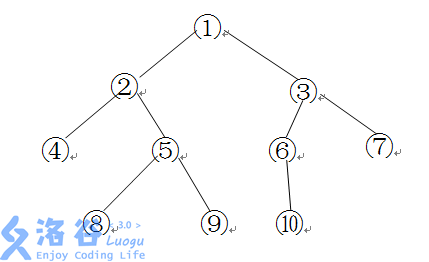
如下图所示的一棵二叉树的深度、宽度及结点间距离分别为：

深度：4 宽度：4（同一层最多结点个数）

结点间距离： ⑧→⑥为8 (3×2+2=8)

⑥→⑦为3 （1×2+1=3）

注：结点间距离的定义：由结点向根方向（上行方向）时的边数×2，

与由根向叶结点方向（下行方向）时的边数之和。

输入输出格式

输入格式：

输入文件第一行为一个整数n(1≤n≤100)，表示二叉树结点个数。接下来的n-1行，表示从结点x到结点y（约定根结点为1），最后一行两个整数u、v，表示求从结点u到结点v的距离。

输出格式：

三个数，每个数占一行，依次表示给定二叉树的深度、宽度及结点u到结点v间距离。

输入输出样例

输入样例#1： 复制

10                                
1 2                            
1 3                            
2 4
2 5
3 6
3 7
5 8
5 9
6 10
8 6

输出样例#1： 复制

4
4
8

题解：LCA嘤嘤嘤

#include<bits/stdc++.h>
using namespace std;
int n;
struct edge{
    int to,next,val;
}G[100010];
int tot;
int maxn=0;
int depth[100010];
int st[100010][25];
int dist[100010];
bool used[100010];
int head[100010];
inline void addedge(int a,int b)
{
    G[tot].to=b;
    G[tot].next=head[a];
    G[tot].val=1;
    head[a]=tot++;
} 
void clear()
  {
       memset(used,false,sizeof(used));
       memset(head,-1,sizeof(head));
       memset(depth,0,sizeof(depth));
  }
  inline void tree(int s)
  {
      used[s]=1;
      for(int i=head[s];~i;i=G[i].next)
{
     int tt=G[i].to;
     if(used[tt])
     continue;
     dist[tt]=dist[s]+G[i].val;
      depth[tt]=depth[s]+1;
      maxn=max(depth[tt],maxn);
      st[tt][0]=s;
      for(int j=1;j<=20;j++)
      st[tt][j]=st[st[tt][j-1]][j-1];
      tree(tt);
}
   } 
int lca(int a,int b)
   {
        if(depth[a]>depth[b])
        swap(a,b);
        int d=depth[b]-depth[a];
         for(int i=0;(1<<i)<=d;i++)
          {
              if((1<<i)&d)
              b=st[b][i];
          }
          if(a==b)
          return a;
          for(int i=20;i>=0;i--)
           {
               if(st[a][i]!=st[b][i])
               {
                   a=st[a][i];
                   b=st[b][i];
               }
           }
           return st[a][0];
    } 
    int p,q;
int main()
{
    clear();
    scanf("%d",&n);
     for(int i=1;i<n;i++)
     {
          int a,b;
          scanf("%d %d",&a,&b);
           addedge(a,b);
      addedge(b,a);
      }
      scanf("%d %d",&p,&q);
      depth[1]=1;
      dist[1]=0;
      tree(1);
    printf("%d
",maxn);
    int wide=0;
     for(int i=1;i<=maxn;i++)
     {
         int ans=0;
         int t=i;
          for(int j=1;j<=n;j++)
          {
              if(depth[j]==t)
               ans++;
          }
          wide=max(ans,wide);
     }
     // printf("%d %d
",dist[p],dist[q]);
    // printf("%d %d %d",dist[p],dist[q],dist[lca(p,q)]);
      printf("%d
%d",wide,2*(dist[p]-dist[lca(p,q)])+dist[q]-dist[lca(p,q)]);
}