介绍完平面上凸包各种求取方法后,讲解三维顶点集合凸包的方法。
过程:
3DConvexHull( int argc, char *argv[] )
{
ReadVertices(); //读取所有顶点
DoubleTriangle(); //构造初始三角形
ConstructHull(); //构建三维顶点集合的凸包
}

//首先找到3个不共线的顶点,以相反的顺序建成三角形的两个面。接着找到不在三角面上的第四个顶点。在三角面上以逆时针顺序存储顶点,建立到新顶点的3个面。
void DoubleTriangle( void )
{
tVertex v0, v1, v2, v3, t;
tFace f0, f1 = NULL;
tEdge e0, e1, e2, s;
int vol;
v0 = vertices;
while ( Collinear( v0, v0->next, v0->next->next ) )//比较连续存储的3个顶点
if ( ( v0 = v0->next ) == vertices ) //提取下一个顶点
printf("所有顶点共线");
v1 = v0->next; //找到不共线的顶点
v2 = v1->next; //找到不共线的顶点
v0->mark = PROCESSED; //标记顶点处理过
v1->mark = PROCESSED; //标记顶点处理过
v2->mark = PROCESSED; //标记顶点处理过
f0 = MakeFace( v0, v1, v2, f1 );
f1 = MakeFace( v2, v1, v0, f0 );//以相反的顶点顺序构建第二个面
f0->edge[0]->adjface[1] = f1;
f0->edge[1]->adjface[1] = f1;
f0->edge[2]->adjface[1] = f1; //指出面的邻接面
f1->edge[0]->adjface[1] = f0;
f1->edge[1]->adjface[1] = f0;
f1->edge[2]->adjface[1] = f0; //指出面的邻接面
//准备找到不在面上的第四个顶点来构建体
v3 = v2->next;
vol = VolumeSign( f0, v3 ); //通过计算体积来判断是否第四个顶点不在面上
while ( !vol ) { //当体积为0的话,继续循环
if ( ( v3 = v3->next ) == v0 )
printf("所有顶点是共面的");
vol = VolumeSign( f0, v3 );
}
vertices = v3; //记录V3为现在被增加的顶点
}
//每次考察一个顶点,如果构成凸包中新顶点,则新建面和边,如处在现阶段的凸包之内,则不作其他处理;
void ConstructHull( void )
{
tVertex v, vnext;
int vol;
bool changed;
v = vertices;
do {
vnext = v->next; //取下一个顶点来处理
if ( !v->mark ) { //如果此顶点的标记为“还从未处理过”
v->mark = PROCESSED;//将此顶点标记为“已经被处理过”
changed = AddOne( v );//将新顶点加入,处在现凸包内,或构成新凸包的一个顶点
CleanUp( &vnext );
}
v = vnext;
} while ( v != vertices );
}
通过体积来计算此顶点与其他面的关系,若构成的体都为凹,则不予考虑。否则,可说此顶点位于某些面之外。若从此顶点能观察到某边的两个邻接面,则此边将被删除。若从此顶点只能观察到一个面,则将创建新面。
bool AddOne( tVertex p )
{
tFace f;
tEdge e, temp;
int vol;
bool vis = FALSE;
f = faces;
do {
vol = VolumeSign( f, p ); //计算每个面和新增加的顶点构成的锥体的体积
if ( vol < 0 ) {
f->visible = VISIBLE; //此面被标记为可见
vis = TRUE; //标识顶点已处于面之外
}
f = f->next; //取得下一个面
} while ( f != faces ); //对所有面循环处理
if ( !vis ) { //没有一个面可见,则顶点位于体内,不将作为凸包顶点
p->onhull = !ONHULL; //顶点作标记
return FALSE;
}
e = edges;
do {
temp = e->next; //取下一条边
if ( e->adjface[0]->visible && e->adjface[1]->visible )
e->delete = REMOVED;//如果这条边的两个邻接面都可见,则标记为删除此条边
else if ( e->adjface[0]->visible || e->adjface[1]->visible )
e->newface = MakeConeFace( e, p ); //构建新面
e = temp;
} while ( e != edges ); //所有边循环处理
return TRUE;
}
//计算体积,此结果的正负可判断顶点与面的“可见”关系。
int VolumeSign( tFace f, tVertex p )
{
double vol;
int voli;
double ax, ay, az, bx, by, bz, cx, cy, cz;
ax = f->vertex[0]->v[X] - p->v[X];
ay = f->vertex[0]->v[Y] - p->v[Y];
az = f->vertex[0]->v[Z] - p->v[Z]; //顶点坐标相减构成向量
bx = f->vertex[1]->v[X] - p->v[X];
by = f->vertex[1]->v[Y] - p->v[Y];
bz = f->vertex[1]->v[Z] - p->v[Z];
cx = f->vertex[2]->v[X] - p->v[X];
cy = f->vertex[2]->v[Y] - p->v[Y];
cz = f->vertex[2]->v[Z] - p->v[Z];
vol = ax * (by*cz - bz*cy)
+ ay * (bz*cx - bx*cz)
+ az * (bx*cy - by*cx);
//体积计算是通过法向量与一条边向量的点乘,因为点乘结果表示两个模与向量夹角的余弦,其中法向量的模是三角面上两条边的模乘上夹角的正弦,即为面积。而剩下的那个模乘上夹角的余弦,即为高。
return vol;
}
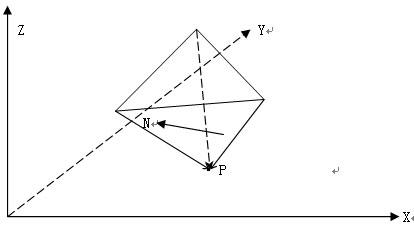
当一条边的一个邻接面对新加入的顶点是“可见”的时候,构建一个新面和两条新边
tFace MakeConeFace( tEdge e, tVertex p )
{
tEdge new_edge[2];
tFace new_face;
int i, j;
//准备构建两条新边
for ( i=0; i < 2; ++i )
//如果新边已经被创建过,直接拷贝过来即可
if ( !( new_edge[i] = e->endpts[i]->duplicate) ) {
//如果新边没有被创建过,则构建
new_edge[i] = MakeNullEdge();
new_edge[i]->endpts[0] = e->endpts[i];
new_edge[i]->endpts[1] = p;
e->endpts[i]->duplicate = new_edge[i];// 顶点标记这条新边
}
//创建新的面
new_face = MakeNullFace();
new_face->edge[0] = e; //构成面的原来那条边
new_face->edge[1] = new_edge[0];//构成面的第一条新边
new_face->edge[2] = new_edge[1]; //构成面的第二条新边
MakeCcw( new_face, e, p ); //以逆时针方向建立面上的顶点顺序
//将新建立的边和面联系起来
for ( i=0; i < 2; ++i )
for ( j=0; j < 2; ++j )
if ( !new_edge[i]->adjface[j] ) {
new_edge[i]->adjface[j] = new_face;
break; //新边和新面一旦联系,就跳出循环
}
return new_face;//处理结束,返回新建立的面
}