算法——二叉树

定义：

二叉树（Binary Tree）是n（n>=0）个节点的有限集合，该集合或者空集（称为空二叉树），或者由一个根节点和两棵互不相交的，分别称为根节点的左子树和右子树的二叉树组成。

特点：

• 每个结点最多有两棵子树，所以二叉树中不存在度大于2的结点。注意不是只有两棵子树，而是最多有。没有子树或者有一棵子树都是可以的。
• 左子树和右子树是有顺序的，次序不能任意颠倒。就像人是双手、双脚，但显然左手、左脚和右手、右脚是不一样的，右手戴左手套、右脚穿左鞋都会极其别扭和难受。
• 即使树中某结点只有一棵子树，也要区分它是左子树还是右子树。

二叉树的五种形态：

1. 空二叉树
2. 只有一个根节点
3. 根节点只有左子树
4. 根节点只有右子树
5. 根节点既有左子树又有右子树

特殊二叉树：

• 斜树：所有的节点都只有左子树的二叉树叫做左斜树，所有的节点都只有右子树的二叉树叫做右斜树。这两者统称为斜树。
• 满二叉树：在一棵二叉树中，如果所有分支节点都存在左子树和右子树，并且所有叶子都在同一层，这样的二叉树称为满二叉树
• 完全二叉树：对一棵具有n个结点的二叉树按层序编号，如果编号为i （1<=i<=n）的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同，则这棵二叉树称为完全二叉树。

二叉树性质：

• 性质1：在二叉树的第i层上至多有2^(i-1)个节点（i>=1）
• 性质2：深度为k的二叉树至多有2^k-1个节点（k>=1）
• 性质3：对任何一棵二叉树T，如果其终端节点数为n0，度为2的节点数为n2，则n0=n2+1

二叉树遍历：

二叉树的遍历（ traversing binary tree ）是指从根结点出发，按照某种次序依次访问二叉树中所有结点，使得每个结点被访问一次且仅被访问一次。

二叉树遍历方法：

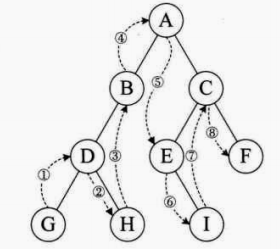
• 前序遍历：规则是若二叉树为空，则空操作返回，否则先访问根结点，然后前序遍历左子树，再前序遍历右子树。如图所示，遍历的顺序为：ABDGHCEIF。

• 中序遍历：规则是若树为空，则空操作返回，否则从根结点开始（注意并不是先访问根结点），中序遍历根结点的左子树，然后是访问根结点，最后中序遍历右子树。如图所示，遍历的顺序为：GDHBAEICF。

• 后序遍历：规则是若树为空，则空操作返回，否则从左到右先叶子后结点的方式遍历访向左右子树，最后是访问根结点。如图所示，遍历的顺序为：GHDBIEFCA。

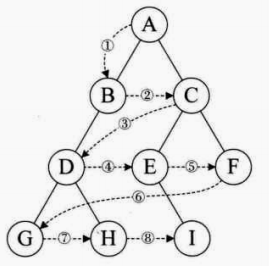
• 层序遍历：规则是若树为空，则空操作返回，否则从树的第一层， 也就是根结点开始访问，从上而下逐层遍历，在同一层中，按从左到右的顺序对结点逐个访问。如图所示，遍历的顺序为：ABCDEFGHI。

二叉搜索树的实现：

定义：

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树。如下图所示：

代码如下：

二叉树的节点类：

/**
 * 	二叉树的结点类
 * @author wydream
 *
 */

public class Node {

	int data;//节点数据
	Node leftChild;//左子节点的引用
	Node rightChild;//右子节点的引用
	boolean isDelete;//表示节点是否被删除
	
	public Node(int data) {
		this.data=data;
	}
	
	//打印节点内容
	public void display() {
		System.out.println(data);
	}
	
}

　　

二叉树的接口：

/**
 * 	二叉树的具体方法
 * @author wydream
 *
 */

public interface Tree {

	//查找节点
    public Node find(int key);
    //插入新节点
    public boolean insert(int data);
     
    //中序遍历
    public void infixOrder(Node current);
    //前序遍历
    public void preOrder(Node current);
    //后序遍历
    public void postOrder(Node current);
     
    //查找最大值
    public Node findMax();
    //查找最小值
    public Node findMin();
     
    //删除节点
    public boolean delete(int key);	
}

　　

二叉树的具体实现：

import org.junit.jupiter.api.Test;

public class BinaryTree implements Tree {
	
	private Node root;//根节点

	@Override
	public Node find(int key) {
		Node current=root;
		while(current!=null) {
			if(current.data>key) {//当前值比查找值大，搜索左子树
				current=current.leftChild;
			}else if(current.data<key) {//当前值比查找值小，搜索右子树
				current=current.rightChild;
			}else {
				return current;
			}
		}
		return null;//遍历完整个树没找到，返回null
	}

	@Override
	public boolean insert(int key) {
		
		Node newNode=new Node(key);
		if(root==null) {//当前树为空树，没有任何节点
			root=newNode;
			return true;
		}else {
			Node current=root;
			Node parentNode=null;
			while(current!=null) {
				parentNode=current;
				if(current.data>key) {//当前值比插入值大，搜索左子节点
					current=current.leftChild;
					if(current==null) {//左孩子为空，则插入该节点到左孩子
						parentNode.leftChild=newNode;
						return true;
					}
				}else {//当前值比插入值小，搜索右子节点
					current=current.rightChild;
					if(current==null) {//右孩子为空，则插入该节点到右孩子
						parentNode.rightChild=newNode;
						return true;
					}
				}
			}
		}
		return false;
	}

	//删除节点
	@Override
	public boolean delete(int key) {
		Node current=root;
		Node parent=root;
		boolean isLeftChild=false;
		//查找删除值，找不到直接返回false
		while(current.data!=key) {
			parent=current;
			if(current.data>key) {
				isLeftChild=true;
				current=current.leftChild;
			}else {
				isLeftChild=false;
				current=current.rightChild;
			}
			if(current==null) {
				return false;
			}
		}
		
		//如果当前节点没有子节点
		if(current.leftChild==null&&current.rightChild==null) {
			if(current==root) {
				root=null;
			}else if(isLeftChild) {
				parent.leftChild=null;
			}else {
				parent.rightChild=null;
			}
			return true;
		}else if(current.leftChild==null&&current.rightChild!=null){//当前节点有一个子节点，右子节点
			if(current==root) {
				root=current.rightChild;
			}else if(isLeftChild) {
				parent.leftChild=current.rightChild;
			}else {
				parent.rightChild=current.rightChild;
			}
			return true;
		}else if(current.rightChild==null&&current.leftChild!=null) {//当前节点有一个子节点，左子节点
			if(current==root) {
				root=current.leftChild;
			}else if(isLeftChild) {
				parent.leftChild=current.leftChild;
			}else {
				parent.rightChild=current.leftChild;
			}
			return true;
		}else {//当前节点存在两个子节点
			Node successor = getSuccessor(current);
            if(current == root){
                root= successor;
            }else if(isLeftChild){
                parent.leftChild = successor;
            }else{
                parent.rightChild = successor;
            }
            successor.leftChild = current.leftChild;
		}
		
		
		return false;
	}
	
	//中序遍历:左子树——》根节点——》右子树
	public void infixOrder(Node current) {
		if(current!=null) {
			infixOrder(current.leftChild);
			System.out.println(current.data);
			infixOrder(current.rightChild);
		}
	}
	
	//前序遍历:根节点——》左子树——》右子树
	public void preOrder(Node current) {
		if(current!=null) {
			System.out.println(current.data);
			preOrder(current.leftChild);
			preOrder(current.rightChild);
		}
	}
	

	//后序遍历:左子树——》右子树——》根节点
	public void postOrder(Node current) {
		if(current!=null) {
			postOrder(current.leftChild);
			postOrder(current.rightChild);
			System.out.println(current.data);
		}
	}
	
	//查找最小值
	public Node findMin() {
		Node current=root;
		Node minNode=current;
		while(current!=null) {
			minNode=current;
			current=current.leftChild;
		}
		return minNode;
	}
	
	
	//查找最大值
	public Node findMax() {
		Node current=root;
		Node maxNode=current;
		while(current!=null) {
			maxNode=current;
			current=current.rightChild;
		}
		return maxNode;
	}
	
	public Node getSuccessor(Node delNode) {
		Node successorParent=delNode;
		Node successor=delNode;
		Node current=delNode.rightChild;
		while(current!=null) {
			successorParent=successor;
			successor=current;
			current=current.leftChild;
		}
		//后继节点不是删除节点的右子节点,将后继节点替换删除节点
		if(successor!=delNode.rightChild) {
			successorParent.leftChild=successor.rightChild;
			successor.rightChild=delNode.rightChild;
		}
		return successor;
	}
	
	//测试
	@Test
	public void test() {
		BinaryTree bt = new BinaryTree();
        bt.insert(50);
        bt.insert(20);
        bt.insert(80);
        bt.insert(10);
        bt.insert(30);
        bt.insert(60);
        bt.insert(90);
        bt.insert(25);
        bt.insert(85);
        bt.insert(100);
        bt.delete(10);//删除没有子节点的节点
        bt.delete(30);//删除有一个子节点的节点
        bt.delete(80);//删除有两个子节点的节点
        System.out.println(bt.findMax().data);
        System.out.println(bt.findMin().data);
        System.out.println(bt.find(100));
        System.out.println(bt.find(200));
        System.out.println("=====中序遍历=====");
		infixOrder(bt.root);
		System.out.println("=====前序遍历=====");
		preOrder(bt.root);
		System.out.println("=====后序遍历=====");
		postOrder(bt.root);
		
	}
	
}

　　

测试结果：

100
20
com.alibaba.test11.tree.Node@ed7f8b4
null
=====中序遍历=====
20
25
50
60
85
90
100
=====前序遍历=====
50
20
25
85
60
90
100
=====后序遍历=====
25
20
60
100
90
85
50

　　

本博客代码参考：https://www.cnblogs.com/ysocean/p/8032642.html#_label9