一、什么是子字符串查找
子字符串查找是一种基本的字符串操作,是给定一段长度为N的文本和一个长度为M的模式(pattern)字符串,在文本中找到一个和该模式相符的子字符串的操作;
在实际的应用场景中,模式相对文本来说是很短的,即M远小于N,我们一般也会对模式进行预处理来支持在文本中的快速查找。
二、测试环境及基础类
开发语言使用的是C#;
StringSearcher基础的基类,负责加载文件内容、字符串查找、性能测试等;
public abstract class StringSearcher
{
public string[] Lines { get; set; }
public StringSearcher(string textFile)
{
Lines = GetFileContent(textFile);
}
protected virtual string[] GetFileContent(string textFile)
{
var lines = File.ReadAllLines(textFile);
return lines;
}
public abstract IEnumerable<Match> IndexOf(string pattern);
public virtual void Print(IEnumerable<Match> matches)
{
foreach (var m in matches)
{
m.Print();
}
}
public void PerfTest(int testNumber, string pattern)
{
Console.WriteLine($"we will execute {testNumber} times.");
Stopwatch watch = new Stopwatch();
watch.Start();
for (int i = 0; i < testNumber; i++)
{
this.IndexOf(pattern);
}
watch.Stop();
Console.WriteLine($"execute total time is {watch.ElapsedMilliseconds} ms");
}
}
Match类负责记录字符串搜索的匹配信息,以便输出搜索结果;
public class Match
{
public int NO { get; set; }
public int Start { get; set; }
public int Lenght { get; set; }
public string Line { get; set; }
public void Print()
{
Console.WriteLine($"Line {NO}, start {Start}");
}
}
三、暴力子字符串查找算法
所谓暴力查找算法就是使用文本中的字符逐个的跟模式进行比较,如果不匹配则直接从下一个文本字符重新开始比较;
public class BruteForceStringSearcher : StringSearcher
{
public BruteForceStringSearcher(string filePath):base(filePath)
{ }
public override IEnumerable<Match> IndexOf(string pattern)
{
List<Match> result = new List<Match>();
int pLen = pattern.Length;
for (var lNO =0; lNO<Lines.Length; lNO ++)
{
string line = Lines[lNO];
int lLen = line.Length;
for (int i = 0; i < lLen - pLen; i++)
{
int j = 0;
for (; j < pLen; j++)
{
if (line[i + j] != pattern[j])
{
break;
}
}
if (j == pLen)
{
var m = new Match {
NO= lNO,
Line = line,
Start = i,
Lenght = pLen
};
result.Add(m);
break;
}
}
}
return result;
}
}
从暴力子串查找算法的实现来看,文本串除了最后的N个字符之外,每个文本字符都会进行N的比较,所以时间复杂度是(M-N)*N;
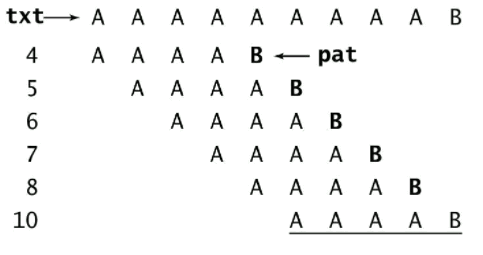
从下图我们可以看到暴力子字符串查找算法最坏的情况,只有文本串和模式串存在大部分重复字符的特殊情况下才会出现;但是从自然语言的实际使用场景来看,基本上不会出现这种情况,更多的时候是模式串很短,绝大多数比较会在比较第一个字符的时候就会产生不匹配,所以时间复杂度可以粗略的算作跟文本串的长度成正比;
进行简单的测试
var searcher = new BruteForceStringSearcher("txt");
var result = searcher.IndexOf("async");
searcher.Print(result);
searcher.PerfTest(10000, "async");
//Line 0, start 39
//Line 2, start 59
//Line 4, start 53
//Line 5, start 94
//Line 6, start 18
//Line 7, start 44
//we will execute 10000 times.
//execute total time is 50 ms
四、KMP子字符串查找算法
针对暴力算法的最坏情况进行分析,我们已经知晓了文本串的一些信息,而这些信息其实跟模式串的当前前缀是相同的,如果我们针对模式串进行一些预处理的话,其实是可以避免这种情况下的文本串指针的回退的;
这个算法就是KMP算法,是由Knuth、Morris、Pratt共同提出的模式匹配算法;
通过下图我们可以看到KMP算法的思想的原理;
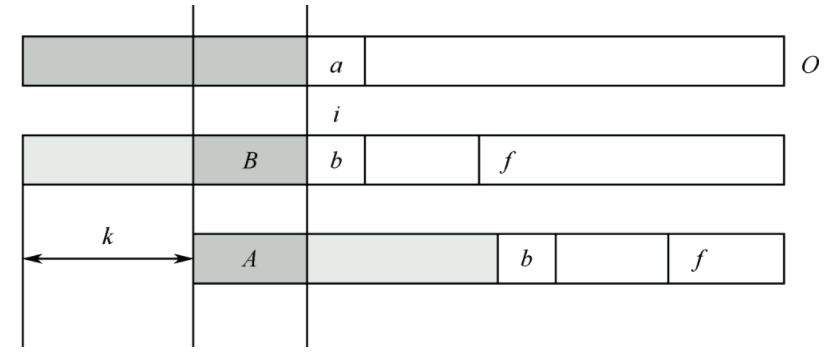
在位置i处,我们的文本串的字符是a,模式串的字符是b,很显然两者不相等了;
由于已经匹配的前缀模式串中存在两个相等的子模式串A和B,所以可以直接移动整个模式串,直至A占用B的位置,然后将A后边的字符跟a进行比较,从而避免了i指针的回退;
这里需要强调的几个关键点是
模式串的前i-1个字符与文本串是匹配的;
A是这个i-1为的子模式串的最大前缀公共子串;
B是这个i-1为的子模式串的最后前缀公共子串;
A和B串是从左到右每个对应的字符相等;
模式串移动的长度是i-1-最大公共子串的长度;
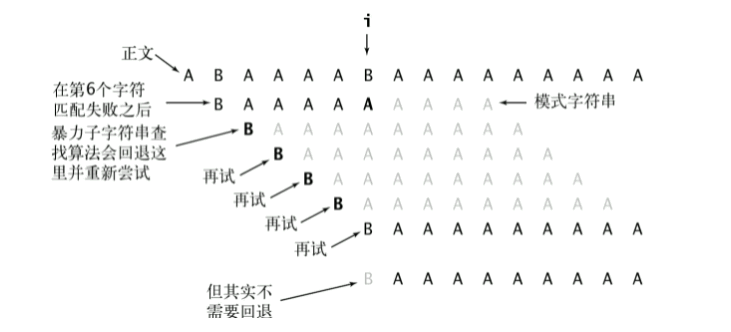
还是针对暴力破解最坏的情况,由于BAAAA不存在最大公共子串,所以直接将模式串右移5-0=5个位置,则直接跳过文本串中4次比较计算;
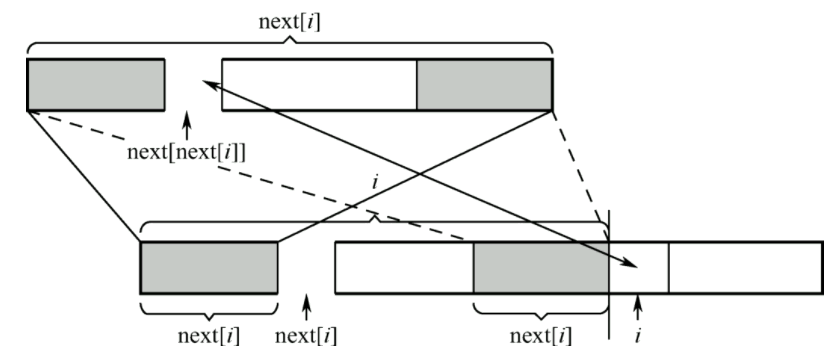
通过KMP算法的原理的了解,算法的关键是对模式串的每个字符的最大公共子串的长度;我们使用next数组来承载这个最大公共子串的长度;
next数组的值是一个具体的数值,表示最大公共子串的长度;
对于next数组的计算,当前字符的结果是依赖上一个字符的结果的;
我们需要比较两个公共子串A和B右侧的元素是否相等
如果相等则直接将上一个字符的结果=1保存即可;
如果不相等,则需要找到A的次一级最长公共子串A',然后计算A'和B右侧的元素是否相等,如果相等则将A'的结果=1保存即可;如果不等则进行递归操作即可;
根据以上讨论,我们实现了KMPStringSearcher
public class KMPStringSearcher : StringSearcher
{
Dictionary<string, List<int>> nexts = new Dictionary<string, List<int>>();
public KMPStringSearcher(string filePath):base(filePath)
{ }
List<int> GetNext(string pattern)
{
if (!nexts.ContainsKey(pattern))
{
List<int> next = new List<int>();
nexts.Add(pattern, next);
InitNext(pattern, next);
}
return nexts[pattern];
}
void InitNext(string pattern, List<int> next)
{
next.Add( -1);
for (int i = 1; i < pattern.Length; i++)
{
int j = next[i - 1];
if (pattern[j + 1] != pattern[i] && j >= 0)
{
j = next[j];
}
if (pattern[j + 1] == pattern[i])
{
next.Add(j+1);
}
else
{
next.Add(-1);
}
}
}
public override IEnumerable<Match> IndexOf(string pattern)
{
List<Match> result = new List<Match>();
var next = GetNext(pattern);
int pLen = pattern.Length;
for (var lNO =0; lNO<Lines.Length; lNO ++)
{
string line = Lines[lNO];
int lLen = line.Length;
int j = 0;
for (int i = 0; i < lLen - pLen; )
{
for (; j < pLen; j++, i++)
{
if (line[i] != pattern[j])
{
if (j != 0)
{
j = next[j - 1] + 1;
}
else
{
i++;
}
break;
}
}
if (j == pLen)
{
var m = new Match {
NO= lNO,
Line = line,
Start = i - pLen,
Lenght = pLen
};
result.Add(m);
break;
}
}
}
return result;
}
}
对相同的数据进行测试,从测试结果可以看到,虽然KMP算法通过一个O(m)的预处理,使匹配的复杂度降为O(n+m),但是KMP算法的这个理论成果并不能为最坏情况的线性级别运行时间做保证。在实际应用中,它比暴力算法的速度优势并不十分明显,因为极少有应用程序需要在重复性很高的文本中查找重复性很高的模式。
var searcher = new KMPStringSearcher("txt");
var result = searcher.IndexOf("async");
searcher.Print(result);
searcher.PerfTest(10000, "async");
//Line 0, start 39
//Line 2, start 59
//Line 4, start 53
//Line 5, start 94
//Line 6, start 18
//Line 7, start 44
//we will execute 10000 times.
//execute total time is 64 ms