具体原理网址:http://wenku.baidu.com/link?url=zSDn1fRKXlfafc_tbofxw1mTaY0LgtH4GWHqs5rl8w2l5I4GF35PmiO43Cnz3YeFrrkGsXgnFmqoKGGaCrylnBgx4cZC3vymiRYvC4d3DF3
自组织特征映射神经网络(Self-Organizing Feature Map。也称Kohonen映射),简称为SMO网络,主要用于解决模式识别类的问题。SMO网络属于无监督学习算法,与之前的Kmeans算法类似。所不同的是,SMO网络不需要预先提供聚类的数量,类别的数量是由网络自动识别出来的。
基本思想:将距离小的集合划分为同一类别,而将距离大的个体集合划分为不同的类别。
6.4.1 SMO网络框架
SMO网络比较简单,只有输入层和输出层。
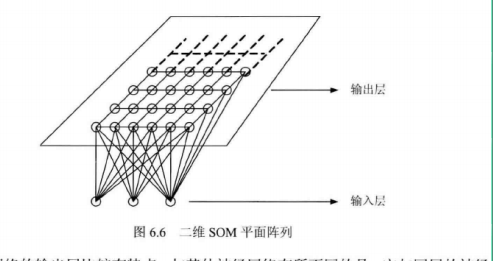
SMO网络的输出层比较有特点,与其他神经网络有所不同的是,它与同层的神经元之间建立侧向连接,并可通过权值的学习形成特定的模式。输出层排列成棋盘的形状。输出层的神经元可以形成多种形式,不同的形式可以映射出不同的模式,如一维线阵、二维平面阵和三维的栅格等。对于二维的训练数据,排列一般是二维平面阵。
实现步骤:
1.输入层网络
输入层网络节点和数据集同行数、同列数,但数据集要归一化。
2.输出网络
一般根据数据集的维度来构建输出网络。例如二维的情况,希望分为4类,输出层可设计为4*2的矩阵
3.权重节点
根据输入层的数据集的维度和输出层的预估分类数,定义权重节点的维度。例如,数据集是二维的,权重的行数就定为2,分4类,权重列数就选4.权重值一般给定一个0~1之间的随机值。
4.定义学习率
学习率会影响收敛的速度,可以定义一个动态的学习函数,随着迭代的次数增加而收敛。本例中的学习函数为:
式中,maxLrate为最大学习率,minLrate为最小学习率,MaxIteration为最大迭代次数,i为当前迭代次数。
5.定义聚类半径函数
学习半径影响聚类的效果。可以定义一个动态的收缩半径函数,随着迭代次数的增加而收缩,本例中定义的半径函数:
数、式中,maxR为最大聚类半径,minR为最小聚类半径,MaxItertion为最大的迭代次数,i为当前迭代的次数。
6.聚类的过程:
- 接受输入:首先计算本次迭代的学习率和学习半径,并且从训练集中随机选取一个样本
- 寻找获胜节点:计算数据集中其他样本与此样本的距离,从中找到点积最小的获胜节点
- 计算优胜邻域:根据这两个节点计算出聚类的邻域,并找出此邻域中所有节点。
- 调整权值:根据学习率、样本数据调整权重。
- 根据计算的结果,为数据集分配类别标签。
- 评估结果:SMO网络属于无监督聚类,输出的结果就是聚类后的标签,如果训练集已经被分类好了,即具有分类标签,那么通过新旧标签的比较就可以反映聚类结果的准确度。
6.4.2 SOM类
初始构造方法:
class Kohonen(object): def __init__(self): self.lratemax = 0.8 #最大学习率--欧式距离 self.lratemin = 0.05 #最小学习率--欧式距离 self.rmax = 5.0 #最大聚类半径--根据数据集 self.rmin = 0.5 #最小聚类半径--根据数据集 self.Steps = 1000 #迭代次数 self.lratelist = [] #学习率收敛曲线 self.rlist = [] #学习半径收敛曲线 self.w = [] #权重向量组 self.M = 2 #M*N聚类的总数 self.N = 2 #M/N表示邻域的参数 self.dataMat = [] #外部导入数据集 self.classLabel = [] #聚类后的类别标签
6.4.3 功能函数
(1)数据归一化
def normlize(self,dataMat): #数据标准化归一化 [m,n] = shape(dataMat) for i in xrange(n-1): dataMat[:,i] = (dataMat[:,i]-mean(dataMat[:,i]))/(std(dataMat[:,i])+1.0e-10) return dataMat
(2)计算欧氏距离:
def distEclud(vecA,vecB): #欧式距离 eps = 1.0e-6 return linalg.norm(vecA-vecB) + eps
(3)加载数据文件
def loadDataSet(self,filename): #加载数据集 numFeat = len(open(filename).readline().split(' '))-1 fr = open(filename) for line in fr.readlines(): lineArr = [] curLine = line.strip().split(' ') lineArr.append(float(curLine[0])) lineArr.append(float(curLine[1])) self.dataMat.append(lineArr) self.dataMat = mat(self.dataMat)
(4)初始化第二层网格
#coding:utf-8 from numpy import * class Kohonen(object): def __init__(self): self.lratemax = 0.8 #最大学习率--欧式距离 self.lratemin = 0.05 #最小学习率--欧式距离 self.rmax = 5.0 #最大聚类半径--根据数据集 self.rmin = 0.5 #最小聚类半径--根据数据集 self.Steps = 1000 #迭代次数 self.lratelist = [] #学习率收敛曲线 self.rlist = [] #学习半径收敛曲线 self.w = [] #权重向量组 self.M = 2 #M*N聚类的总数 self.N = 2 #M/N表示邻域的参数 self.dataMat = [] #外部导入数据集 self.classLabel = [] #聚类后的类别标签 def ratecalc(self,i): #学习率和半径 Learn_rate = self.lratemax-((i+1.0)*(self.lratemax-self.lratemin))/self.Steps R_rate = self.rmax-((i+1.0)*(self.rmax-self.rmin))/self.Steps return Learn_rate,R_rate def normlize(self,dataMat): #数据标准化归一化 [m,n] = shape(dataMat) for i in xrange(n-1): dataMat[:,i] = (dataMat[:,i]-mean(dataMat[:,i]))/(std(dataMat[:,i])+1.0e-10) return dataMat def distEclud(self,vecA,vecB): #欧式距离 eps = 1.0e-6 data = vecA-vecB data = linalg.norm(vecA-vecB) + eps return linalg.norm(vecA-vecB) + eps def loadDataSet(self,filename): #加载数据集 numFeat = len(open(filename).readline().split(' '))-1 fr = open(filename) for line in fr.readlines(): lineArr = [] curLine = line.strip().split(' ') lineArr.append(float(curLine[0])) lineArr.append(float(curLine[1])) self.dataMat.append(lineArr) self.dataMat = mat(self.dataMat) def init_grid(self): k = 0 #构建第二层网络模型 grid = mat(zeros((self.M*self.N,2))) for i in xrange(self.M): for j in xrange(self.N): grid[k,:] = [i,j] k += 1 return grid def train(self): dm,dn = shape(self.dataMat) #1.构建输入网络 normDataset = self.normlize(self.dataMat) #归一化数据 grid = self.init_grid() #初始化第二层分类器 self.w = random.rand(self.M*self.N,dn)#3.随机初始化两层之间的权重值 # distM = self.distEclud #确定距离公式 #4.迭代求解 if self.Steps < 5*dm: self.Steps = 5*dm #设定最小迭代次数 for i in xrange(self.Steps): lrate,r = self.ratecalc(i) #1)计算当前迭代次数下的学习率和分类半径 self.lratelist.append(lrate) self.rlist.append(r) #2)随机生成样本索引,并抽取一个样本 k = random.randint(0,dm) mySample = normDataset[k,:] #3)计算最优节点:返回最小距离的索引值 minIndx =[self.distEclud (mySample,i) for i in self.w] minIndx = minIndx.index(min(minIndx)) # self.w[minIndx,:] = self.w[minIndx,:]+lrate*(mySample[0]-self.w[minIndx,:]) #4)计算邻域 d1 = ceil(minIndx/self.M) #计算此节点在第二层矩阵中的位置 d2 = mod(minIndx,self.M) distMat = [self.distEclud(mat([d1,d2]),i) for i in grid] nodelindx = (array(distMat) < r).nonzero() for j in xrange (shape(self.w)[1]): #5)按列更新权重 if sum(nodelindx == j): self.w[:,j] = self.w[:,j]+lrate*(mySample[0]-self.w[:,j]) #主循环结束 self.classLabel = range(dm) #分配和存储聚类后的类别标签 for i in xrange(dm): self.classLabel[i] = distM(normDataset[i,:],self.w).argmin() self.classLabel = mat(self.classLabel) SMOnet = Kohonen() SMOnet.loadDataSet('testSet2.txt') SMOnet.train()
资料来源:郑捷《机器学习算法原理与编程实践》 仅供学习研究