Kruskal算法(一)之 C语言详解

最小生成树

在含有n个顶点的连通图中选择n-1条边，构成一棵极小连通子图，并使该连通子图中n-1条边上权值之和达到最小，则称其为连通网的最小生成树。 

例如，对于如上图G4所示的连通网可以有多棵权值总和不相同的生成树。

克鲁斯卡尔算法介绍

克鲁斯卡尔(Kruskal)算法，是用来求加权连通图的最小生成树的算法。

基本思想：按照权值从小到大的顺序选择n-1条边，并保证这n-1条边不构成回路。 
具体做法：首先构造一个只含n个顶点的森林，然后依权值从小到大从连通网中选择边加入到森林中，并使森林中不产生回路，直至森林变成一棵树为止。

克鲁斯卡尔算法图解

以上图G4为例，来对克鲁斯卡尔进行演示(假设，用数组R保存最小生成树结果)。

第1步：将边<E,F>加入R中。 
    边<E,F>的权值最小，因此将它加入到最小生成树结果R中。 
第2步：将边<C,D>加入R中。 
    上一步操作之后，边<C,D>的权值最小，因此将它加入到最小生成树结果R中。 
第3步：将边<D,E>加入R中。 
    上一步操作之后，边<D,E>的权值最小，因此将它加入到最小生成树结果R中。 
第4步：将边<B,F>加入R中。 
    上一步操作之后，边<C,E>的权值最小，但<C,E>会和已有的边构成回路；因此，跳过边<C,E>。同理，跳过边<C,F>。将边<B,F>加入到最小生成树结果R中。 
第5步：将边<E,G>加入R中。 
    上一步操作之后，边<E,G>的权值最小，因此将它加入到最小生成树结果R中。 
第6步：将边<A,B>加入R中。 
    上一步操作之后，边<F,G>的权值最小，但<F,G>会和已有的边构成回路；因此，跳过边<F,G>。同理，跳过边<B,C>。将边<A,B>加入到最小生成树结果R中。

此时，最小生成树构造完成！它包括的边依次是：<E,F> <C,D> <D,E> <B,F> <E,G> <A,B>。

克鲁斯卡尔算法分析

根据前面介绍的克鲁斯卡尔算法的基本思想和做法，我们能够了解到，克鲁斯卡尔算法重点需要解决的以下两个问题： 
问题一 对图的所有边按照权值大小进行排序。 
问题二 将边添加到最小生成树中时，怎么样判断是否形成了回路。

问题一很好解决，采用排序算法进行排序即可。

问题二，处理方式是：记录顶点在"最小生成树"中的终点，顶点的终点是"在最小生成树中与它连通的最大顶点"(关于这一点，后面会通过图片给出说明)。然后每次需要将一条边添加到最小生存树时，判断该边的两个顶点的终点是否重合，重合的话则会构成回路。 以下图来进行说明：

在将<E,F> <C,D> <D,E>加入到最小生成树R中之后，这几条边的顶点就都有了终点：

(01) C的终点是F。 
(02) D的终点是F。 
(03) E的终点是F。 
(04) F的终点是F。

关于终点，就是将所有顶点按照从小到大的顺序排列好之后；某个顶点的终点就是"与它连通的最大顶点"。 因此，接下来，虽然<C,E>是权值最小的边。但是C和E的重点都是F，即它们的终点相同，因此，将<C,E>加入最小生成树的话，会形成回路。这就是判断回路的方式。

克鲁斯卡尔算法的代码说明

有了前面的算法分析之后，下面我们来查看具体代码。这里选取"邻接矩阵"进行说明，对于"邻接表"实现的图在后面的源码中会给出相应的源码。

1. 基本定义

// 邻接矩阵
typedef struct _graph
{
    char vexs[MAX];       // 顶点集合
    int vexnum;           // 顶点数
    int edgnum;           // 边数
    int matrix[MAX][MAX]; // 邻接矩阵
}Graph, *PGraph;

// 边的结构体
typedef struct _EdgeData
{
    char start; // 边的起点
    char end;   // 边的终点
    int weight; // 边的权重
}EData;

Graph是邻接矩阵对应的结构体。 
vexs用于保存顶点，vexnum是顶点数，edgnum是边数；matrix则是用于保存矩阵信息的二维数组。例如，matrix[i][j]=1，则表示"顶点i(即vexs[i])"和"顶点j(即vexs[j])"是邻接点；matrix[i][j]=0，则表示它们不是邻接点。 
EData是邻接矩阵边对应的结构体。

2. 克鲁斯卡尔算法

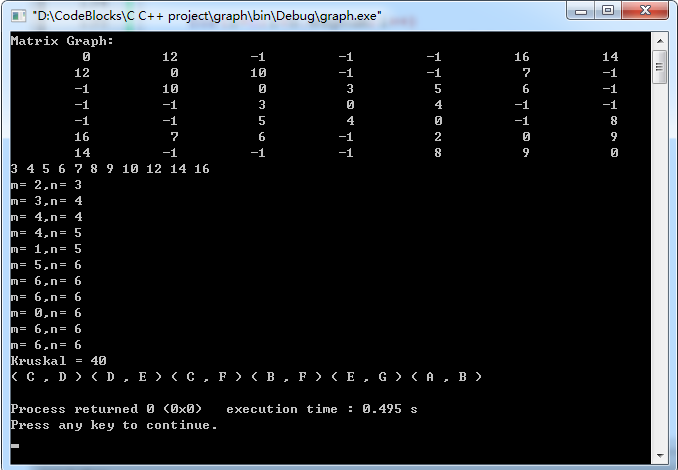
#include<stdio.h>
#include<stdlib.h>
#include<malloc.h>
#include<string.h>
#define MAX 100
#define INF -1
typedef struct Graph
{
    char vexs[MAX];
    int vexnum;
    int edgnum;
    int matrix[MAX][MAX];
}Graph,*PGraph;

typedef struct EdgeData
{
    char start;
    char end;
    int weight;
}EData;

static int get_position(Graph g,char ch)
{
    int i;
    for(i=0;i<g.vexnum;i++)
        if(g.vexs[i]==ch)
            return i;
    return -1;
}

Graph* create_graph()
{
    char vexs[]= {'A','B','C','D','E','F','G'};
    int matrix[][7]= {
        {0,12,INF,INF,INF,16,14},
        {12,0,10,INF,INF,7,INF},
        {INF,10,0,3,5,6,INF},
        {INF,INF,3,0,4,INF,INF},
        {INF,INF,5,4,0,INF,8},
        {16,7,6,INF,2,0,9},
        {14,INF,INF,INF,8,9,0}};
    int vlen=sizeof(vexs)/sizeof(vexs[0]);
    int i,j;
    Graph *pG;
    if((pG=(Graph*)malloc(sizeof(Graph)))==NULL)
        return NULL;
    memset(pG,0,sizeof(pG));
    pG->vexnum=vlen;
    for(i=0;i<pG->vexnum;i++)
        pG->vexs[i]=vexs[i];
    for(i=0;i<pG->vexnum;i++)
        for(j=0;j<pG->vexnum;j++)
            pG->matrix[i][j]=matrix[i][j];
    for(i=0;i<pG->vexnum;i++)
    {
        for(j=0;j<pG->vexnum;j++)
        {
            if(i!=j&&pG->matrix[i][j]!=INF)
                pG->edgnum++;
        }
    }
    pG->edgnum/=2;
    return pG;
}

void print_graph(Graph G)
{
    int i,j;
    printf("Matrix Graph: 
");
    for(i=0;i<G.vexnum;i++)
    {
        for(j=0;j<G.vexnum;j++)
            printf("%10d ",G.matrix[i][j]);
        printf("
");
    }
}

EData* get_edges(Graph G)
{
    EData *edges;
    edges=(EData*)malloc(G.edgnum*sizeof(EData));
    int i,j;
    int index=0;
    for(i=0;i<G.vexnum;i++)
    {
        for(j=i+1;j<G.vexnum;j++)
        {
            if(G.matrix[i][j]!=INF)
            {
                edges[index].start=G.vexs[i];
                edges[index].end=G.vexs[j];
                edges[index].weight=G.matrix[i][j];
                index++;
            }
        }
    }
    return edges;
}

void sort_edges(EData *edges,int elen)
{
    int i,j;
    for(i=0;i<elen;i++)
    {
        for(j=i+1;j<elen;j++)
        {
            if(edges[i].weight>edges[j].weight)
            {
                EData tmp=edges[i];
                edges[i]=edges[j];
                edges[j]=tmp;
            }
        }
    }
}

int get_end(int vends[],int i)
{
    while(vends[i]!=0)
        i=vends[i];
    return i;
}

void kruskal(Graph G)
{
    int i,m,n,p1,p2;
    int length;
    int index=0;
    int vends[MAX]={0};
    EData rets[MAX];
    EData *edges;
    edges=get_edges(G);
    sort_edges(edges,G.edgnum);

    for(i=0;i<G.edgnum;i++)
        printf("%d ",edges[i].weight);
    printf("
");
    for(i=0;i<G.edgnum;i++)
    {
        p1=get_position(G,edges[i].start);
        p2=get_position(G,edges[i].end);
        m=get_end(vends,p1);
        n=get_end(vends,p2);
        printf("m= %d,n= %d",m,n);
        if(m!=n)
        {
            vends[m]=n;
            rets[index++]=edges[i];
        }
    }
    free(edges);

    length=0;
    for(i=0;i<index;i++)
        length+=rets[i].weight;
    printf("Kruskal = %d
",length);
    for(i=0;i<index;i++)
        printf("( %c , %c ) ",rets[i].start,rets[i].end);
    printf("
");
}

int main()
{
    Graph *pG;
    pG=create_graph();
    print_graph(*pG);
    kruskal(*pG);
}

运行结果：