一. 树状数组简介:
树状数组用来求区间元素的和,求一次区间元素和的效率为O(log n).
二. 图解树状数组:
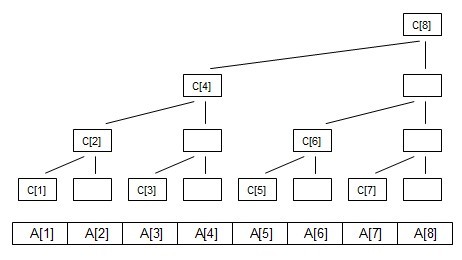
假设序列为:A[1]-A[8],C[]为树状数组.
C[1] = A[1];
C[2] = A[1] + A[2];
C[3] = A[3];
C[4] = A[1] + A[2] + A[3] + A[4];
C[5] = A[5];
C[6] = A[5] + A[6];
C[7] = A[7];
C[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8];
将十进制化成二进制,然后观察这些二进制数最右边的1的位置:
1 --> 00000001
2 --> 00000010
3 --> 00000011
4 --> 00000100
5 --> 00000101
6 --> 00000110
7 --> 00000111
8 --> 00001000
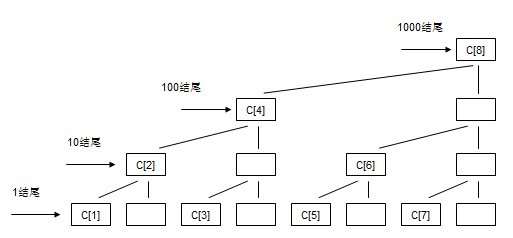
最右边的1的位置C[]的关系:
在满二叉树中,
以1结尾的节点(C[1], C[3], C[5], C[7]),其叶子数有1个,所以这些节点C[i]代表区间为1的元素和;
以10结尾的节点(C[2], C[6]),其叶子数为2,所以这些节点C[i]代表区间范围为2的元素和;
以100结尾的节点(C[4]),其叶子数为8个,锁业这些节点C[i]代表的区间范围为4的元素和;
以1000结尾的节点(C[8]),其椰子树为8,所以这些节点C[i]代表的区间范围为8的元素和.
扩展到一般情况:
i的二进制中的从右往左数有连续的x个"0",那么拥有2^x个叶子,为序列A[]中的第 i - 2^x +1 到第 i 个元素的和.
所以,C[i] = A[i-2^x+1] + ... + A[i],其中x为i的二进制中的从右往左数有连续"0"的个数.
void init() {
for (int i =1; i <= n; i++) {
int len = i&(-i);
while (len /= 2)
C[i] += C[i-len];
C[i] += A[i];
}
}
三. 利用树状数组求前i个元素的和S[i]:
C[i] = A[i - 2^x + 1] + ... + A[i];
int Sum(int i) {
int s = 0;
while (i > 0) {
s += C[i];
i -= i&(-i);
}
return s;
}
四. 更新C[]:
void Update(int i, int value) { //A[i]的改变值为value
while (i <= n) {
C[i] += value;
i += i &(-i);
}
}
Reference:
[1] http://www.cnblogs.com/justforgl/archive/2012/07/27/2612364.html