【牛客小白月赛27 A 巨木之森】
题意
给一棵n个结点的树,m块钱。定义从一个点出发遍历整棵树的花费是路径的边权和。
求最多能选择多少个不同的起点使得从这些起点分别遍历整棵树的花费<=m。
题解
首先,肯定的是用贪心的思想来做,假设现在已知从每个结点出发遍历整棵树的花费分别是多少,那么只需要把花费从小到大排序,从小到大取,取到不能取为止。
那么现在问题转化成为怎么求所有点作为起点遍历整棵树的花费。
首先考虑,给定一个起点,怎么求遍历整棵树的最小花费,对于每一个起点,我们势必是要最小化花费使得节省出更多的钱,希望供更多的起点使用。
那如何求最小花费呢。
考虑从一个起点出发,如果最后要求需要回到起点,那么显然花费是2*(整棵树的边权和),因为每条边都会一来一回走两遍。
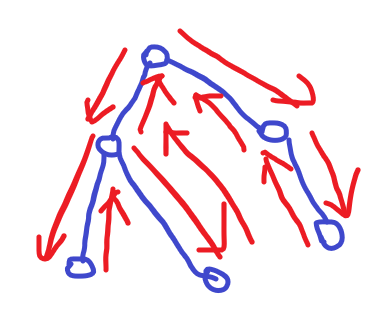
那么现在不需要回到起点,走到遍历的最后一个节点就停下了,那么跟上面的那种少了哪些花费呢?
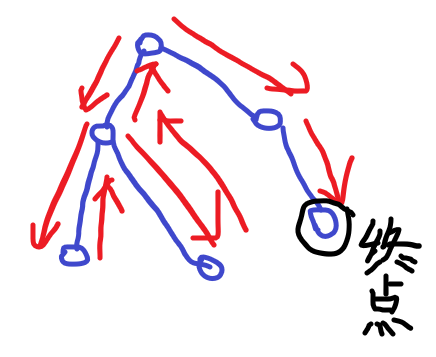
答案就是少了从出发点到结束点的路径长度。因此选定起点后的花费=2*(整棵树边权和)-dis(起点,终点)
那么只需要最大化出发点到结束点的路径长度,就可以使得花费最小。
所以问题就转化成了,怎么在一棵树上,对每个点求离他最远的点与他的距离是多少。
如果只求一个点离他最远点的距离,显然一遍dfs可以解决问题,但是现在要求n个点,时间复杂度O(n^2)显然不能接受。
因此,想到了树的直径,想想我们是怎么求树的直径的,①先随便选择一个点dfs,找到距离他最远的那个点。②从找到的这个点出发dfs,再找到距离他最远的点,这两个点就是树的直径的两个端点。
这样有一个很显然的性质,对于树上的每个节点,距离他最远的点一定是树的直径的某一个端点,因此要知道每个点距离他最远的点距离是多少,只需要先得到树的直径的两个端点,然后以这两个端点为根2遍dfs预处理出每个点分别到这两个端点的距离即可。
代码
/****************************
* Author : W.A.R *
* Date : 2020-09-01-21:11 *
****************************/
/*
牛客小白月赛27 A
https://ac.nowcoder.com/acm/contest/6874/A
树的直径
求n个点,距离其最远的点与其的距离
正常是n^2做法,利用树的直径的性质把时间复杂度优化到 O(3*n)
*/
#pragma GCC optimize("O3")
#pragma G++ optimize("O3")
#include<stdio.h>
#include<string.h>
#include<math.h>
#include<iostream>
#include<algorithm>
#include<queue>
#include<map>
#include<stack>
#include<string>
#include<set>
#define mem(a,x) memset(a,x,sizeof(a))
#define Rint register int
using namespace std;
typedef long long ll;
const int maxn=1e6+10;
const ll mod=1e9+7;
namespace Fast_IO{
const int MAXL((1 << 18) + 1);int iof, iotp;
char ioif[MAXL], *ioiS, *ioiT, ioof[MAXL],*iooS=ioof,*iooT=ioof+MAXL-1,ioc,iost[55];
char Getchar(){
if (ioiS == ioiT){
ioiS=ioif;ioiT=ioiS+fread(ioif,1,MAXL,stdin);return (ioiS == ioiT ? EOF : *ioiS++);
}else return (*ioiS++);
}
void Write(){fwrite(ioof,1,iooS-ioof,stdout);iooS=ioof;}
void Putchar(char x){*iooS++ = x;if (iooS == iooT)Write();}
inline int read(){
int x=0;for(iof=1,ioc=Getchar();(ioc<'0'||ioc>'9')&&ioc!=EOF;)iof=ioc=='-'?-1:1,ioc=Getchar();
if(ioc==EOF)exit(0);
for(x=0;ioc<='9'&&ioc>='0';ioc=Getchar())x=(x<<3)+(x<<1)+(ioc^48);return x*iof;
}
inline long long read_ll(){
long long x=0;for(iof=1,ioc=Getchar();(ioc<'0'||ioc>'9')&&ioc!=EOF;)iof=ioc=='-'?-1:1,ioc=Getchar();
if(ioc==EOF)exit(0);
for(x=0;ioc<='9'&&ioc>='0';ioc=Getchar())x=(x<<3)+(x<<1)+(ioc^48);return x*iof;
}
template <class Int>void Print(Int x, char ch = '�'){
if(!x)Putchar('0');if(x<0)Putchar('-'),x=-x;while(x)iost[++iotp]=x%10+'0',x/=10;
while(iotp)Putchar(iost[iotp--]);if (ch)Putchar(ch);
}
void Getstr(char *s, int &l){
for(ioc=Getchar();ioc==' '||ioc=='
'||ioc==' ';)ioc=Getchar();
if(ioc==EOF)exit(0);
for(l=0;!(ioc==' '||ioc=='
'||ioc==' '||ioc==EOF);ioc=Getchar())s[l++]=ioc;s[l] = 0;
}
void Putstr(const char *s){for(int i=0,n=strlen(s);i<n;++i)Putchar(s[i]);}
} // namespace Fast_IO
using namespace Fast_IO;
struct Edge{int nxt,to,w;}e[maxn];
int head[maxn],ct,maxi;ll cost[maxn],dis1[maxn],dis2[maxn],maxx;
void addE(int u,int v,int w){e[++ct].to=v;e[ct].w=w;e[ct].nxt=head[u];head[u]=ct;}
void dfs(int u,int fa,ll dep,int flag){
if(dep>maxx){maxx=dep;maxi=u;}
if(flag==1)dis1[u]=dep;else if(flag==2)dis2[u]=dep;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;if(v==fa)continue;
dfs(v,u,dep+e[i].w,flag);
}
}
int main(){
int n=read();ll m=read_ll();ll sum=0;
for(int i=1;i<n;i++){int u=read(),v=read(),w=read();addE(u,v,w);addE(v,u,w);sum+=w;}
maxx=0,maxi=0;dfs(1,1,0,0);
maxx=0;dfs(maxi,maxi,0,1);
maxx=0;dfs(maxi,maxi,0,2);
for(int i=1;i<=n;i++)cost[i]=sum*2-max(dis1[i],dis2[i]);
sort(cost+1,cost+1+n);ll now=0;int cnt=0;
for(int i=1;i<=n;i++){now+=cost[i];cnt++;if(now>m){cnt--;break;}}
printf("%d
",cnt);
return 0;
}
乱七八八糟
写这篇博客就是觉得这道问题处理的思想非常巧妙,也许在以后遇到的树的问题可以有借鉴意义,所以就写下来啦,就很开心啦~