应用层级时空记忆模型(HTM)实现对实时异常流时序数据检测
Real-Time Anomaly Detection for Streaming Analytics
Subutai Ahmad SAHMAD@NUMENTA.COM
Numenta, Inc., 791 Middlefield Road, Redwood City, CA 94063 USA
Scott Purdy SPURDY@NUMENTA.COM
Numenta, Inc., 791 Middlefield Road, Redwood City, CA 94063 USA
摘要
世界上的许多数据都是流式的时间序列数据,在这些数据中,异常在关键情况下提供了重要的信息。然而,检测流式数据中的异常是一项艰巨的任务,需要探测器实时处理数据,并在进行预测的同时学习。本文提出了一种新的基于在线序列记忆算法的异常检测技术——分层时间记忆(HTM)。我们展示了一个实时检测财务指标异常的实时应用程序的结果。我们还在NAB上对算法进行了测试,NAB是一个发布的实时异常检测基准,我们的算法在NAB上取得了最好的结果。
一、概述
在每个行业中,我们都看到流媒体形式的时间序列数据的可用性呈指数级增长。 在物联网(IoT)和连接的实时数据源的兴起的推动下,我们现在拥有大量带有传感器的应用程序,可以生成重要且不断变化的数据。
实时流数据中的异常检测在许多行业中具有实际和重要的应用。 异常检测有许多用例,包括预防性维护,防欺诈,故障检测和监控。 用例可以在许多行业中找到,例如金融,IT,安全,医疗,能源,电子商务和社交媒体。
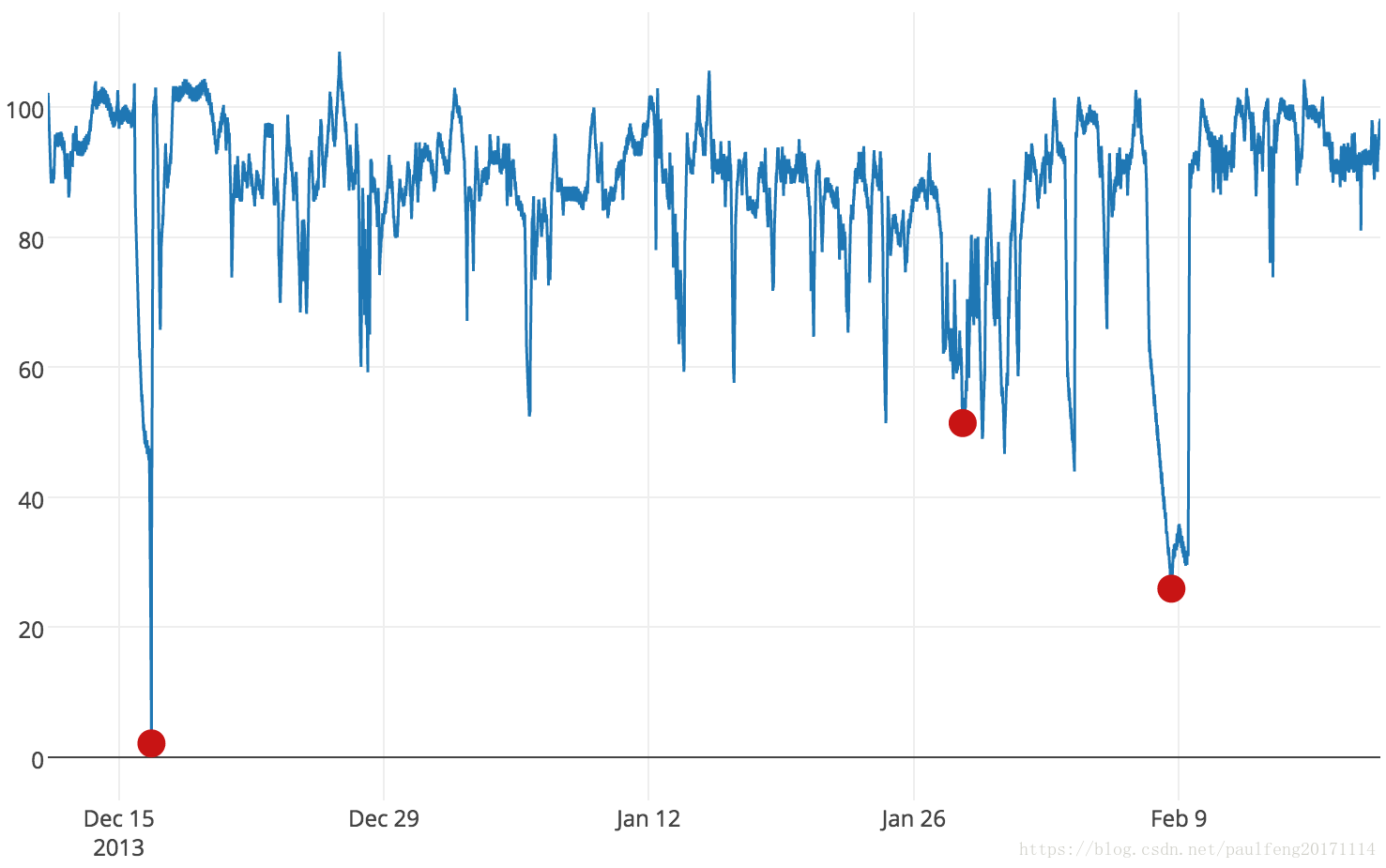
我们将异常定义为系统行为异常且与过去行为明显不同的时间点。 根据这个定义,异常并不一定意味着问题。 改变可能是由于负面原因,例如发动机上的温度传感器上升,表明可能即将发生故障。 或者更改可能是出于积极的原因,例如新产品页面上的网页点击异常高,显示需求强劲。 无论哪种方式,数据都是不寻常的,可能需要采取行动。 异常可以是空间的,意味着该值超出了典型范围,如图1中的第一个和第三个异常。它们也可以是时间的,其中值不在典型范围之外,但它发生的顺序是不寻常的。 图1中的中间异常是时间异常。
图1.该图显示了来自大型工业机器内部组件的实际温度传感器数据。 异常用红色圆圈标记。 第一个异常是计划停工。 第三个异常是灾难性的系统故障。 第二个异常,一个微妙但可观察到的行为变化,表明问题的实际发生导致最终的系统故障。
实时应用程序对机器学习施加了自己独特的限制。 流应用中的异常检测特别具有挑战性。 检测器必须处理数据并实时输出决策,而不是通过批量文件进行多次传递。 在大多数情况下,传感器流的数量很大,人类很少有机会,更不用说专家干预了。 因此,以无人监督的自动方式(例如,无需手动参数调整)操作通常是必要的。 底层系统通常是非平稳的,探测器必须不断学习和适应不断变化的统计数据,同时进行预测。
本文的目的是介绍一种专为此类实时应用而设计的新型异常检测技术。 我们将展示如何使用Hierarchical Temporal Memory (HTM)网络(Hawkins&Ahmad,2016; Padilla等,2013; Rozado等,2012)以有原则的方式在各种条件下稳健地检测异常。 由此产生的系统是高效的,非常容忍噪声数据,不断适应数据统计的变化,并检测非常微妙的异常,同时最大限度地减少误报。 我们展示了实时金融异常检测应用程序的定性示例。 我们还报告了实时异常检测的开放基准测试的领先结果。 该算法已经商业化部署,我们将讨论从这些部署中学到的一些实践经验教训。 我们已经在开源存储库中提供了完整的源代码(包括最终应用程序代码)。
二、有关工作
时间序列中的异常检测是一个研究很多的领域,可追溯到(Fox,1972)。 一些技术,如基于分类的方法,受到监督或半监督。 虽然标记数据可用于改善结果,但监督技术通常不适用于异常检测(G¨ornitz等,2013)。 图2说明了对连续学习的需求,这通常不是可以使用监督算法。
图2. Amazon EC2实例的CPU利用率(百分比)。 对计算机上运行的软件进行更改会导致CPU使用率发生变化。 持续学习对于像这样对流数据执行异常检测至关重要。
其他技术,如简单阈值,聚类和指数平滑,只能检测空间异常。 Holt-Winters是后者的一个例子,通常用于商业应用(Szmit&Szmit,2012)。 在实践中通常使用的是变点检测方法,其能够识别时间异常。 典型的方法是在两个独立的移动窗口中对时间序列进行建模,并检测时间序列度量中何时存在显着偏差(Basseville&Nikiforov,1993)。 这些方法通常计算速度极快且内存开销较低。 这些统计技术的检测性能可能对窗口和阈值的大小敏感。 随着数据的变化,这有时会导致许多误报,需要频繁更新阈值,以便在最小化误报的同时检测异常。
Skyline项目提供了许多统计技术的开源实现,用于检测流数据中的异常(Stanway,2013)。 不同的算法可以组合成一个整体。 Skyline算法包含在我们的结果中。
还有其他算法能够检测复杂场景中的时间异常。 ARIMA是一种用于对季节性时态数据建模的通用技术(Bianco等,2001)。 它可以有效地检测具有常规每日或每周模式的数据异常。 它不能动态地确定季节性的时期,尽管已经开发了这样做的延伸(Hyndman&Khandakar,2008)。 还研究了将ARIMA应用于多变量数据的技术(Tsay,2000)。 贝叶斯变换点检测方法是分割时间序列的自然方法,可用于在线异常检测(Adams&Mackay,2007; Tartakovsky等,2013)。 用于流数据的通用异常检测的一些附加技术包括(Keogh等人,2005; Rebbapragada等人,2009)。
雅虎发布了用于时间序列异常检测的开源EGADS框架,该框架将时间序列预测技术与常见的异常检测算法结合起来(Laptev等,2015)。 Twitter发布了自己的时间序列数据开源异常检测算法(Kejariwal,2015)。 两者都能够检测空间和时间异常。 我们的结果中包含了与Twitter检测软件的实证比较。
已经有许多基于模型的方法应用于特定领域。 这些往往对他们建模的领域非常具体。 示例包括飞机发动机测量中的异常检测(Simon&Rinehart,2015),云数据中心温度(Lee等人,2013)和ATM欺诈检测(Klerx等人,2014)。 虽然这些方法可能在特定域中取得成功,但它们不适用于通用应用程序。
我们已经回顾了一些与我们的工作最相关的算法。 全面的文献综述超出了本文的范围,但是有一些关于异常检测技术的详细综述可供进一步阅读(Chandola等,2009; Hodge&Austin,2004; Chandola等,2008)。
在本文中,我们专注于使用分层时间记忆(HTM)分层时间记忆(HTM)进行异常检测。 HTM是一种源自神经科学的机器学习算法,它模拟流数据中的空间和时间模式(Hawkins&Ahmad,2016; Rozado等,2012)。 HTM与序列预测中的一些现有算法相比是有利的,特别是复杂的非马尔可夫序列(Cui等,2015; Padilla等,2013)。 HTM不断学习系统,自动适应不断变化的统计数据,这是一种与流分析特别相关的属性。
三、使用HTM实现异常检测
典型的流应用涉及分析实时发生的连续数据流。 此类应用包含一些独特的挑战。 我们将此形式化如下。 设矢量xtxt表示时刻tt的实时系统的状态。 该模型接收连续的输入流:
(1)
例如,考虑监控数据中心的任务。的组件可能包括各种服务器的CPU使用率,带宽测量值,服务请求的延迟等。在每个时间点tt,我们希望确定系统的行为是否异常。 关键挑战之一是必须实时地进行确定,即在时间t+1t+1之前并且没有任何前瞻。 在实际应用中,系统的统计数据可以动态变化。 例如,在生产数据中心,可能会随时安装软件升级,从而改变系统的行为(图2)。 模型的任何重新训练必须在时间t+1t+1之前在线完成。最后,各个测量不是独立的,并且包含可以被利用的重要时间模式。
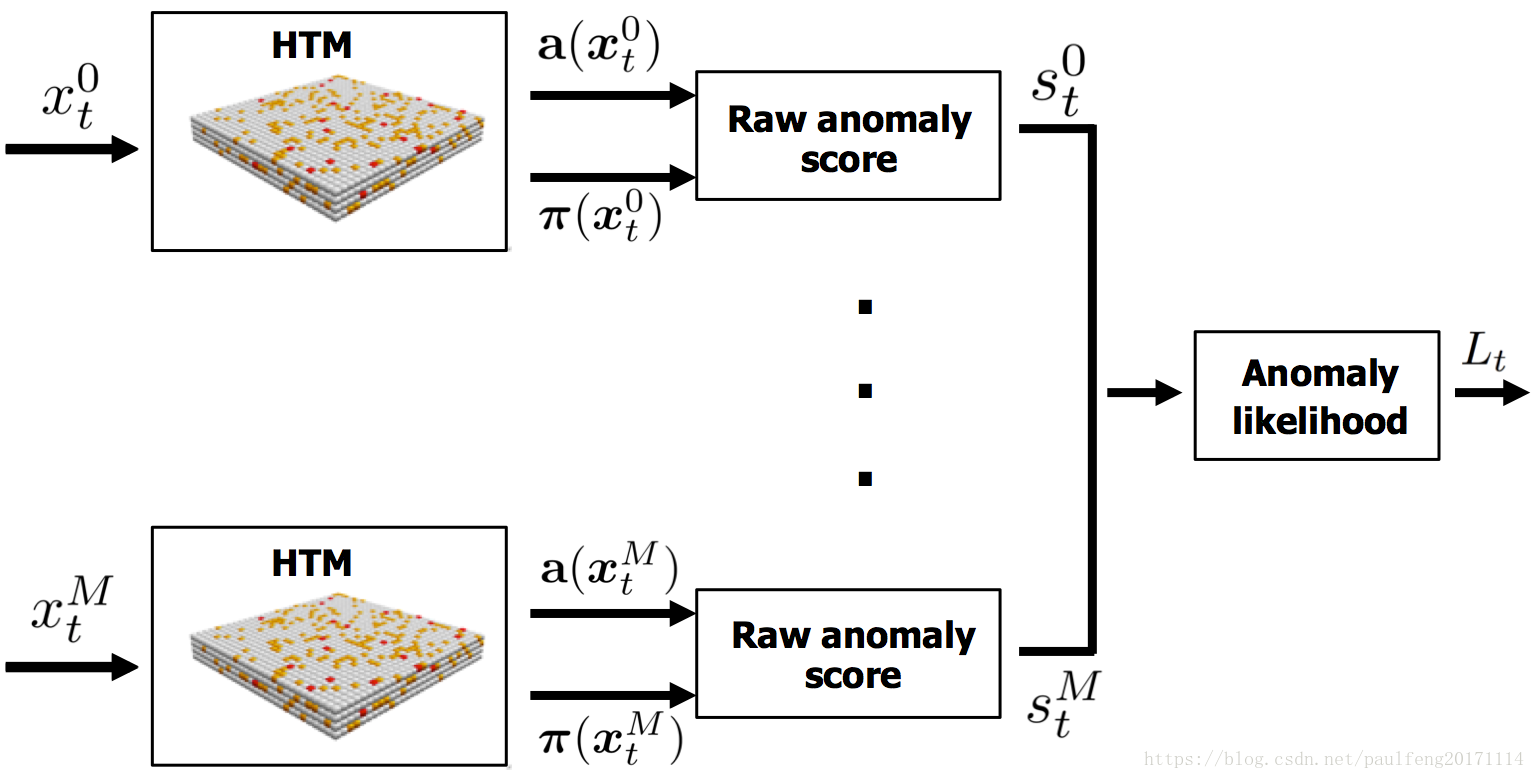
HTM是一种似乎与上述约束相匹配的学习算法。 HTM网络不断学习和模拟其输入的时空特征。 HTM已被证明可以很好地用于预测任务(Cui等,2015; Padilla等,2013),但HTM网络不直接输出异常分数。为了执行异常检测,我们利用HTM中可用的两种不同的内部表示。给定输入xtxt,向量a(xt)a(xt)是表示当前输入的稀疏二进制代码。我们还利用内部状态向量π(xt)π(xt)表示对a(xt+1)a(xt+1)的预测,即对下一个输入的预测。预测向量包含关于当前序列的推断信息。特别地,给定输入将导致不同的预测,这取决于当前检测到的序列和序列内输入的当前推断位置。预测的质量取决于HTM对当前数据流建模的程度。有关这些表示的更详细说明,请参阅(Hawkins&Ahmad,2016)。
a(xt)a(xt)和π(xt)π(xt)在每次迭代时重新计算,但不直接表示异常。 为了创建一个强大的异常检测系统,我们引入了两个额外的步骤。 我们首先从两个稀疏向量计算原始异常分数(rawanomalyscore)原始异常分数(rawanomalyscore)。 然后,我们计算一个异常似然值(anomalylikelihood)异常似然值(anomalylikelihood),该阈值被阈值化以确定系统是否是异常的。 图3显示了我们的算法的框图。 这两个步骤详述如下。 然后,我们将描述如何稳健地处理由多个不同模型组成的更大系统。
图3.算法中的主要功能步骤。
3.1计算原始异常分数(raw anomaly score)
我们计算一个原始异常分数,用于衡量模型预测输入与实际输入之间的偏差。 它是根据预测稀疏矢量和实际稀疏矢量之间的交集来计算的。 在时间tt,原始异常分数stst给出为:
(2)
如果当前输入被完美预测,则原始异常分数将为0;如果完全不可预测,则原始异常分数将为1,或者取决于输入和预测之间的相似性,原始异常分数将介于两者之间。
该评分的一个有趣方面是正确处理分支序列。 在HTM中,多个预测以π(xt)π(xt)表示为每个单独预测的二元并集。 与Bloom过滤器类似,只要向量足够稀疏且具有足够的维度,就可以同时表示中等数量的预测,并且指数上的误差几率很小(Bloom,1970; Ahmad&Hawkins,2016)。 异常分数在以下意义上优雅地处理分支序列。 如果两个完全不同的输入都是可能的和预测的,接收任一输入将导致0异常分数。 任何其他输入将产生正异常分数。
由于HTM的持续学习性质,也可以优雅地处理对底层系统的更改。 如果系统的行为发生变化,则异常分数在移位点处会很高,但在模型适应“新常态”时会自动降级为零。 除了基础度量值的空间移位之外,还处理系统的时间特性的变化。 (有关示例,请参阅结果部分。)
3.2计算异常似然值(anomaly likelihood)
上述原始异常分数表示当前输入流的可预测性的瞬时度量。 这适用于可预测的场景,但在许多实际应用中,底层系统本质上是噪声和不可预测的。 在这些情况下,通常可预测性的变化表明了无意义的行为。 例如,请考虑图4.此数据显示负载均衡器在生产网站上提供HTTP请求时的延迟。 尽管延迟通常较低,但偶尔出现随机跳跃并且异常得分相应的峰值并不罕见。 直接对原始异常分数进行阈值处理会导致许多误报。 然而,如图的后半部分所示,高延迟请求频率的持续增加是不寻常的,因此报告为异常。
图4.非常嘈杂,不可预测的流。 数据显示生产网站上负载均衡器的延迟(以秒为单位)。 红点表示延迟异常增加的大致位置。
为了处理这类场景,我们引入了第二步。 我们不是直接对原始分数进行阈值处理,而是对异常分数的分布进行建模,并使用此分布来检查当前状态是否异常的可能性。 因此,异常可能性是定义当前状态如何基于HTM模型的预测历史异常的度量。 为了计算异常可能性,我们维持最后W原始异常分数的窗口。 我们将分布建模为滚动正态分布,其中样本均值和方差从先前的异常分数不断更新,如下所示:
(3)
(4)
然后我们计算最近的异常分数的短期平均值,并对高斯尾概率(Q函数,(Karagiannidis&Lioumpas,2007))应用阈值来决定是否声明异常2。 我们将异常可能性定义为尾部概率的补充:
(5)
其中:
(6)
这里W′W′是一个短期均线的窗口,其中W′<<WW′<<W。我们阈值LtLt如果它非常接近1报告异常,:
(7)
值得注意的是,此测试适用于异常分数的分布,而不适用于基础度量值xtxt的分布。 因此,相对于近期历史,它是衡量模型能够预测的程度的指标。 在干净的可预测场景中,LtLt的行为类似于stst。 在这些情况下,分数的分布将具有非常小的方差并且将以0为中心。任何尖峰将同样导致LtLt中的相应尖峰。然而,在具有一些固有随机性或噪声的情况下,方差将更宽并且stst的单个峰值不会导致LtLt显着增加,但会出现一系列峰值。 有趣的是,从狂野随机到完全可预测的情景也会引发异常现象。
由于阈值处理LtLt涉及阈值尾部概率,因此警报的数量存在固有的上限。 用ϵϵ非常接近0,不太可能得到概率远高于的警报。 这也对误报的数量施加了上限。 假设异常本身也非常罕见,我们希望真阳性与假阳性的比例始终处于健康范围内(见下面的结果)。
虽然我们使用HTM作为基础时间模型,但似然技术并不特定于HTM。 它可以与输出稀疏代码或标量异常分数的任何其他算法一起使用。 检测器的整体质量将取决于底层模型表示域的能力。
3.3结合多个独立模型实现大型系统
许多工业或复杂环境包含大量传感数据流。理论上,给定足够的资源,可以创建一个大的复杂模型,整个矢量流作为输入。在实践中,通常将大型系统分解为许多较小的模型。训练较小的模型更容易,因为训练和推理的复杂性比输入维度的大小线性增长快得多(Bishop,2006)。因此,将解决方案组合成一组较小的模型可以提高准确性并且更快地实现性能。然而,即使进行这样的分解,重要的是计算累积单个模型的结果的全局度量并且指示系统的那些部分是否处于异常状态。例如,考虑运行生产网站的数据中心。自动警报系统可能需要不断决定是否生成警报并可能唤醒随叫随到的工程师。
我们假设代表系统的输入被分解为MM个不同的模型。 设xmtxtm是第mm个模型在时间tt的输入,而smtstm是与每个模型相关的原始异常分数。 我们希望计算一个全局度量,指示系统中异常的总体可能性(参见图5)。
图5.说明具有多个独立模型的复杂系统的功能图。
一种可能的方法是估计联合分布P(s0t,⋯,sM−1t)P(st0,⋯,stM−1)并对尾部概率应用阈值。对联合分布进行建模可能具有挑战性,特别是在流式上下文中。 如果我们进一步假设模型是独立的,我们可以简化并估算:
(8)
鉴于此,我们的异常可能性版本可以计算为:
(9)
上述方法存在一个缺陷。 在实时动态场景中,系统某个部分的关键问题通常可以级联到其他区域。 因此,通常存在内置的随机时间延迟,这反过来导致各种模型中的异常分数之间的不同时间延迟(Kim等人,2013)。 例如,在不同模型中多个异常事件彼此接近发生的情况比单个模型中的单个事件更不可能和不寻常。 正是这些情况对于在复杂系统中检测和捕获是有价值的。
理想情况下,我们能够估计出可追溯到时间的异常分数的联合分布,即P(s0i−j,s1i−j,⋯,sM−2t,sM−1t)P(si−j0,si−j1,⋯,stM−2,stM−1)。 理论上,这将捕获所有依赖关系,但这比早期的联合概率更难估计。 或者,在系统拓扑相对清晰且受您控制的情况下,可以创建依赖关系的显式图,监视节点对之间的预期行为,并检测与这些期望相关的异常。 已经证明这种技术非常精确确定监测服务之间特定呼叫的网站中的异常(Kim et al。,2013)。 然而,在大多数应用中,这种技术也是不切实际的。 对各种依赖关系进行建模可能很困难,并且通常可以设置任意系统来创建该图。
我们希望系统能够快速计算,做出相对较少的假设,并且具有自适应性。 我们提出了一种简单的通用机制,通过修改公式(9)来处理多个模型。 合并一个平滑的时间窗口。 窗口机制允许系统结合尖峰,其可能性在时间上接近但不完全重合。 设G是高斯卷积核:
(10)
我们将此卷积应用于每个单独的模型以获得最终的异常可能性得分3:
(11)
和以前一样,如果组合异常可能性大于阈值LtLt,我们会检测到异常Lt≥1−ϵLt≥1−ϵ。公式(11)表示用于检测复杂实时流应用中的异常的原则但实用的方法4。 和以前一样,LtLt是间接测量,在每个模型的原始异常分数之上计算。 它反映了模型在特定时间点的潜在可预测性,并不直接模拟传感器测量本身。
3.4实际考虑的问题
单个模型场景中有三个参数:WW,W′W′和ϵϵ。 W是计算异常分数分布的持续时间。 系统性能对W不敏感,只要它足够大以计算可靠的分布。 数字W′W′控制异常分数的短期平均值。 在下面的所有实验中,我们使用W=8000W=8000和W′=10W′=10的宽大值。
参数ϵϵ也许是最重要的参数。 它控制异常报告的频率,以及误报和漏报之间的平衡。 在实践中我们发现了ϵ=10−5ϵ=10−5适用于各种领域。 直观地说,这应该代表每10,000条记录一次的误报。
多重模型场景引入了一个附加参数,即窗口宽度σσ。 这在某种程度上取决于域,但由于软高斯卷积,系统对此设置不是非常敏感。 在下面的所有实验中,σ=6σ=6。
计算效率对于实时应用程序非常重要。 在我们的实现中,每个模型在当前高端笔记本电脑上每个输入向量需要不到10毫秒。 并行运行多个模型的基于服务器的部署可以在高端服务器上运行大约5,000个模型。 该图假设每个输入每5分钟到达一次(因此5,000个模型中的每一个需要每5分钟输出一个分数)。 作为社区服务,我们已经将完整的源代码发布到算法以及服务器应用程序代码库作为开源5。 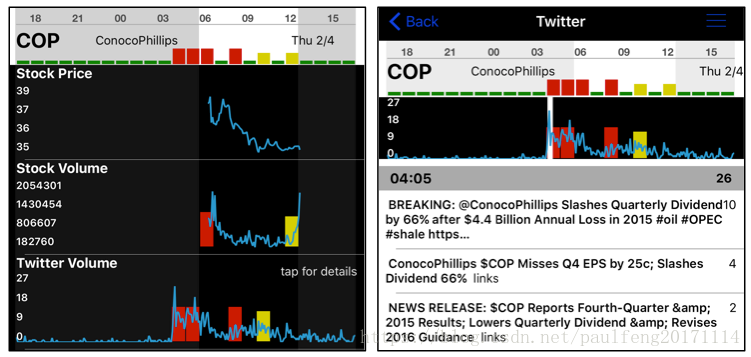
图6. 2016年2月4日的实时股票异常情况。
4结果
我们首先展示来自已部署应用程序的示例,该应用程序定性地演示了我们算法的行为。 然后,我们显示基准数据的定量结果。
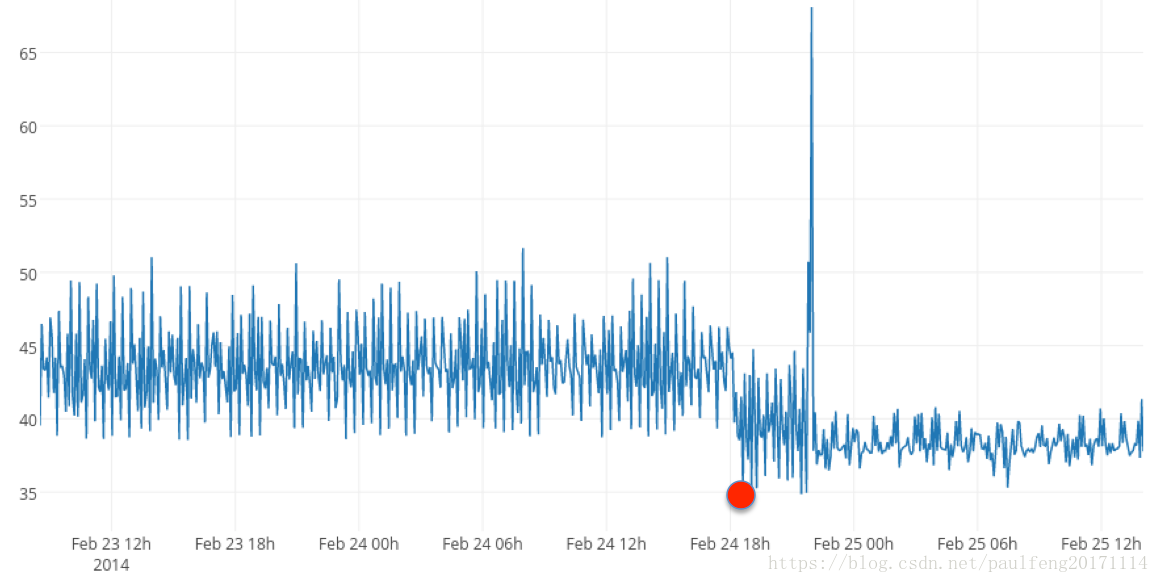
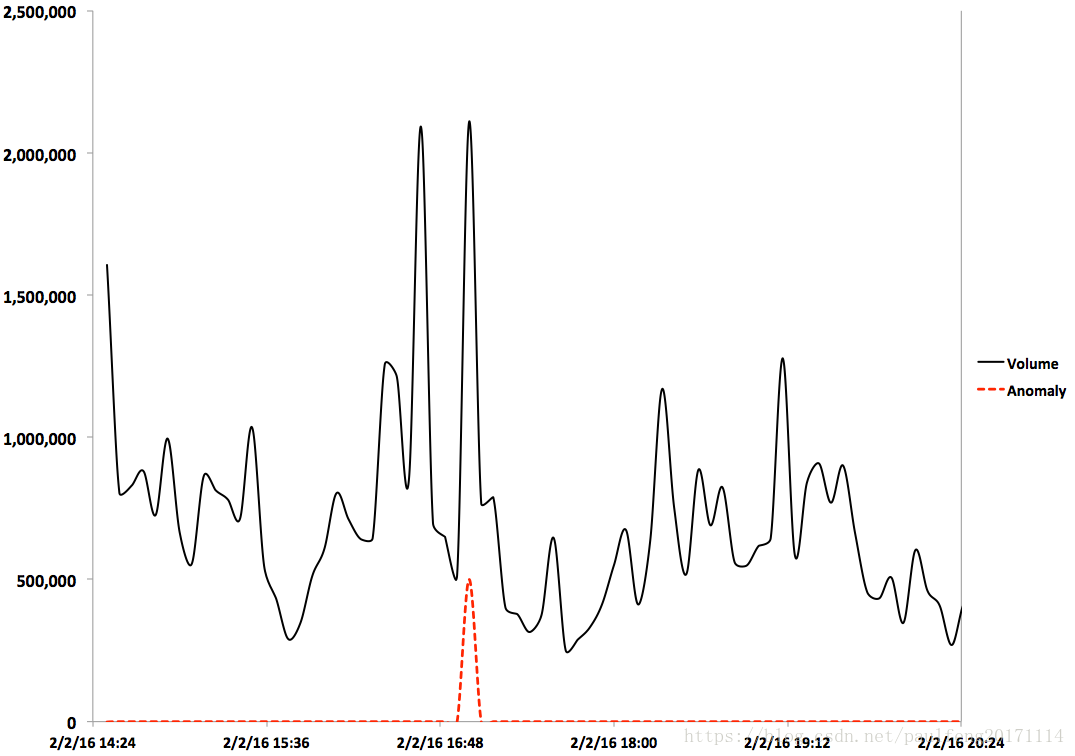
我们已将异常检测算法集成到实时产品中。该应用程序持续监控大量证券的大量金融和社交媒体指标,并在发生重大异常时实时提醒用户。图6显示了我们的应用程序的两个屏幕截图,它们向最终用户展示了实时异常检测的价值。在这个例子中,Twitter活动量的异常(与股息减少有关)在股价急剧下跌之前。 Twitter异常发生在市场开放之前。基础数据流非常嘈杂,许多重要的异常都是暂时的。图7显示了从我们的应用程序中提取的原始数据,展示了一个这样的异常。该图显示了Facebook几个小时的股票交易量。每个点代表五分钟的平均交易量。看到交易量出现飙升是正常的,但看到连续两次飙升是极不寻常的。因此,两个连续峰值表示该流中的时间异常。红色虚线表示我们的算法检测到异常的点,即Lt≥1−10−5Lt≥1−10−5的时间点。
图7. 2016年2月2日Facebook的股票交易量。红色虚线显示我们的算法检测到异常的点。 在这个流中,两个连续的尖峰是非常不寻常的并且代表异常。
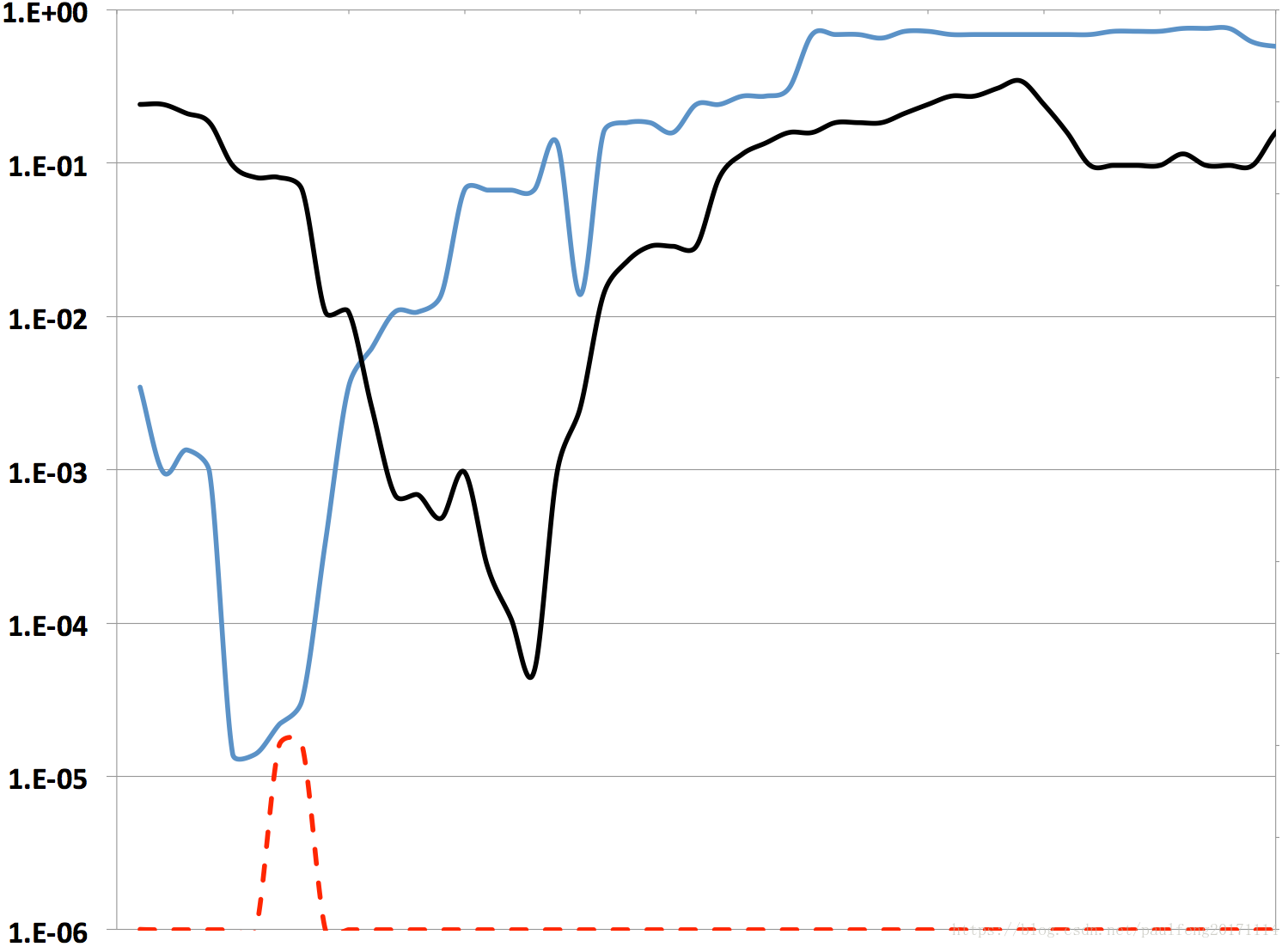
图8. 2016年2月4日两个Comcast指标得出的Q值。红色虚线表示我们的算法检测到异常的点。
图8显示了一个更详细的示例,演示了组合多个指标的价值。 两条实线表示与Comcast股票相关的两个独立指标的公式(5)中的Q值。 曲线越低,基础指标异常的可能性越大。 单独查看单个模型时,只有在其中一个值低于下方时才会检测到异常ϵ=10−5ϵ=10−5。 在这种情况下,不会检测到任何异常,因为任何一个都不会低于该值。 但是,如下降所示,两个指标都表现异常。 红色虚线表示基于我们的组合度量(公式(11))检测异常的结果。 因为蓝色曲线非常接近10−510−5,所以只要黑色曲线低于10−110−1,正确地合并两个指标就会标记异常。 从图表中可以理解,难以精确地排列两个度量,因此平滑时间窗口的值。
4.1真实基准数据的结果
以上部分展示了各个数据流的定性结果。 在本节中,我们提供定量基准测试结果。 NAB是一个包含58个流的基准测试,拥有超过350,000个来自各种不同应用程序的实时流数据记录(Lavin&Ahmad,2015)。 数据集标有异常。 每个数据文件的前15%保留用于自动校准。 NAB还包括一个围绕每个异常的窗口,并包含一个时间敏感的评分机制,有利于早期检测(只要检测在异常窗口内)。 “应用程序配置文件”定义了误报和漏报的权重,以说明错误检测较少或错误检测较少的情况。 该基准测试要求模型在所有流中使用一组参数来模拟实际部署中的自动化。
我们在NAB上运行了基于HTM的异常检测器。 表1包含我们的分数以及其他几种算法的分数,包括Etsy Skyline,Twitter AnomalyDetectionVec(ADVec)和贝叶斯在线变化点检测的变体(Adams&Mackay,2007)6。 我们包括“完美”探测器的分数,即理想化的探测器,它尽可能早地探测每个异常并且不产生误报。 我们还将“滑动阈值”和“随机”探测器的分数作为基线进行比较。 HTM探测器获得最佳总分,其次是Twitter ADVec和Etsy Skyline。 然而,从Perfect探测器的性能可以看出,基准测试具有挑战性,具有很大的未来改进空间。 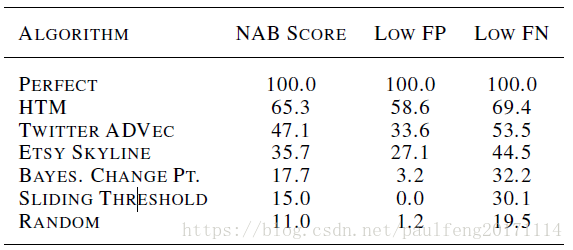
表1. NAB基准测试的性能。 第一列表示每种算法的标准NAB分数。 最后两列表示NAB的“偏低FP”和“偏低FN”曲线的分数,代表ROC曲线上的两个特定点。 为了进行比较,我们提供了一个“完美”探测器,一个不会出错的理想探测器。
NAB基准测试不测量明确的ROC曲线,但包括两个额外的“应用程序配置文件”,用于权衡误报和漏报之间的权重。 “奖励低FP”配置文件对误报应用较高的成本。 相反,“奖励低FN”配置文件对假阴性应用更高的成本。 表1的最后两列显示了这两个配置文件的分数。 尽管存在个体差异(特别是Twitter在“奖励低FN”列中显着改善),但我们的检测器整体表现最佳,表明它在假阳性和假阴性之间实现了良好的权衡。
仔细观察错误说明了实时应用程序中出现的一些有趣情况。 图9(a)展示了持续学习的价值。 此文件显示生产服务器上的CPU使用率随时间的变化并包含两个异常。 第一个是所有算法检测到的简单尖峰。 第二是使用的持续转变。 Skyline和HTM都检测到变化但随后适应新的法线(Skyline适应最快)。 然而,Twitter ADVec继续产生异常数日。 Skyline在这条小溪上得分最高。
图9.三个不同数据流的示例NAB结果。 形状对应于不同的检测器:HTM,Skyline和ADVec分别是菱形,方形和加号。 真正的阳性标记为黑色,误报标记为红色。 粉红色阴影区域表示NAB的异常窗口; 窗口内的任何检测都被视为真正的正面。
图9(b)和(c)显示了时间异常及其在早期检测中的重要性。 图9(b)是展示早期检测的示例。 所有三个探测器都检测到异常,但由于公制动态的细微变化,HTM在三小时前检测到它。 图9(c)显示了图1中所示的机器温度传感器数据的结果的特写。左侧的异常是稍微微妙的时间异常,其中时间行为是不寻常的但是个体读数在预期范围内。 这种异常(在2月8日发生灾难性故障之前)仅由HTM检测到。 尽管Skyline和HTM早于ADVec检测到它,但所有三个探测器都检测到右侧的异常。 在这个情节中,HTM和Skyline也都有误报。
我们选择这些例子是因为它们说明了在实践中发生的常见情况。 定性地,我们发现行为的时间变化通常先于较大的,易于检测的变化。 基于时间和序列的异常检测技术可以在流数据易于可见之前检测其中的异常。 我们推测图9(b)中的早期检测是由于HTM中的时间建模,因为较早的偏移很难通过纯空间手段来检测。 这使得希望这种算法可以用于生产中以提供早期警告,并且可能比空间技术更可靠地帮助避免问题。
贝叶斯变换点检测的低分是由于其对数据点的高斯或Gamma分布的强有力假设。 现实世界的流数据很混乱,并且这些假设在许多应用程序中都不成立。 在它确实存在的数据中(例如图2,9a),该算法工作良好,但对于大多数流(例如图1,4),它不能。 实际上,正是这种流媒体应用程序之间缺乏一致的分布导致我们对异常分数的分布进行建模而不是度量值的分布。
从计算效率的角度来看,在第一作者的笔记本电脑上,运行NAB的365,558条记录的完整数据集需要48分钟。 这表示每条记录平均为8毫秒。
5.讨论
随着连接的实时传感器的增加,流数据中的异常检测变得越来越重要。 这些用例涉及众多行业; 异常检测可能代表物联网中机器学习最重要的近期应用。
在本文中,我们讨论了一种用于实时流应用的新型异常检测算法。 基于HTM,该算法能够检测可预测区域和噪声区域中的空间和时间异常。 概率公式允许用户控制误报率,这是许多应用中的重要考虑因素。 我们讨论了具有多个独立模型的大型系统的扩展,这些模型包含时间窗口。
我们的结果表明,该算法可以在现实世界数据源的基准上获得最佳的结果。 我们的系统实用,因为它具有计算效率,可自动适应不断变化的统计数据,并且几乎不需要参数调整。 它目前在商业应用中使用,该算法的完整源代码可作为开源软件7使用。
(7Please see http://numenta.com/nab)
算法有许多可能的扩展。 NAB的误差分析表明,我们算法的误差不一定与其他两种算法的误差相关。 因此,基于集合的方法可以提供准确性的显着增加。 异常分数的高斯分布假设并不总是正确的。 探索其他分布代表另一种可能的扩展,可能会改善结果。
参考
References
Adams, Ryan Prescott and Mackay, David J. C. Bayesian Online Changepoint Detection. arXiv.org, pp. 7, 2007. doi: arXiv:0710.3742v1. URL http://arxiv.org/ abs/0710.3742.
Ahmad, Subutai and Hawkins, Jeff. How do neurons operate on sparse distributed representations? A mathematical theory of sparsity, neurons and active dendrites. pp. arXiv:1601.00720 [q–bio.NC], jan 2016. URL http: //arxiv.org/abs/1601.00720.
Basseville, M and Nikiforov, I V. Detection of Abrupt Changes, volume 2. 1993. Bianco, A. M., Garc´ıa Ben, M., Mart´ınez, E. J., and Yohai, V. J. Outlier detection in regression models with ARIMA errors using robust estimates. Journal of Forecasting, 20 (8):565–579, 2001.
Bishop, Christopher M. Pattern Recognition and Machine Learning, volume 4. Springer, 2006. ISBN 9780387310732.
Bloom, Burton H. Space/time trade-offs in hash coding with allowable errors, 1970. ISSN 00010782.
Chandola, V., Mithal, V., and Kumar, V. Comparative Evaluation of Anomaly Detection Techniques for Sequence Data. 2008 Eighth IEEE International Conference on Data Mining, pp. 743–748, 2008. ISSN 1550-4786. doi: 10.1109/ICDM.2008.151.
Chandola, Varun, Banerjee, A, and Kumar, V. Anomaly detection: A survey. ACM Computing Surveys (CSUR), (September):1–72, 2009.
Cui, Yuwei, Surpur, Chetan, Ahmad, Subutai, and Hawkins, Jeff. Continuous online sequence learning with an unsupervised neural network model. pp. arXiv:1512.05463 [cs.NE], 2015. URL http://arxiv.org/abs/1512.05463.
Fox, A J. Outliers in time series. Journal of the Royal Statistical Society, Series B (Methodological), 34(3):350–363, 1972. ISSN 00359246.
G¨ornitz, Nico, Kloft, Marius, Rieck, Konrad, and Brefeld, Ulf. Toward supervised anomaly detection. Journal of Artificial Intelligence Research, 46:235–262, 2013. ISSN 10769757. doi: 10.1613/jair.3623.
Hawkins, Jeff and Ahmad, Subutai. Why Neurons Have Thousands of Synapses, a Theory of Sequence Memory in Neocortex. Frontiers in Neural Circuits, 10(23):1–13, mar 2016. ISSN 1662-5110. doi: 10.3389/fncir.2016.00023.
URL http://journal.frontiersin.org/article/10.3389/fncir.2016.00023/abstract.
Hodge, Victoria J. and Austin, Jim. A survey of outlier detection methodologies, 2004. ISSN 02692821.
Hyndman, Rob J and Khandakar, Yeasmin. Automatic time series forecasting : the forecast package for R Automatic time series forecasting : the forecast package for R. Journal Of Statistical Software, 27(3):1–22, 2008.
Karagiannidis, George K. and Lioumpas, Athanaszsios S. An improved approximation for the Gaussian Q-function. IEEE Communications Letters, 11(8):644–646, 2007.
Kejariwal, Arun. Twitter Engineering: Introducing practical and robust anomaly detection in a time series [Online blog], 2015. URL http://bit.ly/1xBbX0Z.
Keogh, Eamonn, Lin, Jessica, and Fu, Ada. HOT SAX:Efficiently finding the most unusual time series subsequence. In Proceedings - IEEE International Conference on Data Mining, ICDM, pp. 226–233, 2005. ISBN 0769522785. doi: 10.1109/ICDM.2005.79.
Kim, Myunghwan, Sumbaly, Roshan, and Shah, Sam. Root cause detection in a service-oriented architecture. ACM International Conference on Measurement and Modeling of Computer Systems (SIGMETRICS ’13), pp. 93,2013. doi: 10.1145/2465529.2465753.
Klerx, Timo, Anderka, Maik, Buning, Hans Kleine, and Priesterjahn, Steffen. Model-Based Anomaly Detection for Discrete Event Systems. In 2014 IEEE 26th International Conference on Tools with Artificial Intelligence, pp. 665–672. IEEE, nov 2014. ISBN 978-1-4799-6572-4. doi: 10.1109/ICTAI.2014.105.
Laptev, Nikolay, Amizadeh, Saeed, and Flint, Ian. Generic and Scalable Framework for Automated Time-series Anomaly Detection. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 1939–1947. ACM, 2015.
Lavin, Alexander and Ahmad, Subutai. Evaluating Realtime Anomaly Detection Algorithms the Numenta Anomaly Benchmark. In 14th International Conference on Machine Learning and Applications (IEEE ICMLA’15), Miami, Florida, 2015. IEEE. doi: 10.1109/ICMLA.2015.141.
Lee, Eun Kyung, Viswanathan, Hariharasudhan, and Pompili,Dario. Model-based thermal anomaly detection incloud datacenters. Proceedings - IEEE International Conference on Distributed Computing in Sensor Systems,DCoSS 2013, pp. 191–198, 2013. doi: 10.1109/DCOSS.2013.8.
Padilla, Daniel E., Brinkworth, Russell, and McDonnell,Mark D. Performance of a hierarchical temporalmemory network in noisy sequence learning. In 2013 IEEE International Conference on Computational Intelligence and Cybernetics (CYBERNETICSCOM), pp. 45–51. IEEE, dec 2013. ISBN 978-1-4673-6053-1. doi:10.1109/CyberneticsCom.2013.6865779.
Rebbapragada, Umaa, Protopapas, Pavlos, Brodley,Carla E., and Alcock, Charles. Finding anomalous periodictime series : An application to catalogs of periodic variable stars. Machine Learning, 74(3):281–313, 2009.ISSN 08856125. doi: 10.1007/s10994-008-5093-3.
Rozado, David, Rodriguez, Francisco B., and Varona, Pablo. Extending the bioinspired hierarchical temporal memory paradigm for sign language recognition. Neurocomputing, 79:75–86, mar 2012. ISSN 09252312. doi:10.1016/j.neucom.2011.10.005.
Simon, Donald L and Rinehart, Aidan W. A Model-Based Anomaly Detection Approach for Analyzing Streaming Aircraft Engine Measurement Data. Technical Report 2015-218454, NASA, 2015.Stanway, A. Etsy Skyline, 2013. URL https://github.com/etsy/skyline.
Szmit, MacIej and Szmit, Anna. Usage of modified holtwinters method in the anomaly detection of network traffic:Case studies. Journal of Computer Networks and Communications, 2012, 2012. ISSN 20907141. doi:10.1155/2012/192913.
Tartakovsky, Alexander G., Polunchenko, Aleksey S., and Sokolov, Grigory. Efficient Computer Network Anomaly Detection by Changepoint Detection Methods. IEEE Journal of Selected Topics in Signal Processing, 7(1):4–11, feb 2013. ISSN 1932-4553. doi: 10.1109/JSTSP.2012.2233713. URL http://ieeexplore.ieee.org/lpdocs/epic03/wrapper.htm?arnumber=6380529.
Tsay, R. S. Outliers in multivariate time series. Biometrika, 87(4):789–804, dec 2000. ISSN 0006-3444. doi: 10.1093/biomet/87.4.789.