什么是网络流?
在生活中,什么比较像图呢?答案一定不少吧,其中我想举的例子就是水管了。水管相互之间都是连通的,会构成一张图。从供水的一端出发,水必然沿一个固定的方向流向最终的汇聚点,也就是有向图。同时,在条件的限制下,水管有粗有细,不同的水管单位时间内的流水量限制是不同的,可以看做是带权图。运输货物、限载限量、快递等等,是不是都很类似?我们称这样的带权、有向图为网络,因为有流量,即为网络流。具体定义就是,供应流量的出发点称为源点 S,接受流量的汇聚点称为汇点 T。比如下图就是一个网络,其中所标注的权值为这条边的容量——即可以流过的最大值。
2最大流
最大流是网络流中最常见的问题,我们先来定义什么是可行流:要求每条边上流过的值不超过它的容量,且在每个点、边都不允许有 “ 积水 ”,即源点出去的流量 = 汇点收到的流量。最大流是求在所有的可行流中,流动的 “ 水 ” (流量)最多有多少。这确实是一个比较实际的问题,因为比如在水管系统中,我们都希望在水管不会出现任何故障的情况下,能够流过最多的水。
之前提到的网络中,看上去的最大流应该是 24,就是流入汇点的最大容量。但实际上的最大流如下图所示(红色的数表示流量),应该是 23,具体需要用算法来求解这个问题,一个比较直观的解释就是,容量为 12、7 和 4 这三条边已经都满流了,无法再增加流量。
网络流的相关定义:
- 源点:有n个点,有m条有向边,有一个点很特殊,只出不进,叫做源点。
- 汇点:另一个点也很特殊,只进不出,叫做汇点。
- 容量和流量:每条有向边上有两个量,容量和流量,从i到j的容量通常用c[i,j]表示,流量则通常是f[i,j].
- 可行流:要求每条边上流过的值不超过它的容量,且在每个点、边都不允许有 “ 积水 ”,即源点出去的流量 = 汇点收到的流量。
- 最大流:是求在所有的可行流中,流动的 “ 水 ” (流量)最多有多少。这确实是一个比较实际的问题,因为比如在水管系统中,我们都希望在水管不会出现任何故障的情况下,能够流过最多的水。把源点比作工厂的话,问题就是求从工厂最大可以发出多少货物,是不至于超过道路的容量限制,也就是,最大流。
- 零流,即所有的流量都是0的流(显然是一个可行流)

求解思路:
- (1).我们就从这个零流开始考虑,假如有这么一条路,这条路从源点开始一直一段一段的连到了汇点,并且,这条路上的每一段都满足流量<容量,注意,是严格的<,而不是<=。
- (2).那么,我们一定能找到这条路上的每一段的(容量-流量)的值当中的最小值delta。我们把这条路上每一段的流量都加上这个delta,一定可以保证这个流依然是可行流,这是显然的。
- (3).这样我们就得到了一个更大的流,他的流量是之前的流量+delta,而这条路就叫做增广路。我们不断地从起点开始寻找增广路,每次都对其进行增广,直到源点和汇点不连通,也就是找不到增广路为止。
(4).当找不到增广路的时候,当前的流量就是最大流,这个结论非常重要。
补充:
-
(1).寻找增广路的时候我们可以简单的从源点开始做BFS,并不断修改这条路上的delta 量,直到找到源点或者找不到增广路。
-
(2).在程序实现的时候,我们通常只是用一个c 数组来记录容量,而不记录流量,当流量+delta 的时候,我们可以通过容量-delta 来实现,以方便程序的实现。
相关问题:
为什么要增加反向边?
在做增广路时可能会阻塞后面的增广路,
或者说,做增广路本来是有个顺序才能找完最大流的。
但我们是任意找的,为了修正,就每次将流量加在了反向弧上,让后面的流能够进行自我调整。
举例:
比如说下面这个网络流模型
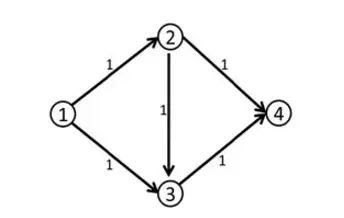
假如我们第一次找到了1-2-3-4这条增广路,这条路上的delta值显然是1。
于是我们修改后得到了下面这个流。(图中的数字是容量)
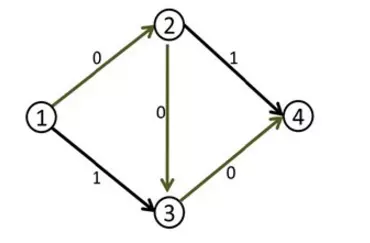
这时候(1,2)和(3,4)边上的流量都等于容量了,我们再也找不到其他的增广路了,当前的流量是1。
但是,
这个答案明显不是最大流,因为我们可以同时走1-2-4和1-3-4,这样可以得到流量为2的流。
那么我们刚刚的算法问题在哪里呢?
问题就在于我们没有给程序一个“后悔”的机会,应该有一个不走(2-3-4)而改走(2-4)的机制。
那么如何解决这个问题呢 ?
我们利用一个叫做反向边的概念来解决这个问题。即每条边(i,j)都有一条反向边(j,i),反向边也同样有它的容量。
我们直接来看它是如何解决的:
在第一次找到增广路之后,在把路上每一段的容量减少delta的同时,也把每一段上的反方向的容量增加delta。
c[x,y]-=delta;
c[y,x]+=delta;
我们来看刚才的例子,在找到1-2-3-4这条增广路之后,把容量修改成如下:

这时再找增广路的时候,就会找到1-3-2-4这条可增广量,即delta值为1的可增广路。将这条路增广之后,得到了最大流2。
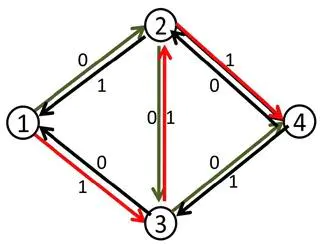
那么,这么做为什么会是对的呢?
事实上,当我们第二次的增广路走3-2这条反向边的时候,就相当于把2-3这条正向边已经是用了的流量给“退”了回去,不走2-3这条路,而改走从2点出发的其他的路也就是2-4。
如果这里没有2-4怎么办?
这时假如没有2-4这条路的话,最终这条增广路也不会存在,因为他根本不能走到汇点
同时本来在3-4上的流量由1-3-4这条路来“接管”。而最终2-3这条路正向流量1,反向流量1,等于没有流。