F. Tree with Maximum Cost（换根）

F. Tree with Maximum Cost

 

 

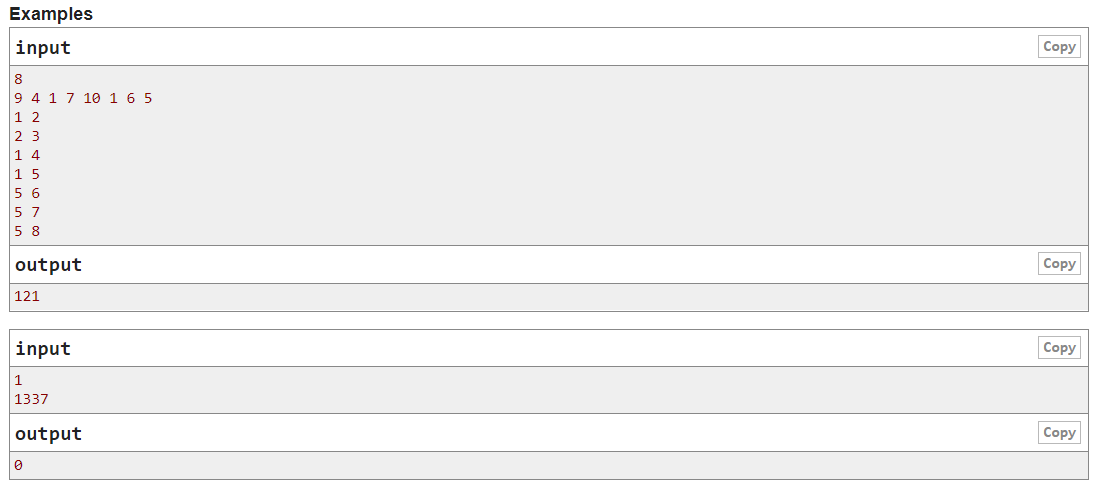
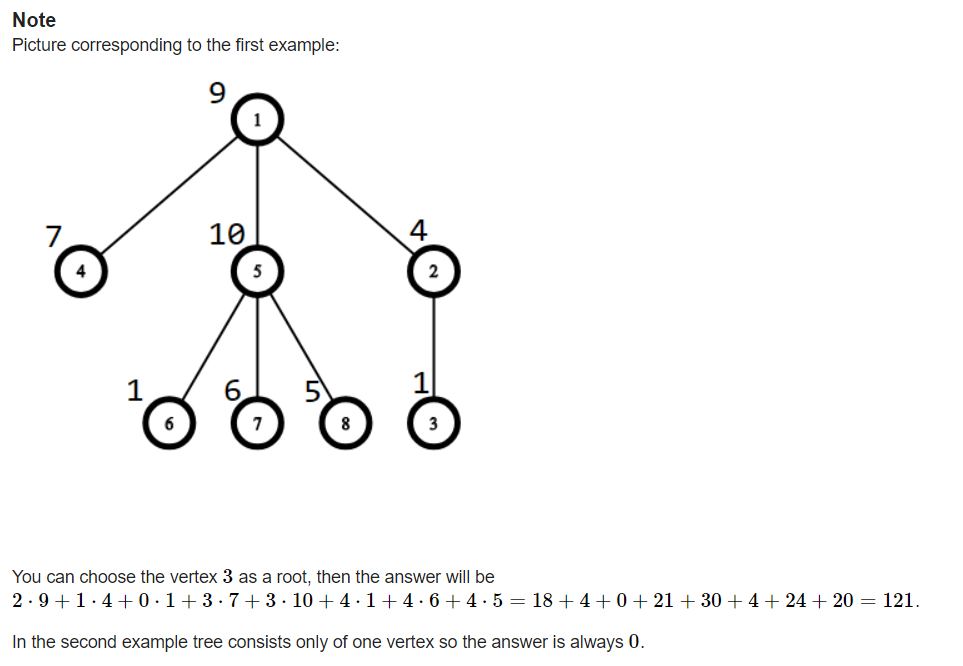
学习博客：https://blog.csdn.net/LJD201724114126/article/details/85240762?utm_source=app

题解：换根

我们先设sum[u] 等于 以u为根的子树的∑a_i (注意没有*距离），再计算以1为根的贡献值res。

这时我们要从父亲节点u向儿子节点v换根，故需要将res的值转化为以v为根的value

 

首先我们要先 res -= sum[v]，因为换根之前，以v为根的子树（包括v）到原根u的深度比换根之后，到新根v的深度少了一，故减去

然后我们sum[u] -= sum[v],因为原来sum[u]表示的是以u为根的值（包括了以v为根），而这时是以v为根的，故sum[u]要减去sum[v]，

res += sum[u]，因为换根之前，以u为根的子树（包括u）到原根u的深度比换根之后，到新根v的深度多了一，故加上

最后sum[v]+=sum[u]，因为v要成为整个树的根，而原来sum[v]不包括以u为根的节点值，故要加上。

换完之后我们再换回来。

这里巧妙的应用了换根，就是先求出任意一个根的结果，然后我们dfs，将相邻的根换一换，求出结果。

AC_Code

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 2e5+10;
const int inf=0x3f3f3f3f;
#define rep(i,first,last) for(ll i=first;i<=last;i++)
#define dep(i,first,last) for(ll i=first;i>=last;i--)
struct edge{ll to,nxt;}e[maxn<<1];
ll head[maxn<<1],cnt,a[maxn],n;
ll ans,res,sum[maxn];
void addedge(ll u,ll v){ e[++cnt].to=v; e[cnt].nxt=head[u];head[u]=cnt;}
void dfs1(ll u,ll fa,ll h){
    res+=(h*a[u]);
    sum[u]=a[u];
    for(ll i=head[u];i;i=e[i].nxt){
        ll v=e[i].to;
        if(v==fa) continue;
        dfs1(v,u,h+1);
        sum[u]+=sum[v];
    }
}
void dfs2(ll u,ll fa){
    ans=max(ans,res);
    for(ll i=head[u];i;i=e[i].nxt){
        ll v=e[i].to;
        if( v==fa ) continue;

        res-=sum[v];
        sum[u]-=sum[v];
        res+=sum[u];
        sum[v]+=sum[u];

        dfs2(v,u);

        sum[v]-=sum[u];
        res-=sum[u];
        sum[u]+=sum[v];
        res+=sum[v];
    }
    return ;
}
signed main()
{
    scanf("%lld",&n);
    rep(i,1,n) scanf("%lld",&a[i]);
    ll x,y;
    rep(i,1,n-1){
        scanf("%lld%lld",&x,&y);
        addedge(x,y);
        addedge(y,x);
    }
    dfs1(1,-1,0);
    dfs2(1,-1);
    printf("%lld
",ans);
    return 0;
}