吉哥系列故事——恨7不成妻:参考博客

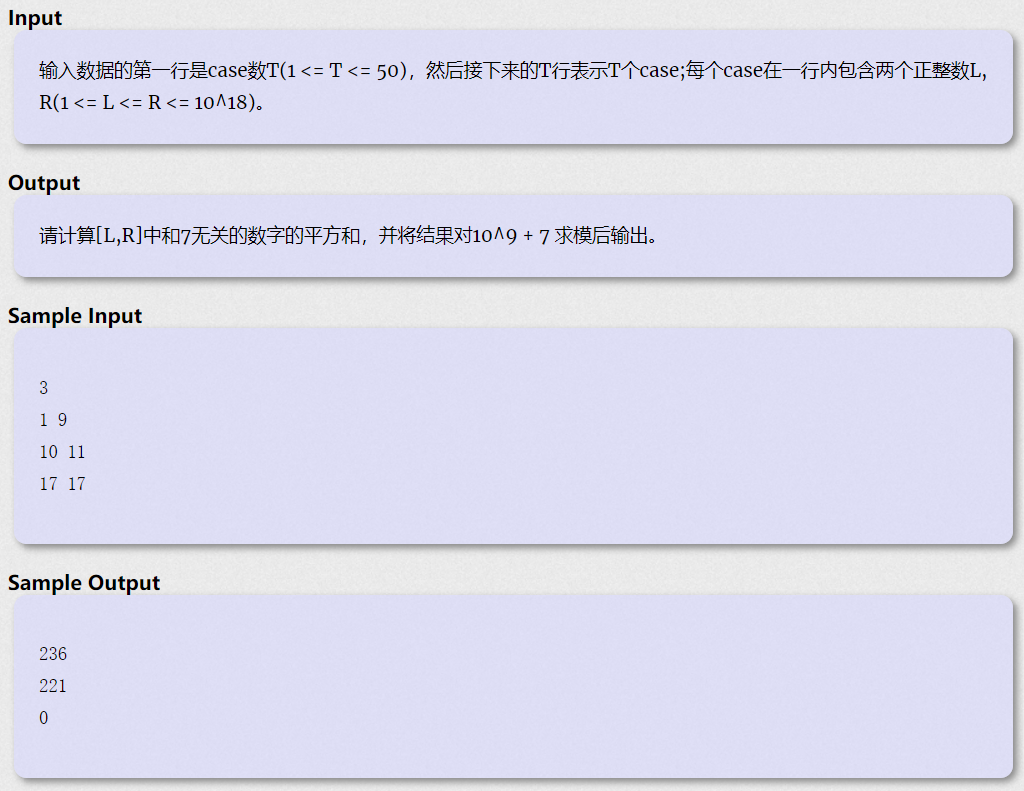
乍一看好像是道数位dp;然而要求的是平方和。
在暂时没有其他思路的情况下——能不能用数位dp做平方和?
数位dp在搜索的时候是这么个样子的:比如说
abcdefghi
现在搜到:
9982|e|fghi
那么现在确定了前面的9982,当前这一位和之后的 fghi 都不确定。
在这一位上的搜索结果就覆盖了efghi 所有的可行情况
那么很显然地,要求数的平方和也就是这个(9982efghi)的平方和
所以就是(998200000+efghi)的平方和。这个可以拆。
拆出来三个都可以求。
(998200000²想必不用多说;
2×998200000×efghi只需要知道sum(efghi),这个也好求;
efghi²呢?注意到这也是平方和,改变现在的问题让这个变成子问题就好了。)
现在这道题目被拆解为六块,分别是三个条件和三个返回值。
三个条件:
1.不能有某一位是7;
2.数位和不被7整除;
3.数不被7整除
对应的方法:
1.在枚举当前数位的时候直接跳过
if (i==7) continue;
2.传递数位和对7取模的余数sum
3.传递(当前确定下来的一部分)数对7取模的余数ori
if (!pos) ... sum && ori ...
三个值:
1.满足条件数的个数cnt
2.满足条件数的和sum
3.满足条件数的平方和sqsum
对应地,枚举令 pos 位置上的值为 i,有方程:
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <cstring> 5 #include <cmath> 6 #include <queue> 7 #include <stack> 8 #include <vector> 9 #include <set> 10 #include <map> 11 #include <sstream> 12 #include <algorithm> 13 using namespace std; 14 typedef long long ll; 15 const int maxn=20; 16 const ll mod=(ll)(1e9+7); 17 ll bit[maxn],tp[maxn]; 18 19 struct node{ 20 ll cnt; //满足条件数的个数 21 ll sum; //满足条件的数的和 22 ll sqsum; //满足条件的数的平方的和 23 node(ll _cnt=0,ll _sum=0,ll _sqsum=0):cnt(_cnt),sum(_sum),sqsum(_sqsum){} 24 }F[maxn][maxn][maxn]; 25 26 node dfs(int pos,int sum,int ori,bool lead,bool limit){ //枚举位置,每一位加起来的和%7,这个数%7,限制 27 //当pos==0时,当sum不是7的倍数,ori不是7的倍数时,上一层的数是合法的,个数记为1返回 28 //为什么返回的sum==0,sqsum==0呢?因为这是要返回上一层去算的 29 node ret, tmp; 30 if(!pos) return node((sum&&ori), 0, 0); 31 if(!limit && !lead && F[pos][sum][ori].cnt != -1) return F[pos][sum][ori]; 32 int endi=limit?bit[pos]:9; 33 tmp=node(0, 0, 0); 34 for (int i = 0; i <= endi; i ++) { 35 if(i == 7) continue; 36 ret = dfs(pos-1, (sum+i)%7, (ori*10+i)%7, lead&&!i, limit&&(i==endi)); 37 tmp.cnt = (tmp.cnt + ret.cnt) % mod; 38 tmp.sum = (tmp.sum + ret.sum + ret.cnt * i % mod * tp[pos-1] % mod) % mod; 39 tmp.sqsum = (tmp.sqsum + ret.sqsum + 2 * ret.sum % mod * i % mod * tp[pos-1] % mod) % mod; 40 tmp.sqsum = (tmp.sqsum + i * i * tp[pos-1] % mod * tp[pos-1] % mod * ret.cnt % mod) % mod; 41 } 42 return (!limit&&!lead) ? F[pos][sum][ori] = tmp: tmp; 43 } 44 45 ll solve(ll x){ 46 bit[0]=0; 47 while(x){ 48 bit[++bit[0]]=x%10; 49 x/=10; 50 } 51 return dfs(bit[0],0,0,1,1).sqsum; 52 } 53 54 int main() 55 { 56 memset(F,-1,sizeof(F)); 57 tp[0] = 1; 58 for (int i=1; i<=19; ++i) tp[i]=tp[i-1]*10 % mod; 59 int T; 60 scanf("%d", &T); 61 while (T--) { 62 long long L, R; 63 scanf("%lld%lld", &L, &R); 64 printf("%lld ", (solve(R) - solve(L-1) + mod) % mod); 65 } 66 return 0; 67 }