引用博客
【引入】
首先我们要清楚数位dp解决的是什么问题:
求出在给定区间 [A,B] 内,符合条件 f(i) 的数 i 的个数。条件 f(i) 一般与数的大小无关,而与数的组成有关
由于数是按位dp,数的大小对复杂度的影响很小
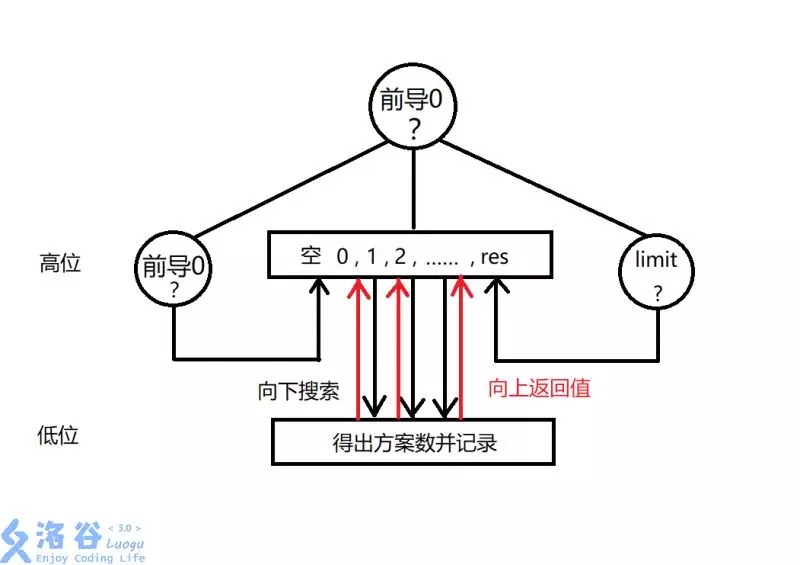
【设计搜索】
这里我们使用记忆化搜索实现数位dp。本质上记搜其实就是dp,下文会重点介绍dp值的使用和记录
一、记搜过程
从起点向下搜索,到最底层得到方案数,一层一层向上返回答案并累加,最后从搜索起点得到最终答案。
对于 [l,r] 区间问题,我们一般把他转化为两次数位dp,即找 [0,r] 和 [0,l-1] 两段,再将结果相减就得到了我们需要的 [l,r]
二、状态设计
如果理解了上述过程,我们需要考虑的就是怎样判断现在在哪一层,怎样判断当前的状态——这就需要我们传进一些参量。
dfs函数需要哪些参量?
-
首先是数位dp基本的量数字位数 pos ,记录答案的 st ,最高位限制 limit (这个后面会讲)
-
我们还需要一个判断判断前导0的标记 lead (这个后面也会讲)
-
由于数位dp解决的大多是数字组成问题,所以经常要比较当前位和前一位或前几位的关系(根据题意而定),所以一般在dfs()中也要记录前一位或前几位数 pre 方便比较。
-
除此之外还可以传进更多参量以区分状态,视题意而定。
数位dp的状态能记录的最好都记录上 ——lwz dalao
【细节分析】
一、前导0标记lead
由于我们要搜的数可能很长,所以我们的直接最高位搜起
举个例子:假如我们要从 [0,1000] 找任意相邻两数相等的数
显然 111,222,888 等等是符合题意的数
但是我们发现右端点 1000 是四位数
因此我们搜索的起点是 0000 ,而三位数的记录都是 0111,0222,0888 等等
而这种情况下如果我们直接找相邻位相等则 0000 符合题意而 0111,0222,0888 都不符合题意了
所以我们要加一个前导0标记
-
如果当前位 lead=1 而且当前位也是0,那么当前位也是前导0, pos+1 继续搜;
-
如果当前位 lead=1 但当前位不是0,则本位作为当前数的最高位, pos+1 继续搜;(注意这次根据题意st或其他参数可能发生变化)
当然前导 0 有时候是不需要判断的,上述的例子是一个有关数字结构上的性质,0会影响数字的结构,所以必须判断前导0;而如果我们研究的是数字的组成(例如这个数字有多少个 1 之类的问题),0并不影响我们的判断,这样就不需要前导0标记了。总之,这个因题而异,并不是必须要标记(当然记了肯定是不会出错的)
二、最高位标记limit
我们知道在搜索的数位搜索范围可能发生变化;
举个例子:我们在搜索 [0,555] 的数时,显然最高位搜索范围是 0 ~ 5 ,而后面的位数的取值范围会根据上一位发生变化:
-
当最高位是 1 ~ 4 时,第二位取值为 [0,9] ;
-
当最高位是 5 时,第二位取值为 [0,5] (再往上取就超出右端点范围了)
为了分清这两种情况,我们引入了limit标记:
-
若当前位 limit=1 而且已经取到了能取到的最高位时,下一位 limit=1 ;
-
若当前位 limit=1 但是没有取到能取到的最高位时,下一位 limit=0 ;
-
若当前位 limit=0 时,下一位 limit=0 。
我们设这一位的标记为 limit ,这一位能取到的最大值为 res ,则下一位的标记就是 i==res && limit ( i 枚举这一位填的数)
三、 {dp} 值的记录和使用
最后我们考虑dp数组下标记录的值
本文介绍数位dp是在记忆化搜索的框架下进行的,每当找到一种情况我们就可以这种情况记录下来,等到搜到后面遇到相同的情况时直接使用当前记录的值。
dp数组的下标表示的是一种状态,只要当前的状态和之前搜过的某个状态完全一样,我们就可以直接返回原来已经记录下来的dp值。
再举个例子
假如我们找 [0,123456] 中符合某些条件的数
假如当我们搜到 1000?? 时,dfs从下返上来的数值就是当前位是第 5 位,前一位是 0 时的方案种数,搜完这位会向上反,这是我们可以记录一下:当前位第 5 位,前一位是 0 时,有这么多种方案种数
当我们继续搜到 1010?? 时,我们发现当前状态又是搜到了第 5 位,并且上一位也是 0 ,这与我们之前记录的情况相同,这样我们就可以不继续向下搜,直接把上次的dp值返回就行了。
注意,我们返回的dp值必须和当前处于完全一样的状态,这就是为什么dp数组下标要记录 pos,pre 等参量了。
最重要的来了————————————————————
接着上面的例子,范围 [0,123456]
如果我们搜到了 1234?? ,我们能不能直接返回之前记录的:当前第 5 位,前一位是 4 时的dp值?
答案是否定的
我们发现,这个状态的dp值被记录时,当前位也就是第 5 位的取值是 [0,9] ,而这次当前位的取值是 [0,5] ,方案数一定比之前记录的dp值要小。
当前位的取值范围为什么会和原来不一样呢?
如果你联想到了之前所讲的知识,你会发现:现在的 limit=1 ,最高位有取值的限制。
因此我们可以得到一个结论:当 limit=1 时,不能记录和取用dp值!
类似上述的分析过程,我们也可以得出:当 lead=1 时,也不能记录和取用dp值!
p.s.当然没有这么绝对的说……因题而异的说……
以上就是计划搜索的完整步骤。
附图:
模板:
1 ll dfs(int pos,int pre,int st,……,int lead,int limit)//记搜 2 { 3 if(pos>len) return st;//剪枝 4 if((dp[pos][pre][st]……[……]!=-1&&(!limit)&&(!lead))) return dp[pos][pre][st]……[……];//记录当前值 5 ll ret=0;//暂时记录当前方案数 6 int res=limit?a[len-pos+1]:9;//res当前位能取到的最大值 7 for(int i=0;i<=res;i++) 8 { 9 //有前导0并且当前位也是前导0 10 if((!i)&&lead) ret+=dfs(……,……,……,i==res&&limit); 11 //有前导0但当前位不是前导0,当前位就是最高位 12 else if(i&&lead) ret+=dfs(……,……,……,i==res&&limit); 13 else if(根据题意而定的判断) ret+=dfs(……,……,……,i==res&&limit); 14 } 15 if(!limit&&!lead) dp[pos][pre][st]……[……]=ret;//当前状态方案数记录 16 return ret; 17 } 18 ll part(ll x)//把数按位拆分 19 { 20 len=0; 21 while(x) a[++len]=x%10,x/=10; 22 memset(dp,-1,sizeof dp);//初始化-1(因为有可能某些情况下的方案数是0) 23 return dfs(……,……,……,……);//进入记搜 24 } 25 int main() 26 { 27 scanf("%d",&T); 28 while(T--) 29 { 30 scanf("%lld%lld",&l,&r); 31 if(l) printf("%lld",part(r)-part(l-1));//[l,r](l!=0) 32 else printf("%lld",part(r)-part(l));//从0开始要特判 33 } 34 return 0; 35 }
例题:
【题意简述】
定义一个正整数的价值是把这个数的十进制写出来之后,最长的等差子串的长度。
求 [l,r][l,r] 范围内数字价值的总和。
【分析】
这道题很显然是一道数位dp,那么我们应该怎么样设计状态和转移呢?
数位位置,前一位数,等差数列共差是一定要记录的
我们还要把当前最大价值和整个数最大值也作为状态
dp过程见代码注释(数位dp主要还是套板子呀)
#include<bits/stdc++.h> using namespace std; typedef long long ll; int T,n,m,len,a[20]; ll l,r,dp[20][15][25][25][20]; ll dfs(int pos,int pre,ll st,ll sum,int d,int lead,int limit) //pos搜到的位置 //pre前一位数 //st当前公差最大差值 //sum整个数字的最大价值 //d共差 //lead判断是否有前导0 //limit判断是否有最高位限制 { if(pos>len) return sum;//dp结束 //记录状态(计划搜索) //注意d有负数,最小可以到-9,所以记录时数组下标是d+10 if((dp[pos][pre][st][sum][d+10]!=-1&&(!limit)&&(!lead))) return dp[pos][pre][st][sum][d+10]; ll ret=0; int res=limit?a[len-pos+1]:9;//最高位最大值 for(int i=0;i<=res;i++) { //有前导0且这位也是前导0,一切不变只有位数变化 if((!i)&&lead) ret+=dfs(pos+1,0,0,0,-38,1,limit&&(i==res)); //有前导0但这位不是前导0(这位是数字的最高位)开始有前一位,一个数形成等差数列 else if(i&&lead) ret+=dfs(pos+1,i,1,1,-38,0,limit&&(i==res)); //之前刚搜到1位还没有共差,两位数形成等差数列,记录共差 else if(d<-9) ret+=dfs(pos+1,i,2ll,2ll,i-pre,0,limit&&(i==res)); //搜到2位以后,共差若与前两位相同当前等差数列长度增加,若公差变化则更新整个数字的最大价值,等差数列长度又变为2 else if(d>=-9) ret+=dfs(pos+1,i,(i-pre==d)?st+1:2,max(sum,(i-pre==d)?st+1:2),(i-pre==d)?d:i-pre,0,limit&&(i==res)); } //没有前导0和最高限制时可以直接记录当前dp值以便下次搜到同样的情况可以直接使用。 return (!limit&&!lead)?dp[pos][pre][st][sum][d+10]=ret:ret; } ll part(ll x) { len=0; while(x) a[++len]=x%10,x/=10; memset(dp,-1,sizeof dp); return dfs(1,0,0,0,-38,1,1);//-38是随便赋的其实赋成-10就行了…… } int main() { scanf("%d",&T); while(T--) { scanf("%lld%lld",&l,&r); //l是0的时候要特别注意! printf("%lld ",l?(part(r)-part(l-1)):(part(r)-part(l)+1)); } return 0; }